Question 14. 3x2dy = (3xy + y2)dx
Solution:
We have,
3x2dy = (3xy + y2)dx
(dy/dx) = (3xy + y2)/3x2
It is a homogeneous equation,
So put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = (3xvx + v2x2)/3x2
v + x(dv/dx) = (3v + v2)/3
x(dv/dx) = [(3v + v2)/3] – v
x(dv/dx) = (3v + v2 – 3v)/3
3(dv/v2) = (dx/x)
On integrating both sides,
3∫(dv/v2) = ∫(dx/x)
-(3/v) = log|x| + c
-3x/y = log(x) + c (Where ‘c’ is integration constant)
Question 15. (dy/dx) = x/(2y + x)
Solution:
We have,
(dy/dx) = x/(2y + x)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = x/(2vx + x)
v + x(dv/dx) = 1/(2v + 1)
x(dv/dx) = [1/(2v + 1)] – v
x(dv/dx) = (1 – 2v2 – v)/(2v + 1)
(2v + 1)dv/(2v2 + v – 1) = -(dx/x)
On integrating both sides,
∫(2v + 1)dv/(2v2 + v – 1) = -∫(dx/x)
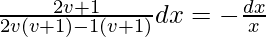
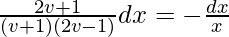
Solving by partial fraction,
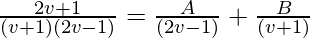
A(v + 1) + B(2v – 1) = (2v + 1) (i)
Putting v = -1 and solve above equation,
A(0) + B(-3) = (-1)
B = (1/3)
Putting v = -(1/2) and solve equation (i),
A(3/2) + B(0) = 2
A = (4/3)
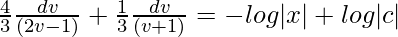
(3/2)log|2v – 1| + (1/3)log|v + 1| = -log|x| + log|c|
log|(2v – 1)2(v + 1)| = -log|x|3 + log|c|
|(2v – 1)2(v + 1)| = (c/x3)
(2y/x – 1)2(y/x + 1) = (c/x3)
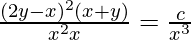
(2y – x)2(x + y) = c (Where ‘c’ is integration constant)
Question 16. (x + 2y)dx – (2x – y)dy = 0
Solution:
We have,
(x + 2y)dx – (2x – y)dy = 0
(dy/dx) = (x + 2y)/(2x – y)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = (x + 2vx)/(2x – vx)
v + x(dv/dx) = (1 + 2v)/(2 – v)
x(dv/dx) = [(1 + 2v)/(2 – v)] – v
x(dv/dx) = (1 + 2v – 2v + v2)/(2 – v)
(2 – v)dv/(1 + v2) = (dx/x)
On integrating both sides,
∫(2 – v)dv/(1 + v2) = ∫(dx/x)
2∫dv/(1 + v2) – ∫vdv/(1 + v2) = log|x| + log|c|
2tan-1v – (1/2)∫2vdv/(1 + v2) = log|x| + log|c|
2tan-1v – log|1 + v2|1/2 = log|cx|
2tan-1v = log|cx√(1 + v2)|
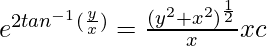
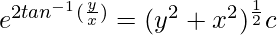 (Where ‘c’ is integration constant)
(Where ‘c’ is integration constant)
Question 17. 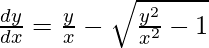
Solution:
We have,
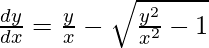
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = (vx/x) – √(v2x2/x2 – 1)
v + x(dv/dx) = v – √(v2 – 1)
x(dv/dx) = -√(v2 – 1)
dv/√(v2 – 1) = -(dx/x)
On integrating both sides,
∫dv/√(v2 – 1) = -∫(dx/x)
log|v + √(v2 – 1)| = -log|x| + log|c|
|v + √(v2 – 1)| = (c/x)
![Rendered by QuickLaTeX.com \frac{y}{x}-[\sqrt{(\frac{y}{x})^2-1}]x=c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dbfa75ef1e35753e68268a12909378fe_l3.png)
y + √(y2 – x2) = c (Where ‘c’ is integration constant)
Question 18. (dy/dx) = (y/x){log(y) – log(x) + 1}
Solution:
We have,
(dy/dx) = (y/x){log(y) – log(x) + 1}
(dy/dx) = (y/x){log(y/x) + 1}
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = v{log(v) + 1}
v + x(dv/dx) = vlog(v) + v
x(dv/dx) = vlog(v)
dv/vlogv = (dx/x)
On integrating both sides,
∫dv/vlogv = ∫(dx/x)
Let, logv = z
On differentiating both sides,
dv/v = dz
∫(dz/z) = ∫(dx/x)
log|z| = log|x| + log|c|
z = xc
log|v| = xc
log|y/x| = xc (Where ‘c’ is integration constant)
Question 19. (dy/dx) = (y/x) + sin(y/x)
Solution:
We have,
(dy/dx) = (y/x) + sin(y/x)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = v + sin(v)
x(dv/dx) = sin(v)
dv/sin(v) = (dx/x)
On integrating both sides,
∫dv/sin(v) = ∫(dx/x)
∫cosec(v)dv = ∫(dx/x)
log|tan(v/2)| = log(x) + log(c)
log|tan(y/2x)| = log|xc|
tan(y/2x) = |xc| (Where ‘c’ is integration constant)
Question 20. y2dx + (x2 – xy + y2)dy = 0
Solution:
We have,
y2dx + (x2 – xy + y2)dy = 0
(dy/dx) = -(y2)/(x2 – xy + y2)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = -(v2x2)/(x2 – xvx + v2x2)
v + x(dv/dx) = -(v2)/(1 – v + v2)
y(dv/dx) = [-(v2)/(1 – v + v2)] – v
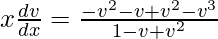
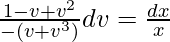
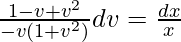
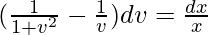
On integrating both sides,
∫dv/(1 + v2) – ∫dv/v = ∫(dx/x)
tan-1(v) – log(v) = log(x) + log(c)
tan-1(y/x) – log|y/x| = log(xc)
tan-1(y/x) = log|(y/x)xc|
tan-1(y/x) = log|yc|
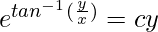 (Where ‘c’ is integration constant)
(Where ‘c’ is integration constant)
Question 21. [x√(x2 + y2) – y2]dx + xydy = 0
Solution:
We have,
[x√(x2 + y2) – y2]dx + xydy = 0
dy/dx = -[x√(x2 + y2) – y2]/xy
dy/dx = [y2 – x√(x2 + y2)]/xy
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = [v2x2 – x√(x2 + v2x2)]/xvx
v + x(dv/dx) = [v2 – √(1 + v2)]/v
x(dv/dx) = [v2 – √(1 + v2)]/v – v
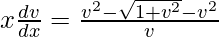
x(dv/dx) = -(√(1 + v2)/v
vdv/√(1 + v2) = -(dx/x)
On integrating both sides,
∫vdv/√(1 + v2) = -∫(dx/x)
(1/2)∫2vdv/√(1 + v2) = -∫(dx/x)
Let, 1 + v2 = z
On differentiating both sides,
2vdv = dz
(1/2)∫dz/√z = -∫(dx/x)
√z = -log|x| + log|c|
√(1 + v2) = log|c/x|
√(x2 + y2)/x = log|c/x|
√(x2 + y2) = xlog|c/x| (Where ‘c’ is integration constant)
Question 22. x(dy/dx) = y – xcos2(y/x)
Solution:
We have,
x(dy/dx) = y – xcos2(y/x)
(dy/dx) = y/x – cos2(y/x)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = v – cos2(v)
x(dv/dx) = -cos2(v)
dv/cos2(v) = -(dx/x)
On integrating both sides,
∫dv/cos2(v) = -∫(dx/x)
∫sec2vdv = -∫(dx/x)
tan(v) = -log|x| + log|c|
tan(y/x) = log|c/x| (Where ‘c’ is integration constant)
Question 23. (y/x)cos(y/x)dx – {(x/y)sin(y/x) + cos(y/x)}dy = 0
Solution:
We have,
(y/x)cos(y/x)dx – {(x/y)sin(y/x) + cos(y/x)}dy = 0
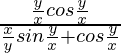
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
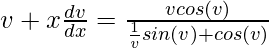
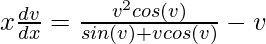
x(dv/dx) = (v2cosv – vsinv – v2cosv)/(sinv + vcosv)
x(dv/dx) = -vsinv/(sinv + vcosv)
On integrating both sides,
∫[(sinv + vcosv)/vsinv]dv = -∫(dx/x)
∫(dv/v) + ∫(cotv)dv = -∫(dx/x)
log|v| + log|sinv| = -log|x| + log|c|
log|vsinv| = log|c/x|
(y/x)sin(y/x) = (c/x)
ysin(y/x) = c (Where ‘c’ is integration constant)
Question 24. xylog(x/y)dx + {y2 – x2log(x/y)}dy = 0
Solution:
We have,
xylog(x/y)dx + {y2 – x2log(x/y)}dy = 0
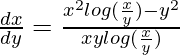
It is a homogeneous equation,
So, put x = vy (i)
On differentiating both sides w.r.t y,
dx/dy = v + y(dv/dy)
So,
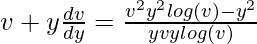
v + y(dv/dy) = (v2logv – 1)/(vlogv)
y(dv/dy) = [(v2logv – 1)/(vlogv)] – v
y(dv/dy) = (v2logv – 1 – v2logv)/vlogv
y(dv/dy) = -(1/vogv)
vlogvdv = -(dy/y)
On integrating both sides,
∫vlogvdv = -∫(dy/y)
logv∫vdv – ∫{d/dv(logv)∫vdv}dv}dv = -∫(dy/y)
(v2/2)logv – (1/2)∫(1/v)(v2/2)dv = -logy + logc
(v2/2)logv – (1/2)∫vdv = -logy + logc
(v2/2)logv – (v2/4) + logy = log|c|
(v2/2)[logv – 1/2] + logy = log|c|
v2[logv – (1/2)] + logy = log|c|
(x2/y2)[log(x/y) – (1/2)] + logy = log|c| (Where ‘c’ is integration constant)
Question 25. (1 + ex/y)dx + ex/y(1 – x/y)dy = 0
Solution:
We have,
(1 + ex/y)dx + ex/y(1 – x/y)dy = 0
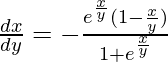
It is a homogeneous equation,
So, put x = vy (i)
On differentiating both sides w.r.t y,
dx/dy = v + y(dv/dy)
So,
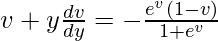
y(dv/dy) = -[ev(1 – v)/(1 + ev)] – v
y(dv/dy) = (-ev + vev – v – vev)/(1 + ev)
y(dv/dy) = -(v + vev)/(1 + ev)
[(1 + ev)/(v + ev)]dv = -(dy/y)
On integrating both sides,
∫[(1 + ev)/(v + ev)]dv = -∫(dy/y)
log|(v + ev)| = -log(y) + log(c)
log|(v + ev)| = log|c/y|
(x/y) + ex/y = c/y
x + yex/y = c (Where ‘c’ is integration constant)
Question 26. (x2 + y2)dy/dx = (8x2 – 3xy + 2y2)
Solution:
We have,
(x2 + y2)dy/dx = (8x2 – 3xy + 2y2)
(dy/dx) = (8x2 – 3xy + 2y2)/(x2 + y2)
It is a homogeneous equation,
So, put y = vx (i)
On differentiating both sides w.r.t x,
dy/dx = v + x(dv/dx)
So,
v + x(dv/dx) = (8x2 – 3xvx + 2v2x2)/(x2 + v2x2)
v + x(dv/dx) = (8 – 3v + 2v2)/(1 + v2)
x(dv/dx) = [(8 – 3v + 2v2)/(1 + v2)] – v
x(dv/dx) = (8 – 4v + 2v2 – v3)/(1 + v2)
(1 + v2)dv/(8 – 4v + 2v2 – v3) = (dx/x)
On integrating both sides,
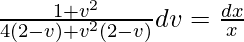
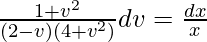
Using partial fraction,
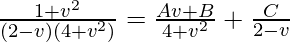
(1 + v2) = Av(2 – v) + B(2 – v) + C(4 + v2)
(1 + v2) = 2Av – Av2 + 2B – Bv + 4C + Cv2
(1 + v2) = (C – A)v2 + (2A – B)v + (2B + 4C)
Comparing the co-efficient of both sides,
(C – A) = 1
(2A – B) = 0
(2B + 4C) = 1
Solving above equations,
A = -(3/8)
B = -(3/4)
C = (5/8)
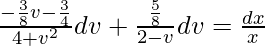
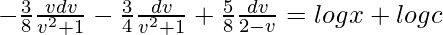
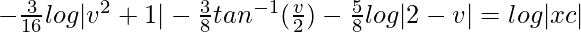
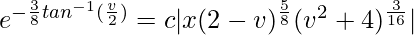
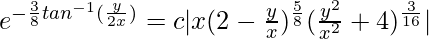
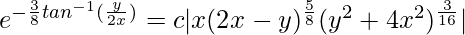 (Where ‘c’ is integration constant)
(Where ‘c’ is integration constant)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...