Class 12 RD Sharma Solutions – Chapter 20 Definite Integrals – Exercise 20.3 | Set 1
Last Updated :
14 Jul, 2021
Evaluate the following integrals:
Question 1(i). 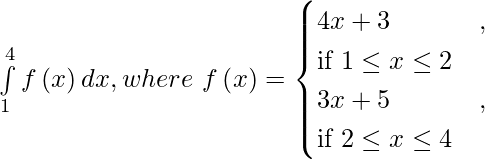
Solution:
We have,
I = 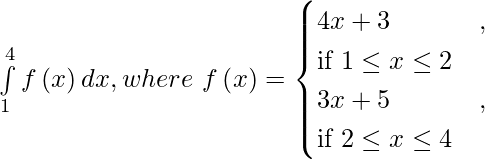
I = 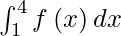
Using additive property, we get
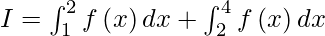
I = 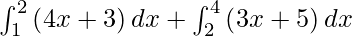
I = ![Rendered by QuickLaTeX.com \left[ 2 x^2 + 3x \right]_1^2 + \left[ \frac{3 x^2}{2} + 5x \right]_2^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cfd2a950c78b02148c91a912a895eecd_l3.png)
I = 8 + 6 – 2 – 3 + 24 + 20 – 6 – 10
I = 37
Question 1(ii). 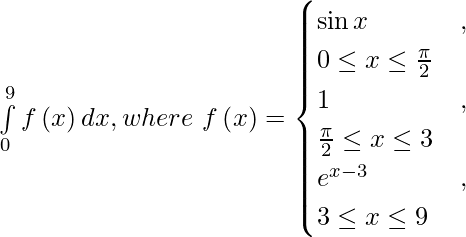
Solution:
We have,
I = 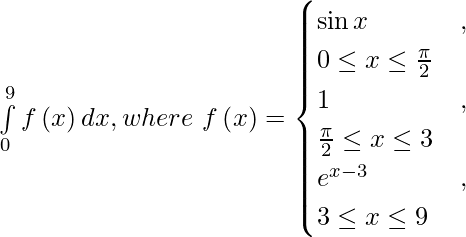
I = 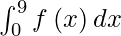
Using additive property, we get
I = 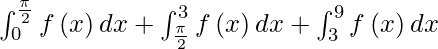
I = 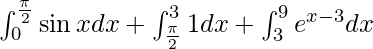
I = ![Rendered by QuickLaTeX.com \left[ - \cos x \right]_0^\frac{\pi}{2} + \left[ x \right]_\frac{\pi}{2}^3 + \left[ e^{x - 3} \right]_3^9](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5171c87c83b53ecfc00b26c61524dd2e_l3.png)
I = 0 + 1 + 3 – π/2 + e6 – e0
I = 3 – π/2 + e6
Question 1(iii). 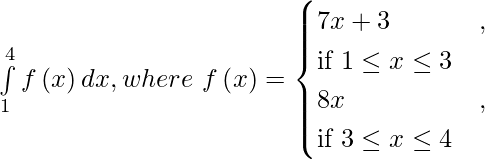
Solution:
We have,
I = 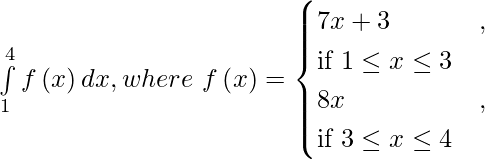
I = 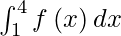
Using additive property, we get
I = 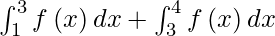
I = 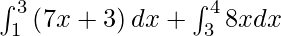
I = ![Rendered by QuickLaTeX.com \left[ \frac{7 x^2}{2} + 3x \right]_1^3 + \left[ 4 x^2 \right]_3^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d63c6468972c11ee76bec87603413b9d_l3.png)
I = 63/2 + 9 – 7/2 – 3 + 64 – 36
I = 56/2 + 34
I = 62
Question 2. 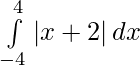
Solution:
We have,
I = 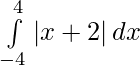
We know that,
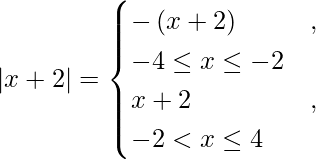
So, we get
I = 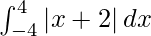
I = 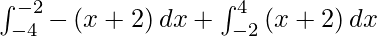
I = ![Rendered by QuickLaTeX.com \left[ - \frac{x^2}{2} - 2x \right]_{- 4}^{- 2} + \left[ \frac{x^2}{2} + 2x \right]_{- 2}^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5f11847804144aa596f317197d1a23b5_l3.png)
I = –2 + 4 – 8 – 8 + 8 + 8 – 2 + 4
I = 20
Question 3. 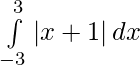
Solution:
We have,
I = 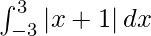
We know that,
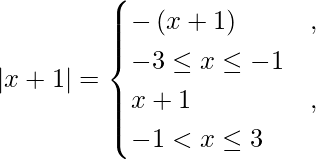
So, we get
I = ![Rendered by QuickLaTeX.com \int_{- 3}^{- 1} - \left( x + 1 \right) d x + \int_{- 1}^3 \left[ x + 1 \right] d x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dbf35b6cc31be3a258b16875335f4831_l3.png)
I = ![Rendered by QuickLaTeX.com \left[ - \frac{\left( x + 1 \right)^2}{2} \right]_{- 3}^{- 1} + \left[ \frac{\left( x + 1 \right)^2}{2} \right]_{- 1}^3](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8c0d527a9da82a789a329ee413155798_l3.png)
I = 0 + 2 + 8 – 0
I = 10
Question 4. 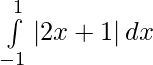
Solution:
We have,
I = 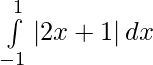
We know that,
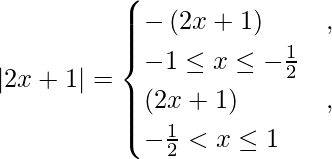
So, we get
I = 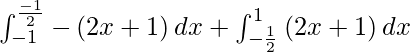
I = ![Rendered by QuickLaTeX.com - \left[ x^2 + x \right]_{- 1}^\frac{- 1}{2} + \left[ x^2 + x \right]_{- \frac{1}{2}}^1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b3cab536497c1c3c08bebc25072618ba_l3.png)
I = –1/4 + 1/2 + 1 – 1 + 1 + 1 – 1/4 + 1/2
I = 5/2
Question 5. 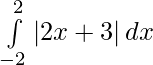
Solution:
We have,
I = 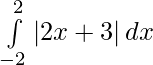
We know that,
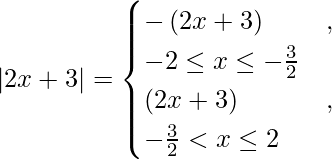
So, we get
I = 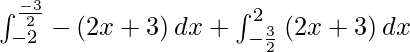
I = ![Rendered by QuickLaTeX.com - \left[ x^2 + 3x \right]_{- 2}^\frac{- 3}{2} + \left[ x^2 + 3x \right]_{- \frac{3}{2}}^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f873b789bb81b89ce921cbabe0973ea6_l3.png)
I = –9/4 + 9/2 + 4 – 6 + 4 + 6 – 9/4 + 9/2
I = 25/2
Question 6. 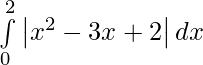
Solution:
We have,
I = 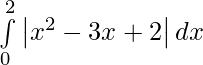
We know that,
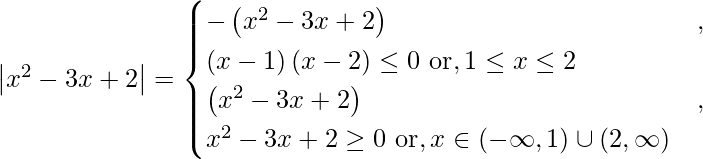
So we get,
I = 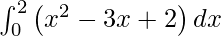
I = 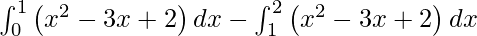
I = ![Rendered by QuickLaTeX.com \left[ \frac{x^3}{3} - \frac{3 x^2}{2} + 2x \right]_0^1 - \left[ \frac{x^3}{3} - \frac{3 x^2}{2} + 2x \right]_1^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9a6b192bbebe69d89530bb089737f673_l3.png)
I = 1/3 – 3/2 + 2 – [8/3 – 6 + 4 – 1/3 + 3/2 – 2]
I = 1/3 – 3/2 + 2 – 8/3 + 6 – 2 + 1/3 – 3/2
I = 1
Question 7. 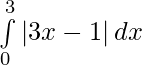
Solution:
We have,
I = 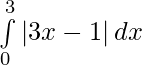
We know that,
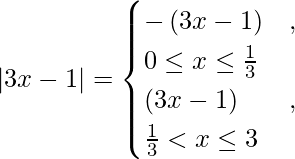
So we get,
I = 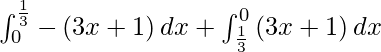
I = ![Rendered by QuickLaTeX.com \left[ \frac{- 3 x^2}{2} - x \right]_0^\frac{1}{3} + \left[ \frac{3 x^2}{2} + x \right]_\frac{1}{3}^3](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a00aaa16816f4aab1c5fdc18321c57da_l3.png)
I = –1/6 + 1/3 – 0 + 27/2 + 3 – 1/6 – 1/3
I = 65/6
Question 8. 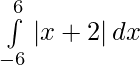
Solution:
We have,
I = 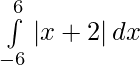
We know that,
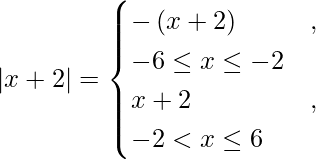
So, we get
I = 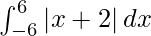
I = 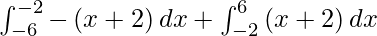
I = ![Rendered by QuickLaTeX.com \left[ \frac{- x^2}{2} - 2x \right]_{- 6}^{- 2} + \left[ \frac{x^2}{2} + 2x \right]_{- 2}^6](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-873f9b23a60857a11ee257ba7ea3949b_l3.png)
I = –2 + 4 + 18 – 12 + 18 + 12 – 2 + 4
I = 40
Question 9. 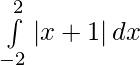
Solution:
We have,
I = 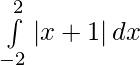
We know that,
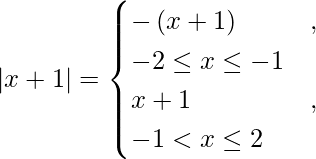
So we get,
I = 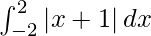
I = 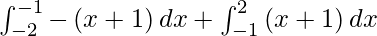
I = ![Rendered by QuickLaTeX.com \left[ \frac{- x^2}{2} - x \right]_{- 2}^{- 1} + \left[ \frac{x^2}{2} + x \right]_{- 1}^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-12e039cf05c2fd8bc0a96092c793c263_l3.png)
I = -1/2 + 1 + 2 – 2 + 2 + 2 – 1/2 + 1
I = 5
Question 10. 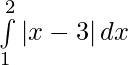
Solution:
We have,
I = 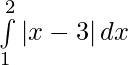
We know that,
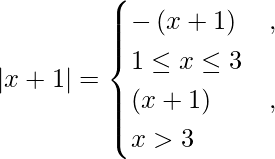
So we get,
I = 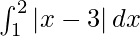
I = 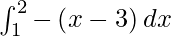
I = ![Rendered by QuickLaTeX.com \left[ \frac{- x^2}{2} - 3x \right]_1^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f95e78b00a2020ca31bef47886550159_l3.png)
I = – 2 – 6 + 1/2 + 3
I = – 5 + 1/2
I = (-10 + 1)/2
I = -9/2
Question 11. 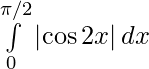
Solution:
We have,
I = 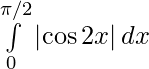
We know that,
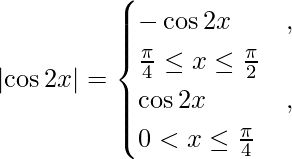
So we get,
I = 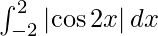
I = 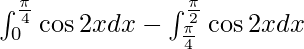
I = ![Rendered by QuickLaTeX.com \left[ \frac{\sin 2x}{2} \right]_0^\frac{\pi}{4} - \left[ \frac{\sin 2x}{2} \right]_\frac{\pi}{4}^\frac{\pi}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-33167585a32622bd996792b1db8cf20c_l3.png)
I = 1/2 – 0 – 0 + 1/2
I = 1
Question 12. 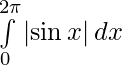
Solution:
We have,
I = 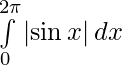
We know that,
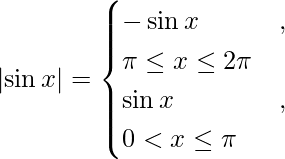
So we get,
I = 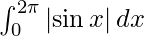
I = 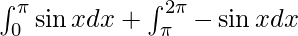
I = ![Rendered by QuickLaTeX.com - \left[ \cos x \right]_0^\pi + \left[ \cos x \right]_\pi^{2\pi}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-88a8fae15a1573bb7c8d326cc7c4ea18_l3.png)
I = 1 + 1 + 1 – (–1)
I = 1 + 1 + 1 + 1
I = 4
Question 13. 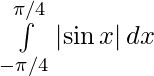
Solution:
We have,
I = 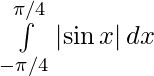
We know that,
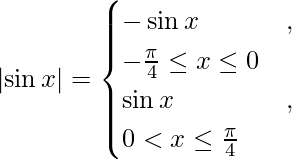
So we get,
I = 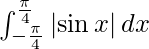
I = 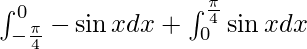
I = ![Rendered by QuickLaTeX.com \left[ \cos x \right]_\frac{- \pi}{4}^0 - \left[ \cos x \right]_0^\frac{- \pi}{4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2839acf2dac96af92939c79bde41e90a_l3.png)
I = 1 – 1/√2 – 1/√2 + 1
I = 2 – 2/√2
I = 2 – √2
Question 14. 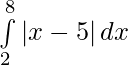
Solution:
We have,
I = 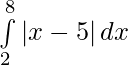
We know that,
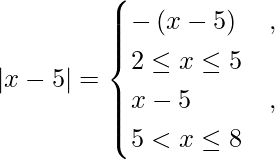
So we get,
I = 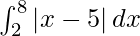
I = 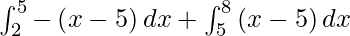
I = ![Rendered by QuickLaTeX.com - \left[ \frac{x^2}{2} - 5x \right]_2^5 + \left[ \frac{x^2}{2} - 5x \right]_5^8](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b34aa33ee66678b5aec48cba2d0d343b_l3.png)
I = – 25/2 + 25 + 2 – 10 + 32 – 40 – 25/2 + 25
I = 9
Share your thoughts in the comments
Please Login to comment...