Class 12 RD Sharma Solutions – Chapter 20 Definite Integrals – Exercise 20.5 | Set 1
Last Updated :
20 May, 2021
Evaluate the following definite integrals as limits of sums:
Question 1. 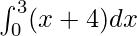
Solution:
We have,
I =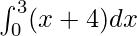
We know,![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec1277fbc436270e411e9500bd03e5d8_l3.png) , where h =
, where h =
Here a = 0, b = 3 and f(x) = x + 4.
=> h = 3/n
=> nh = 3
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4+(h+4)+(2h+4)+...+(n-1)h+4]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6adec80c51ba172c5bb4c618f2a96321_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4n+h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-772638737d568446acd982bec039c696_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[4n+h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-30bdb5367aed4a95421c5edfb5655c9e_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{3}{n}[4n+\frac{3}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7e54bed4ac3be33a7c753d66307cc0d7_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\left[12+\frac{9}{2}(1-\frac{1}{n})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7e0deb8bc99434ddd4eaa539a19a6019_l3.png)
= 12 + 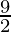
=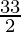
Therefore, the value of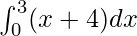 as limit of sum is
as limit of sum is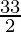 .
.
Question 2. 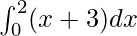
Solution:
We have,
I =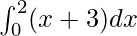
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec1277fbc436270e411e9500bd03e5d8_l3.png) , where h =
, where h =
Here a = 0, b = 2 and f(x) = x + 3.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[3+(h+3)+(2h+3)+...+(n-1)h+3]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4af6bff67cbb9ed688229bdfa080e71a_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[3n+h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-37d78bf49a095daaecf69c5542788d9e_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[3n+h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-66b19c94f4c3ec6524f3acfd4f920a22_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[3n+\frac{2}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-951b6ceeb83e619be25eb6bf93d3c979_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[6+2(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-655a6b266d84cd98c3655198d9c6656d_l3.png)
= 6 + 2
= 8
Therefore, the value of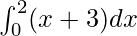 as limit of sum is 8.
as limit of sum is 8.
Question 3. 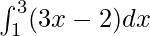
Solution:
We have,
I =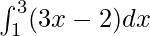
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec1277fbc436270e411e9500bd03e5d8_l3.png) , where h =
, where h =
Here a = 1, b = 3 and f(x) = 3x − 2.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ff4359373787dc7ac96481b49136a0c_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[1+[3(1+h)-2]+[3(1+2h)-2]+...+[3(1+(n-1)h)-2]]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-06a140f3e882495d63adf08b0d8fc842_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[n+3h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b7a63a086c3d7904b7ee9b33e31f365b_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[n+3h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-da3d6faf78acbd517e360efb5e0b13b4_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[n+\frac{6}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a8475dd7ee1c6c54eb67bc6d66c12a91_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[2+6(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1325b9b0b233c8ce714126b7910de6fd_l3.png)
= 2 + 6
= 8
Therefore, the value of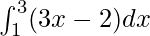 as limit of sum is 8.
as limit of sum is 8.
Question 4. 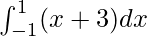
Solution:
We have,
I =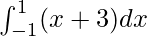
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec1277fbc436270e411e9500bd03e5d8_l3.png) , where h =
, where h =
Here a = −1, b = 1 and f(x) = x + 3.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(-1)+f(-1+h)+f(-1+2h)+...+f(-1+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ea28c7c96d466dc9769dc6e207a0d976_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[2+(2+h)+(2+2h)+...+((n-1)h+2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d6cac2268f64b951a4c31cf4b08ee7be_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[2n+h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c7d83bb96991e61d5943e2eaaf9bb1da_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[2n+h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-719bdff1e8b6b85899b7cd6fb9b2a368_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[2n+\frac{2}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-56e5a953b7abee565baa8ea3668fcb43_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[4+2(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-71e5349a8aa0ee70b133e06290aa8676_l3.png)
= 4 + 2
= 6
Therefore, the value of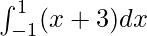 as limit of sum is 6.
as limit of sum is 6.
Question 5. 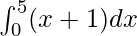
Solution:
We have,
I =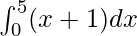
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec1277fbc436270e411e9500bd03e5d8_l3.png) , where h =
, where h =
Here a = 0, b = 5 and f(x) = x + 1.
=> h = 5/n
=> nh = 5
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[1+(h+1)+(2h+1)+...+((n-1)h+1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a50a569f42b8f59dc7e36850a196d0d_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[n+h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ecfe821660fb52955685ce0b20947197_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[n+h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-46b0de65731191d37a398f3e3be4a384_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{5}{n}[n+\frac{5}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-17869b8c206d6bde178845223140547e_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[5+\frac{25}{2}(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8bfba295f8aa9009daf029b610130970_l3.png)
= 5 +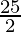
=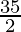
Therefore, the value of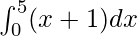 as limit of sum is
as limit of sum is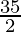 .
.
Question 6. 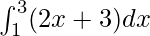
Solution:
We have,
I =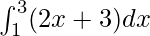
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec1277fbc436270e411e9500bd03e5d8_l3.png) , where
, where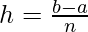
Here a = 1, b = 3 and f(x) = 2x + 3.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ff4359373787dc7ac96481b49136a0c_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[2+3+[2(1+h)+3]+[2(1+2h)+3]+...+[2(1+(n-1)h+3)]]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2f92c117052d65095d2a677da603bc6a_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[5+(5+2h)+(5+4h)+...+(5+2(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-893ed764e23486b93f8a1d1e23317649_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[5n+2h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ae19fe88526297d885480b777161cb2e_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[5n+2h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9179fc7cfa82bac471f9777d03e72761_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[5n+\frac{4}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0bcf7ef07371c15941bb5b7764ec1a87_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[10+4(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a0de9d4ebf4a5b6c9872f396fc99f69b_l3.png)
= 10 + 4
= 14
Therefore, the value of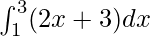 as limit of sum is 14.
as limit of sum is 14.
Question 7. 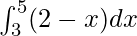
Solution:
We have,
I =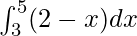
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec1277fbc436270e411e9500bd03e5d8_l3.png) , where h =
, where h =
Here a = 3, b = 5 and f(x) = 2 − x.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(3)+f(3+h)+f(3+2h)+...+f(3+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-35fa7a19a3c2d8266dbd18e6d75d9a39_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[(2-3)+(2-(3+h))+f(2-(3+2h))+...+f(2-(3+(n-1)h))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-43dafc426c7e8b2719c1f247ca218804_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[-1+(-1-h)+(-1-2h)+...+(-1-(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c63862f3337c96e8f280223d261a9350_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[-n-h(1+2+3+...+(n-1))]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fa7c3dcfb34b191b2a5a87641b27e024_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[-n-h(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cdbd9caa70a316c47654080c0d071fbb_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[-n-\frac{2}{n}(\frac{n(n-1)}{2})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1f1e9dfc10c857ddf2235116a6b8cdb0_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[-2-2(1-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3c5e8227ab9c519e221e5121787a1588_l3.png)
= –2 – 2
= –4
Therefore, the value of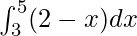 as limit of sum is –4.
as limit of sum is –4.
Question 8. 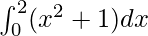
Solution:
We have,
I =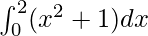
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec1277fbc436270e411e9500bd03e5d8_l3.png) , where h =
, where h =
Here a = 0, b = 2 and f(x) = x2 + 1.
=> h = 2/n
=> nh = 2
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(0)+f(h)+f(2h)+...+f((n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00f39d67ae55d552f96ec5ac823cd814_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[1+(h^2+1)+((2h)^2+1)+...+(((n-1)h)^2+1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5fccf88a240b394e20e738a20c2c6689_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[n+h^2(1^2+2^2+3^2+...+(n-1)^2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9a0c946e4a6c296f45f9a1b42a0c4bb7_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[n+h^2\frac{n(n-1)(2n-1)}{6}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-487cae23ff0dfea2b721af45cbb14cb6_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{2}{n}[n+\frac{4}{n^2}\frac{n(n-1)(2n-1)}{6}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aa732330834ff3bec2431bdc28bc17d4_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[2+\frac{4n^3}{3n^3}(1-\frac{1}{n})(2-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5d60083eaf75a7024cdce3cc0741aafa_l3.png)
=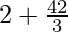
=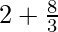
=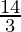
Therefore, the value of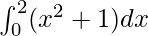 as limit of sum is
as limit of sum is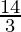 .
.
Question 9. 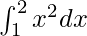
Solution:
We have,
I =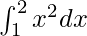
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec1277fbc436270e411e9500bd03e5d8_l3.png) , where h =
, where h =
Here a = 1, b = 2 and f(x) = x2.
=> h = 1/n
=> nh = 1
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ff4359373787dc7ac96481b49136a0c_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[1+(1+h)^2+(1+2h)^2+...+(1+(n-1)h)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3aa1717f65b249851442aec74cebfb91_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[1+(1+2h+h^2)+(1+4h+4h^2)+...+(1+2(n-1)h+(n-1)^2h^2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-28cb41ba30a1992f894c89ee89ad648d_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[n+2h(1+2+3+...+(n-1))+h^2(1^2+2^2+3^2+...+(n-1)^2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-28e0eb39e5466e08dc381e9b3e97cce6_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[n+2h(\frac{n(n-1)}{2})+h^2(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54abc7776e148c7ace03148adb382dcb_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{1}{n}[n+\frac{2}{n}(\frac{n(n-1)}{2})+\frac{1}{n^2}(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6b0f016472165210e3a3536531bc7099_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[1+(1-\frac{1}{n})+\frac{n^3}{6n^3}(1-\frac{1}{n})(2-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0dedf2910571c7e9e940e3294cd4d986_l3.png)
= 1 + 1 +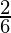
= 1 + 1 +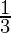
=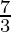
Therefore, the value of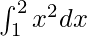 as limit of sum is
as limit of sum is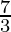 .
.
Question 10. 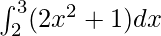
Solution:
We have,
I =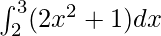
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec1277fbc436270e411e9500bd03e5d8_l3.png) , where h =
, where h =
Here a = 2, b = 3 and f(x) = 2x2 + 1.
=> h = 1/n
=> nh = 1
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(2)+f(2+h)+f(2+2h)+...+f(2+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc18938dd8a01b1c881a44f0feefe6cd_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[9+[2(2+h)^2+1]+[2(2+2h)^2+1]+...+[2(2+(n-1)h)^2+1]]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b1f8e65c132fd23775fcd1b7cd55b440_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[9n+8h(1+2+3+...+(n-1))+2h^2(1^2+2^2+3^2+...(n-1)^2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d38389c6fbaa0cafe0d4ca103d209b41_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[9n+8h(\frac{n(n-1)}{2})+2h^2(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1d82314d2eedbb46ca48508c8fb71c55_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{1}{n}[9n+\frac{8}{n}(\frac{n(n-1)}{2})+\frac{2}{n^2}(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cd6ba200dd3c58a21a2e269e24fea85a_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[9+\frac{4n^2}{n^2}(1-\frac{1}{n})+\frac{n^3}{3n^3}(1-\frac{1}{n})(2-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-28db4d1b10d50beceeaf16477b15b68c_l3.png)
= 9 + 4 +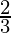
=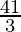
Therefore, the value of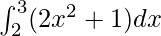 as limit of sum is
as limit of sum is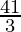 .
.
Question 11. 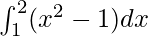
Solution:
We have,
I =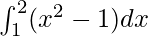
We know,
![Rendered by QuickLaTeX.com \int_{a}^{b}f(x)dx=\lim_{h\to0}h[f(a)+f(a+h)+f(a+2h)+...+f(a+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec1277fbc436270e411e9500bd03e5d8_l3.png) , where h =
, where h =
Here a = 1, b = 2 and f(x) = x2 − 1.
=> h = 1/n
=> nh = 1
So, we get,
I =![Rendered by QuickLaTeX.com \lim_{h\to0}h[f(1)+f(1+h)+f(1+2h)+...+f(1+(n-1)h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ff4359373787dc7ac96481b49136a0c_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[(1^2-1)+[(1+h)^2-1]+[(1+2h)^2-1]+...+[(1+(n-1)h)^2-1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7f5b4b1cc25112b806f9c386324f2675_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[0+2h(1+2+3+...+(n-1))+h^2(1^2+2^2+3^2+...+(n-1)^2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-23c2099b5feb5990d45663e37ad038ae_l3.png)
=![Rendered by QuickLaTeX.com \lim_{h\to0}h[2h(\frac{n(n-1)}{2})+h^2(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-117cab4ad253cc1007addb6beb6cb5a6_l3.png)
Now if h −> 0, then n −> ∞. So, we have,
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}\frac{1}{n}[\frac{2}{n}(\frac{n(n-1)}{2})+\frac{1}{n^2}(\frac{n(n-1)(2n-1)}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b3cff4913b1a2336d1948b7bed0ceee6_l3.png)
=![Rendered by QuickLaTeX.com \lim_{n\to\infty}[\frac{n^2}{n^2}(1-\frac{1}{n})+\frac{n^3}{6n^3}(1-\frac{1}{n})(2-\frac{1}{n})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ce3d1eee0fb156edfe92dcdfd5b57c43_l3.png)
= 1 +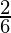
= 1 +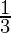
=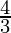
Therefore, the value of 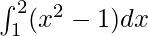 as limit of sum is
as limit of sum is 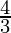 .
.
Share your thoughts in the comments
Please Login to comment...