Evaluate the following definite integrals:
Question 21. 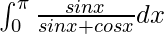
Solution:
We have,
I = 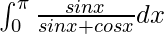
Let sin x = A (sin x + cos x) + B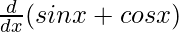
=> sin x = A (sin x + cos x) + B (cos x – sin x)
=> sin x = sin x (A – B) + cos x (A + B)
On comparing both sides, we get
A – B = 1 and A + B = 0
On solving, we get A = 1/2 and B = –1/2.
Therefore, the expression becomes,
I = 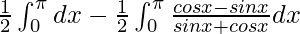
I = ![Rendered by QuickLaTeX.com \left[\frac{x}{2}\right]_0^\pi-\frac{1}{2}\left[\log(sinx+cosx)\right]_{0}^{\pi}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d945ce735ba7d0a2b863d1cbc9aabfc1_l3.png)
I = 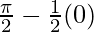
I = 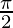
Therefore, the value of 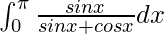 is
is 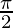 .
.
Question 22. 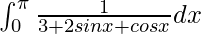
Solution:
We have,
I = 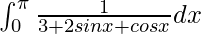
On putting cos x = 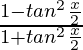 and sin x =
and sin x = 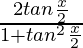 , we get,
, we get,
I = 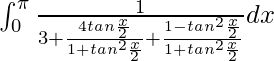
I = 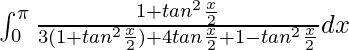
I = 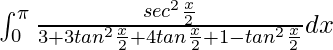
I = 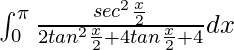
Let tan x/2 = t. So, we have
=> 1/2 sec2 x/2 dx = dt
=> sec2 x/2 dx = 2 dt
Now, the lower limit is, x = 0
=> t = tan x/2
=> t = tan 0/2
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π
=> t = tan x/2
=> t = tan π/2
=> t = ∞
So, the equation becomes,
I = 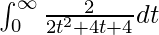
I = 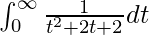
I = 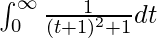
I = ![Rendered by QuickLaTeX.com \left[tan^{-1}(t+1)\right]^\infty_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-10849ac63bd4d7e0df1665b3efb7cdc8_l3.png)
I = 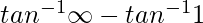
I = 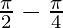
I = 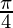
Therefore, the value of 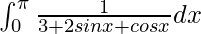 is
is 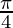 .
.
Question 23. 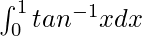
Solution:
We have,
I = 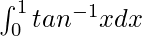
I = 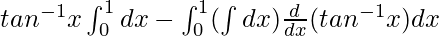
I = ![Rendered by QuickLaTeX.com \left[xtan^{-1}x\right]_{0}^{1}-\int_{0}^1\frac{x}{1+x^2}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cce01913baeccd3fa49b6e8d996b18bc_l3.png)
I = ![Rendered by QuickLaTeX.com \left[xtan^{-1}x\right]_{0}^{1}-\frac{1}{2}\int_{0}^1\frac{2x}{1+x^2}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7844c42e84678813ac1c25c8600b45a9_l3.png)
I = ![Rendered by QuickLaTeX.com \left[xtan^{-1}x\right]_{0}^{1}-\frac{1}{2}\left[log(1+x^2)\right]_{0}^1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6c57d5190e51a678aee79fffcf9b88fd_l3.png)
I = ![Rendered by QuickLaTeX.com (\frac{\pi}{4}-0)-\frac{1}{2}\left[log(1+1)-log(1+0)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a0d46ea86dbde99d42752905f963f450_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{\pi}{4}-\frac{1}{2}\left[log2-log1\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6c388c93444ff4f3579944819a01a8eb_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{\pi}{4}-\frac{1}{2}\left[log2-0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-699ff9945f7bf8205068ef566f62b804_l3.png)
I = 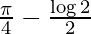
Therefore, the value of 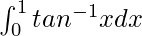 is
is 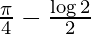 .
.
Question 24. 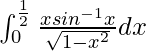
Solution:
We have,
I = 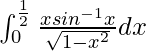
Let sin–1 x = t. So, we have
=> 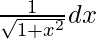 = dt
= dt
Now, the lower limit is, x = 0
=> t = sin–1 x
=> t = sin–1 0
=> t = 0
Also, the upper limit is, x = 1/2
=> t = sin–1 x
=> t = sin–1 1/2
=> t = π/6
So, the equation becomes,
I = 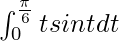
I = 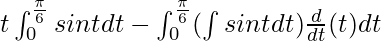
I = ![Rendered by QuickLaTeX.com \left[-tcost\right]_{0}^{\frac{\pi}{6}}+\int_{0}^{\frac{\pi}{6}}costdt](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6a9c170568bd070c4e5f74f0447c0139_l3.png)
I = ![Rendered by QuickLaTeX.com \left[-tcost\right]_{0}^{\frac{\pi}{6}}+\left[sint\right]_{0}^{\frac{\pi}{6}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4b30f0d352a4d51fa63b1f5792b84a69_l3.png)
I = ![Rendered by QuickLaTeX.com \left[-\frac{\pi}{6}(\frac{\sqrt{3}}{2})+0\right]+\left[sin\frac{\pi}{6}-0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8cee6e703df4af0f27bd94c4fa37644c_l3.png)
I = 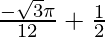
I = 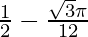
Therefore, the value of 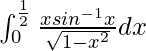 is
is 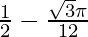 .
.
Question 25. 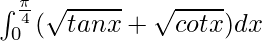
Solution:
We have,
I = 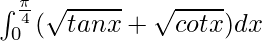
I = 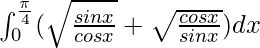
I = 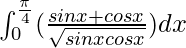
I = 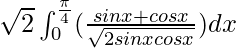
I = 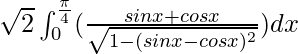
Let sinx – cosx = t. So, we have
=> (cos x + sin x) dx = dt
Now, the lower limit is, x = 0
=> t = sinx – cosx
=> t = sin 0 – cos 0
=> t = 0 – 1
=> t = –1
Also, the upper limit is, x = π/4
=> t = sinx – cosx
=> t = sin π/4 – cos π/4
=> t = sin π/4 – sin π/4
=> t = 0
So, the equation becomes,
I = 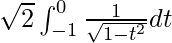
I = ![Rendered by QuickLaTeX.com \sqrt{2}\left[sin^{-1}t\right]_{-1}^{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0c229d24b015cd9fc9e69f9365c07ff_l3.png)
I = ![Rendered by QuickLaTeX.com \sqrt{2}\left[sin^{-1}0-sin^{-1}(-1)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-637b45c9d0c9646a48dada34c439733a_l3.png)
I = ![Rendered by QuickLaTeX.com \sqrt{2}\left[0+sin^{-1}(1)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-10fe935bb64d21c0df2527c901a64600_l3.png)
I = 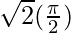
I = 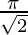
Therefore, the value of 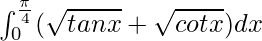 is
is 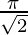 .
.
Question 26. 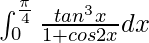
Solution:
We have,
I = 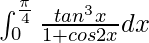
I = 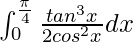
I = 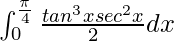
I = 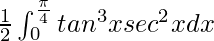
Let tan x = t. So, we have
=> sec2 x dx = dt
Now, the lower limit is, x = 0
=> t = tan x
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π/4
=> t = tan x
=> t = tan π/4
=> t = 1
So, the equation becomes,
I = 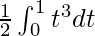
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{t^4}{4}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5b523dd76a0034a3c23d8ffe48b7fe74_l3.png)
I = 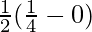
I = 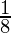
Therefore, the value of 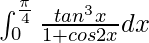 is
is 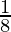 .
.
Question 27. 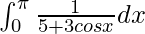
Solution:
We have,
I = 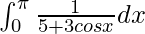
On putting cos x = 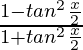 , we get
, we get
I = 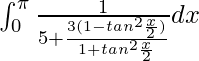
I = 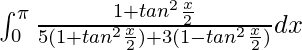
I = 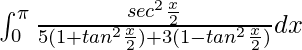
Let tan x/2 = t. So, we have
=> 1/2 sec2 x/2 dx = dt
=> sec2 x/2 dx = 2 dt
Now, the lower limit is, x = 0
=> t = tan x/2
=> t = tan 0/2
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π
=> t = tan x/2
=> t = tan π/2
=> t = ∞
So, the equation becomes,
I = 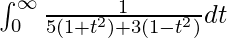
I = 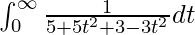
I = 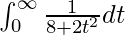
I = 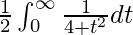
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[tan^{-1}\frac{t}{2}\right]_{0}^{\infty}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-49456556b7e02a38d7f40aa3b072a080_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[tan^{-1}\frac{\infty}{2}-\tan^{-1}\frac{0}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d6d732419380fbbcb7f3a5466e481205_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[tan^{-1}\infty-\tan^{-1}0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dc2172747fd6f30962b18beb38375300_l3.png)
I = 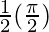
I = 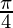
Therefore, the value of 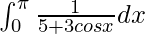 is
is 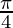 .
.
Question 28. 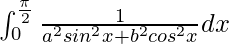
Solution:
We have,
I = 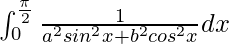
I = 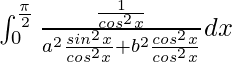
I = 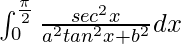
I = 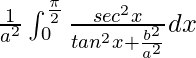
Let tan x = t. So, we have
=> sec2 x dx = dt
Now, the lower limit is, x = 0
=> t = tan x
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π/2
=> t = tan x
=> t = tan π/2
=> t = ∞
So, the equation becomes,
I = 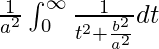
I = ![Rendered by QuickLaTeX.com \frac{1}{a^2}\left[\frac{a}{b}tan^{-1}\frac{at}{b}\right]_{0}^{\infty}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9e82532da479056ed6964249241a8456_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{a^2}\left[\frac{a}{b}tan^{-1}\infty-\frac{a}{b}tan^{-1}0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-61bd5cef6afd00e9e887fa9170cc3ca2_l3.png)
I = 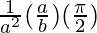
I = 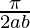
Therefore, the value of 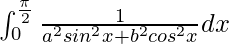 is
is 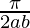 .
.
Question 29. 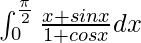
Solution:
We have,
I = 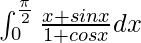
I = 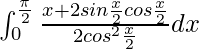
I = 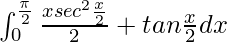
I = ![Rendered by QuickLaTeX.com \left[xtan\frac{x}{2}-\int_{0}^{\frac{\pi}{2}}tan\frac{x}{2}dx+\int_{0}^{\frac{\pi}{2}}tan\frac{x}{2}dx\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-52ea5a5994f4fae1034cc5e8a661812e_l3.png)
I = ![Rendered by QuickLaTeX.com \left[xtan\frac{x}{2}\right]^\frac{\pi}{2}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cadff092bb75e00a822a8c1bf7fd7e08_l3.png)
I = 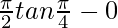
I = 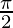
Therefore, the value of 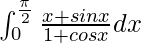 is
is 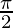 .
.
Question 30. 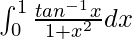
Solution:
We have,
I = 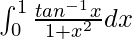
Let tan–1 x = t. So, we have
=> 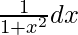 = dt
= dt
Now, the lower limit is, x = 0
=> t = tan–1 x
=> t = tan–1 0
=> t = 0
Also, the upper limit is, x = 1
=> t = tan–1 x
=> t = tan–1 1
=> t = π/4
So, the equation becomes,
I = 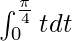
I = ![Rendered by QuickLaTeX.com \left[\frac{t^2}{2}\right]_{0}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-41bf1dbb85d90b4ddf9fdae996e95d2a_l3.png)
I = 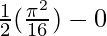
I = 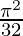
Therefore, the value of 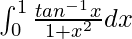 is
is 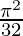 .
.
Question 31. 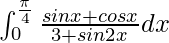
Solution:
We have,
I = 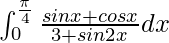
I = 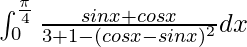
I = 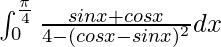
I = ![Rendered by QuickLaTeX.com \left[\frac{1}{4}log|\frac{2+sinx-cosx}{2-sinx+cosx}|\right]_{0}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3c9c9f5744510793d62e3fd90e340cac_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{4}\left[log|\frac{2+sin\frac{\pi}{4}-cos\frac{\pi}{4}}{2-sin\frac{\pi}{4}+cos\frac{\pi}{4}}|-log\frac{2+0-1}{2-0+1}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cd42391eb3a8d30330f11d89d5a5acdc_l3.png)
I = 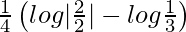
I = 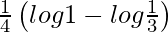
I = 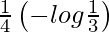
I = 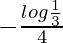
I = 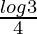
Therefore, the value of 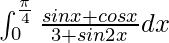 is
is 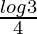 .
.
Question 32. 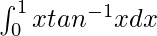
Solution:
We have,
I = 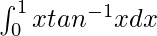
On using integration by parts, we get
I = 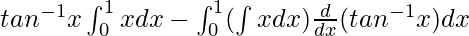
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1\frac{x^2}{1+x^2}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e5ad5a884573bcca405da5b00e643d45_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1\frac{1+x^2-1}{1+x^2}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e379ad59b4504a54e8d2994b223e3b4a_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1\frac{1+x^2}{1+x^2}dx+\frac{1}{2}\int_0^1\frac{1}{1+x^2}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25504336990fd491983660f8d864f44f_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1\frac{1+x^2}{1+x^2}dx+\frac{1}{2}\int_0^1\frac{1}{1+x^2}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25504336990fd491983660f8d864f44f_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\int_0^1dx+\frac{1}{2}\int_0^1\frac{1}{1+x^2}dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0318f3bd2c10a15a84b10009b2913d7a_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{x^2tan^{-1}x}{2}\right]_{0}^{1}-\frac{1}{2}\left[x\right]_0^1+\frac{1}{2}\left[tan^{-1}x\right]_0^1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-efbac77c0432844db5e99575d1c237f6_l3.png)
I = ![Rendered by QuickLaTeX.com (\frac{\pi}{8}-0)-\frac{1}{2}(1-0)+\frac{1}{2}\left[tan^{-1}1-tan^{-1}0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ebff9767666558f217dc7d13a98918d0_l3.png)
I = 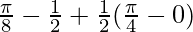
I = 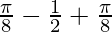
I = 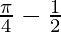
Therefore, the value of 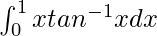 is
is 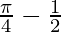 .
.
Question 33. 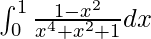
Solution:
We have,
I = 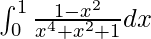
I = 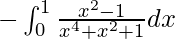
I = 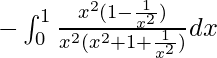
I = 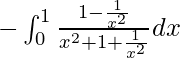
I = 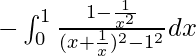
I = ![Rendered by QuickLaTeX.com -\left[\frac{1}{2}\log|\frac{x+\frac{1}{x}-1}{x+\frac{1}{x}+1}|\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f0cda8830c7239b929cdb2623b397f8c_l3.png)
I = ![Rendered by QuickLaTeX.com -\left[\frac{1}{2}\log|\frac{x^2-x+1}{x^2+x+1}|\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cdbe08c26b7db53d961c079487b5043c_l3.png)
I = 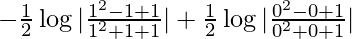
I = 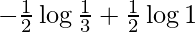
I = 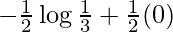
I = 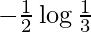
I = 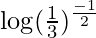
I = 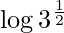
I = 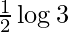
Therefore, the value of 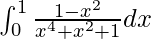 is
is 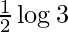 .
.
Question 34. 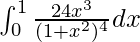
Solution:
We have,
I = 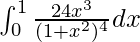
Let 1 + x2 = t. So, we have
=> 2x dx = dt
Now, the lower limit is, x = 0
=> t = 1 + x2
=> t = 1 + 02
=> t = 1 + 0
=> t = 1
Also, the upper limit is, x = π
=> t = 1 + x2
=> t = 1 + 12
=> t = 1 + 1
=> t = 2
So, the equation becomes,
I = 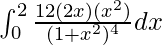
I = 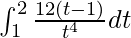
I = 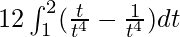
I = 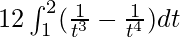
I = ![Rendered by QuickLaTeX.com 12\left[\frac{-1}{2t^2}-\frac{1}{3t^3}\right]_{1}^{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e8dc0520881da08439b8620491980e47_l3.png)
I = ![Rendered by QuickLaTeX.com 12\left[\frac{-1}{8}+\frac{1}{24}+\frac{1}{2}-\frac{1}{3}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-135a500ac710d4bcc8c93d095310bbd0_l3.png)
I = ![Rendered by QuickLaTeX.com 12\left[\frac{-3+1+12-8}{24}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-32e7ff1664af618cf6fb1515ddfda559_l3.png)
I = 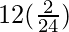
I = 1
Therefore, the value of 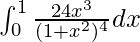 is 1.
is 1.
Question 35. 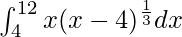
Solution:
We have,
I = 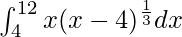
Let x – 4 = t3. So, we have
=> dx = 3t2 dt
Now, the lower limit is, x = 4
=> t3 = x – 4
=> t3 = 4 – 4
=> t3 = 0
=> t = 0
Also, the upper limit is, x = 12
=> t3 = x – 4
=> t3 = 12 – 4
=> t3 = 8
=> t = 2
So, the equation becomes,
I = 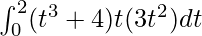
I = 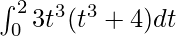
I = 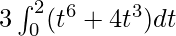
I = ![Rendered by QuickLaTeX.com 3\left[\frac{t^7}{7}+t^4\right]_{0}^{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c16512d9ae43744d2391601256185c5f_l3.png)
I = ![Rendered by QuickLaTeX.com 3\left[\frac{128}{7}+16-0-0\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d211904dd1f07c3844cf8f49ce10cd70_l3.png)
I = 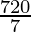
Therefore, the value of 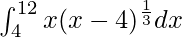 is
is 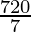 .
.
Question 36. 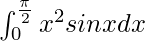
Solution:
We have,
I = 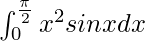
On using integration by parts, we get
I = 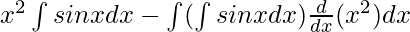
I = 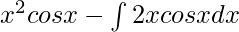
I = ![Rendered by QuickLaTeX.com x^2cosx+2[x\int cosxdx-\int(\int cosxdx)\frac{dx}{dx}dx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4574de68abe1306023f903924ab6a593_l3.png)
I = ![Rendered by QuickLaTeX.com x^2cosx+2[xsinxdx-\int sinxdx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d66176186e7297210b158433efcfab77_l3.png)
I = ![Rendered by QuickLaTeX.com \left[x^2cosx+2xsinxdx+2cosx\right]_0^{\frac{\pi}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-206613bf558fc44810456813a39ca532_l3.png)
I = π + 0 – 0 – 0 – 2
I = π – 2
Therefore, the value of 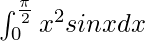 is π – 2.
is π – 2.
Question 37. 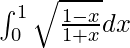
Solution:
We have,
I = 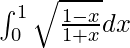
Let x = cos 2t. So, we have
=> dx = – 2 sin 2t dt
Now, the lower limit is, x = 0
=> cos 2t = x
=> cos 2t = 0
=> 2t = π/2
=> t = π/4
Also, the upper limit is, x = 1
=> cos 2t = x
=> cos 2t = 1
=> 2t = 0
=> t = 0
So, the equation becomes,
I = 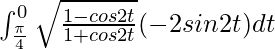
I = 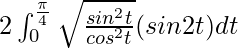
I = 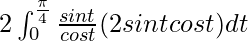
I = 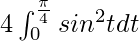
I = 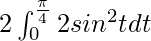
I = 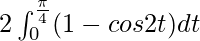
I = ![Rendered by QuickLaTeX.com 2\left[t-\frac{sin^2t}{2}\right]^{\frac{\pi}{4}}_{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dd6aa1bbbaba469a20fb7604a33e5e66_l3.png)
I = ![Rendered by QuickLaTeX.com 2\left[\frac{\pi}{4}-\frac{1}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5277bf3dd342e2e4e890f5cb7c8ed5d6_l3.png)
I = 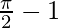
Therefore, the value of 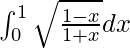 is
is 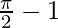 .
.
Question 38. 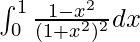
Solution:
We have,
I = 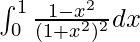
I = 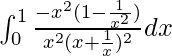
I = 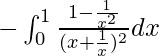
Let x + 1/x = t. So, we have
=> (1 – 1/x2)dx = dt
Now, the lower limit is, x = 0
=> t = x + 1/x
=> t = ∞
Also, the upper limit is, x = 1
=> t = x + 1/x
=> t = 1 + 1
=> t = 2
So, the equation becomes,
I = 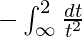
I = 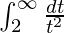
I = ![Rendered by QuickLaTeX.com \left[\frac{-1}{t}\right]^{\infty}_{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ddce542b40d6efa9b06e3d506b6f0a40_l3.png)
I = 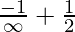
I = 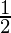
Therefore, the value of 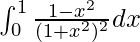 is
is  .
.
Question 39. 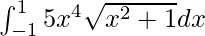
Solution:
We have,
I = 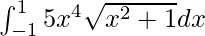
Let x5 + 1 = t. So, we have
=> 5x4 dx = dt
Now, the lower limit is, x = –1
=> t = x5 + 1
=> t = (–1)5 + 1
=> t = –1 + 1
=> t = 0
Also, the upper limit is, x = 1
=> t = x5 + 1
=> t = (1)5 + 1
=> t = 1 + 1
=> t = 2
So, the equation becomes,
I = 
I = ![Rendered by QuickLaTeX.com \left[\frac{2}{3}t^{\frac{3}{2}}\right]_{0}^{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-956089bf0bd15b42d1600f47ffb12c58_l3.png)
I = 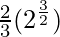
I = 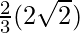
I = 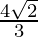
Therefore, the value of 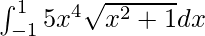 is
is 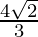 .
.
Question 40. 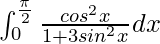
Solution:
We have,
I = 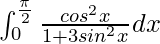
I = 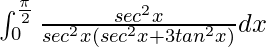
Let tan x = t. So, we have
=> sec2 x dx = dt
Now, the lower limit is, x = 0
=> t = tan x
=> t = tan 0
=> t = 0
Also, the upper limit is, x = π/2
=> t = tan x
=> t = tan π/2
=> t = ∞
So, the equation becomes,
I = 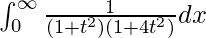
I = 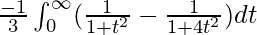
I = ![Rendered by QuickLaTeX.com \frac{-1}{3}\left[tan^{-1}t-2tan^{-1}2t\right]_{0}^{\infty}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-acd2b3023dce5ce06e7340514b4d383f_l3.png)
I = 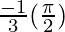
I = 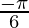
Therefore, the value of 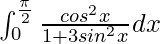 is
is 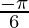 .
.
Question 41. 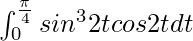
Solution:
We have,
I = 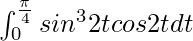
Let sin 2t = u. So, we have
=> 2 cos 2t dt = du
=> cos 2t dt = du/2
Now, the lower limit is, x = 0
=> u = sin 2t
=> u = sin 0
=> u = 0
Also, the upper limit is, x = π/4
=> u = sin 2t
=> u = sin π/2
=> u = 1
So, the equation becomes,
I = 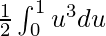
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{u^4}{4}\right]_{0}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e8af27d7948aebde5468385814a36efc_l3.png)
I = 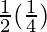
I = 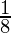
Therefore, the value of 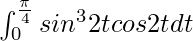 is
is 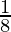 .
.
Share your thoughts in the comments
Please Login to comment...