Question 16. A large window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 meters, find the dimensions of the rectangle that will produce the largest area of the window.
Solution:

According to the question
Let us assume l be the length of the rectangle and b be the breadth of the rectangle
The perimeter of the window = 12 m
⇒ (l + 2b) + (l + l) = 12
⇒ 3l + 2b = 12 ……(i)
Mow we find the area of the window (A) = Area of the rectangle + Area of the equilateral △
A = l (12 – 3l / 2) + √3/4 l2
On differentiating w.r.t. l, we get
dA/dl = 6 – 3l + (√3/2)l = 6 – √3(√3 – 1/2)l
For maxima and minima,
Put dA/dl = 0
⇒ 6 – √3(√3 – 1/2)l = 0
⇒ l = 6/{√3(√3 – 1/2) } = 12- (6 – √3)
Now, d2A/dl2 = -√3(√3 – 1/2) = -3 + √3/2
So, l = 12/(6 – √3) is the point of local maxima
So, When l = 12/(6 – √3), the area of the window is maximum
From eq(i), we get
b = (12 – 3l)/2 = [12 – 3{12/(6 – √3)}]/2 = (24 – 6√3)/(6 – √3)
Question 17. Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is 2R/√3. Also, find the maximum volume.
Solution:
According to the question
R be the radius of the sphere
So, let us assume that r and h be the radius and the height of the cylinder

So, according to the image
h = 2 √(R2 – r2)
Now we find the volume of the cylinder is
V = πr2h = 2πr2√(R2 – r2)
On differentiating w.r.t. r, we get
dV/dr = 4πr √(R2 – r2) + 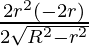
= 4πr √(R2 – r2) – 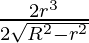
= 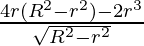
= 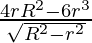
For maxima and minima,
Put dV/dr = 0
4πrR2 – 6πr3 = 0
r2 = 2R2/3
Now, again differentiating w.r.t. r, we get
d2V/dr2 = 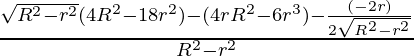
= 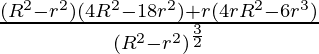
= 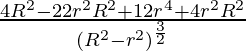
So, at r2 = 2R2/3, d2V/dr2 < 0
Hence, the volume is the maximum when r2 = 2R2/3
so, the height of the cylinder = 2√(R2 – 2R2/3) = 2√(R2/3) = 2R/√3
Hence proved
Question 18. A rectangle is inscribed in a semicircle of radius r with one of its sides on diameter of semicircle. Find the dimensions of the rectangle so that its area is maximum Find also the area.
Solution:
Let us assume EFGH be a rectangle inscribed in a semi-circle. So, r be the radius of the semicircle.
And l and b are the length and width of rectangle.

Now In △OHE,
HE2 = OE2 – OH2
HE = b = 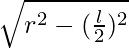 …..(i)
…..(i)
Now we find the area of the EFGH rectangle
A = lb = l × 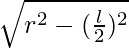
A = 1/2 l √(4r2 – l2)
On differentiating w.r.t. l, we get
dA/dl = 1/2 \sqrt{4r^2-l^2}-\frac{l^2}{\sqrt{4r^2-l^2}}
= 1/2 \frac{4r^2-l^2-l^2}{\sqrt{4r^2-l^2}}
= 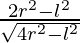
For maxima and minima,
Put dA/dl = 0
⇒ 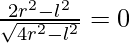
⇒ l = ±√2r
As we know that l can’t be negative so l ≠ -√2r
So, when l = √2r, d2A/dl2 < 0
Hence, the area of the rectangle is maximum when l = √2r
Now put the value of l = √2r in eq(i), we get
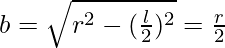
Now we find the area of rectangle = lb
= √2r × r/√2
= r2
Question 19. Prove that a conical tent of given capacity will require the least amount of canvas when the height is √2 times the radius of the base.
Solution:
Let us assume that the radius and height of the cone is r and h.
So, the volume of the cone is
V = 1/3 πr2h
h = 3V/r2 ……(i)
And the surface area of the cone is
A = πrl
Here, l is the slant height = √(r2 + h2)
= πr√(r2 + h2)
= 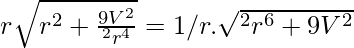
On differentiating w.r.t. r, we get
dA/dr = 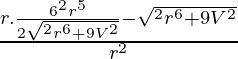
= 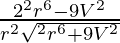
For maxima and minima,
Put dA/dr = 0
2π2r6 = 9V2
r6 = 9V2/2π2
When, r6 = 9V2/2π2, d2S/dr2 > 0
Hence, the surface area of the cone is the least when r6 = 6V2/2π2
Now put r6 = 9V2/2π2 in eq(i), we get
h = 3V/πr2 = 3/πr2(2π2r6/9)1/2 = (3/πr2)(√2πr3/3) = √2r
Hence Proved
Question 20. Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to 2/3 of the diameter of the sphere.
Solution:
Let us assume R be the radius of the sphere

So, from the figure, we get OD = x and AO = OB = R
BD = √(R2 – x2) and AD = (R + x)
Now,
The volume of the cone is
V = 1/3 πr2h
= 1/3 πBD2 × AD
= 1/3 π (R2 – x2) × (R + x)
On differentiating w.r.t. x, we get
dV/dx = π/3 [-2x (R + x) + R2 – x2]
= π/3 [R2 – 2xR – 3x2]
For maximum and minimum
Put dv/dx = 0
⇒ π/3 [R2– 2xR – 3x2] = 0
⇒ π/3 [(R – 3x) (R + x)] = 0
⇒ R – 3x = 0 or x = -R
Here, x = -R is not possible because -r will make the altitude 0
⇒ x = R/3
Now,
d2V/dx2 = π/3[-2R – 6x]
So, when x = R/3, d2v/dx2 = π/3[-2R – 2R] = -4πR/3 < 0
So, x = R/3 is the point of local maxima.
Hence, the volume is maximum when x = R/3
So, the altitude AD = (R + x) = (R + R/3) = 4R/3 = 2/3d
Here, d is the diameter of sphere.
Question 21. Prove that the semi-vertical angle of the right circular cone of given volume and least curved surface is cot-1 (√2).
Solution:

Let us assume h, r and θ be the height, radius and semi vertical angle of the right-angled triangle.
So, the volume of the cone (V) = 1/3 πr2h
⇒ h = 3V/πr2
Slant height of the cone (l) = √(r2 + h2)
l = 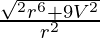
And the curved surface area of the cone is
A = πrl
A = πr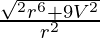
A = 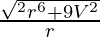
On differentiating w.r.t. r, we get
dA/dr = 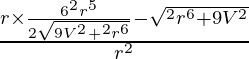
= 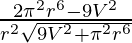
For maximum and minimum
Put dA/dr = 0
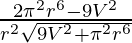 = 0
= 0
⇒ 2π2r6 – 9V2 = 0
⇒ V2 = 2π2r6/9
⇒ V = √2π2r6/9
⇒ V = πr3√2/3
or
r = (3V/π√2)1/3
h/r = √2
cotθ = √2
Semi-vertical angle, θ = cot-1√2
Also, when r < (3V/π√2)1/3, dA/dr < 0
When r > (3V/π√2)1/3, dA/dr > 0
Hence, the curved surface for r = (3V/π√2)1/3 is least.
Question 22 An isosceles triangle of vertical angle 2θ is inscribed in a circle of radius a. Show that the area of the triangle is maximum when θ = π/6.
Solution:

Let us considered ABC is an isosceles triangle such that AB = AC
and the vertical angle∠BAC = 2θ
Radius of the circle = a
Now, draw AM perpendicular to BC.
From the figure we conclude that in △ABC is an isosceles triangle
the circumcenter of the circle lies on the perpendicular from A to BC and
O be the circumcenter of the circle
So, ∠BOC = 2 × 2θ = 4θ
and ∠COM = 2θ [Since △OMB and △OMC are congruent triangles]
OA = OB = OC =a [Radius of the circle]
In △OMC,
CM = asin2θ and OM = acos2θ
BC = 2CM [Perpendicular from the centre bisects the chord]
BC = 2asin2θ …..(i)
In △ABC,
AM = AO + OM
AM = a + acos2θ …..(ii)
Now the area of △ABC is,
A = 1/2 × BC × AM
= 1/2 × 2asin2θ × (a + acos2θ) ……(iii)
On differentiating w.r.t. θ, we get
dA/dθ = a2(2cos2θ + 1/2 × 4cos4θ)
dA/dθ = 2a2 (cos2θ + cos4θ)
Again differentiating w.r.t. θ, we get
d2A/dθ2 = 2a2(-2sin2θ – 4sin4θ)
For maximum and minimum
Put dA/dθ = 0
2a2(cos2θ + cos4θ) = 0
cos2θ + cos4θ = 0
cos2θ + 2cos22θ – 1 = 0
(2cos2θ – 1)(2cos2θ + 1) = 0
cos2θ = 1/2 or cos2θ = -1
2θ = π/3 or 2θ = π
θ = π/6 or θ = π/2
When θ = π/2, it will not form a triangle.
When θ = π/6, d2A/dθ2 < 0
Hence, the area of the triangle is maximum when θ = π/6
Question 23. Find the dimensions of the rectangle of perimeter 36 cm which will sweep out a volume as large as possible when revolved about one of its sides.
Solution:
Let us assume l, b, and V be the length, breadth, and volume of the rectangle.
The perimeter of the rectangle is 36cm
2(l + b) = 36
l + b = 18
l = 18 – b ……(i)
The volume of the cylinder that revolve about the breadth,
V = πl2b
V = π(18 – b )2b
V = π(324 + b2 – 36b)b
V = π(324b + b3 – 36b2)
On differentiating w.r.t. b, we get
dV/db = π(324 + 3b2 – 72b)
Again differentiating w.r.t. b, we get
d2V/db2 = π(6b – 72)
For maximum and minimum
Put dV/db = 0
π(324b + b3 – 36b2) = 0
(b – 6)(b – 18) = 0
b = 6, 18
When b = 6, d2V/db2 = -36π < 0
When b = 18, d2V/db2 = 36π > 0
So, at b = 6 is the maxima
Hence, the volume is maximum when b = 6
Now put the value of b in eq(i), we get
l = 18 – 6
l = 12
Hence, the dimension of rectangle are 12 cm and 6 cm.
Question 24. Show that the height of the cone of maximum volume that can be inscribed in a sphere of radius 12 cm is 16 cm.
Solution:
Let us assume r and h be the radius of the base of cone and height of the cone.

From the figure OD = x, and R = 12, BD = r
In △BOD,
BD = √(R2 – x2)
= √(144 – x2)
= (144 – x2)
and AD = AO + OD
= R + x = 12 + x
The volume of cone is
V = 1/3 πr2h
= 1/3 π BD2 × AD
= 1/3 π(144 – x2)(12 + x)
= 1/3 π(1728 + 144x – 12x2 – x3)
On differentiating w.r.t. x, we get
dV/dx = 1/3π (144 – 24x – 3x2)
For maximum and minimum
Put dV/dx = 0
⇒ 1/3 π(144 – 24x – 3x2) = 0
⇒ x = -12, 4
Here x = -12 is not possible
So, x = 4
Now,
d2V/dx2 = π/3(-24 – 6x)
At x = 4, d2v/dx2 = -2π(4 + x) = -2π × 8 = -16π < 0
So, x = 4 is point of local maxima.
Hence, the height of cone of maximum volume = R + x
= 12 + 4 = 16 cm
Question 25. A closed cylinder has volume 2156 cm3. What will be the radius of its base so that its total surface area is minimum?
Solution:
Given that the volume of the closed cylinder (V) = 2156 cm3
Let us assume r and h be the radius and the height of the cylinder.
So, the volume of the cylinder is
V= πr2h = 2156 …..(i)
and the total surface area is
A = 2πrh + 2πr2
A = 2πr (h + r) …..(ii)
So, from eq (i) and (ii)
A = (2156 × 2)/r + 2πr2
On differentiating w.r.t. r, we get
dA/dr = – 4312/4π + 4πr
For maximum and minimum
Put dA/dr = 0
⇒ (-4312 + 4πr3)/r2 = 0
⇒ r3 = 4312/4π
⇒ r = 7
At r = 7, d2s/dr2 = (8624/r3 + 4π) > 0
So, r = 7 is the point of local minima
Hence, the total surf surface area of closed cylinder will be minimum when r = 7 cm.
Question 26. Show that the maximum volume of the cylinder which can be inscribed in a sphere of radius 5√3 cm is 500π cm3.
Solution:
Let r and h be the radius and height of the cylinder.
Given that R be the radius of the sphere = 5√3

So, from the figure LM = h, OL = x
So, h = 2x
Now, In △AOL,
AL = √(AO2 – OL2)
= √(75 – x2)
As we know that the volume of cylinder is
V = πr2h
= πAL2 × ML
= π(75 – x2) × 2x
On differentiating w.r.t. x, we get
dV/dx = π[150 – 6x2]
For maximum and minimum
Put dV/dx = 0
⇒ π[150 – 6x2] = 0
⇒ x = 5 cm
Also, d2v/dx2 = -12πx
At x = 5, d2v/dx2 = -60πx < 0
So, x = 5 is point of local maxima.
Hence, the volume is maximum when x = 5
So, the maximum volume of cylinder is
= π(75 – 25) × 10 = 500π cm3
Question 27. Show that among all positive numbers x and y with x2 + y2 = r2, the sum x + y is largest when x = y = r/√2.
Solution:
Let us considered the two positive numbers are x and y with
x2+y2 = r2 ……(i)
Let S be the sum of two positive numbers
S = x + y …..(ii)
= x + √(r2 – x2) [From eq(ii)]
On differentiating w.r.t. x, we get
dS/dx = 1 – x/√(r2 – x2)
For maximum and minimum
Put dS/dx = 0
⇒ 1 – x/√(r2 – x2) = 0
⇒ x = √(r2 – x2)
⇒ 2x2 = r2
⇒ x = r/√2, -r/√2
According to the question x and y are the positive numbers
So, x ≠ -r/√2
Now, d2S/dx2 = 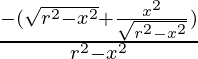
At, x = r/√2, d2S/dx2= ![Rendered by QuickLaTeX.com [\frac{\frac{r}{√2}+\frac{\frac{r^2}{2}}{\frac{r}{√2}}}{\frac{r^2}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1cb880e94514a1e4679356096d10181f_l3.png) < 0
< 0
So, x = r/√2 is point of local maxima.
Hence, the sum is largest when x = y = r/√2
Question 28. Determine the points on the curve x2 = 4y which are nearest to the point (0, 5).
Solution:
The given equation of parabola is
x2 = 4y …….(i)
Let us considered P(x, y) be the nearest point of the given parabola from the point A (0, 5)
Let Q be the square of the distance of P from A
Q = x2 + (y – 5)2 …..(ii)
Q = 4y + (y – 5)2
On differentiating w.r.t. y, we get
⇒ dQ/dy = 4 + 2(y – 5)
For maximum and minimum
Put dQ/dy = 0
⇒ 4 + 2(y – 5) = 0
⇒ 2y = 6
⇒ y = 3
From eq(i), we get
x2 = 12
x = 2√3
⇒ P = (2√3, 3) and p’ = (-2√3, 3)
Now,
d2Q/dy2 = 2 > 0
So, P and P’ are the point of local minima.
Hence, the nearest points are P(2√3, 3) and P”(2√3, 3).
Question 29. Find the point on the curve y2 = 4x which is nearest to the point (2, -8).
Solution:
The given equation of the curve is
y2 = 4x ….(1)
Let us assume P(x, y) be a point on the given curve and
Q be the square of the distance between A(2,-8) and P.
So, Q = (x – 2)2 + (y + 8)2 …….(ii)
= (y2/4 – 2)2 + (y + 8)2
On differentiating w.r.t. y, we get
dQ/dy = 2(y2/4 – 2) × y/2 + 2(y + 8)
= (y3 – 8y)/4 + 2y + 16
= y3/4 + 16
For maximum and minimum
Put dQ/dy = 0
⇒ y3/4 + 16 = 0
⇒ y = -4
Now,
d2Q/dy2 = 3y2/4
At y = -4, d2S/dy2 = 12 > 0
Ao, y = -4 is the point of local minima
Now put the value of y in eq(i), we get
x = y2/4 = 4
Hence, the point is(4, -4) which is nearest to (2, -8).
Question 30. Find the point on the curve x2 = 8y which is nearest to the point (2, 4).
Solution:
The given equation of the curve is
x2 = 8y ….(1)
Let P(x, y) be a point on the given curve, and
Q be the square of the distance between P and A(2, 4).
Q = (x – 2)2 + (y – 4)2 ……..(ii)
= (x – 2)2 + (x2/8 – 4)2
On differentiating w.r.t. x, we get
dQ/dx = 2(x – 2) + 2(x2/8 – 4) × 2x/8
= 2(x – 2) + (x2 – 32)x/16
Also, d2Q/dx2 = 2 + 1/16[x2 – 32 + 2x2]
= 2 + 1/16[3x2 – 32]
For maxima and minima,
dQ/dx = 0
⇒ 2(x – 2) + x(x2 – 32)/16 = 0
⇒ 32x – 64 + x3 -32x = 0
⇒ x3 – 64 = 0
⇒ x = 4
At x = 4, d2Q/dx2 = 2 + 1/16[16 × 3 – 32] = 2 + 1 = 3 > 0
So, x = 4 is point of local minima
Now put the value of x in eq(1), we get
y = x2/8 = 2
So, the P(4, 2) is the nearest point to (2, 4)
Share your thoughts in the comments
Please Login to comment...