Class 12 RD Sharma Solutions – Chapter 21 Areas of Bounded Regions – Exercise 21.1 | Set 2
Last Updated :
20 May, 2021
Question 11. Sketch the region {(x, y) : 9x2 + 4y2 = 36} and find the area enclosed by it, using integration.
Solution:
9×2 + 4y2 = 36


Area of Sector OABCO = ![Rendered by QuickLaTeX.com \displaystyle \int_0^2\sqrt{\frac{36-9x^2}{4}}\ dx\\ =\frac{3}{2}\int_0^2\sqrt{4-x^2}\ dx\\ =\frac{3}{2}\left[\frac{x\sqrt{4-x^2}}{2}+\frac{2^2}{2}sin^{-1}\left(\frac{x}{2}\right)\right]_0^2\\ =\frac{3}{2}\left[\frac{2\sqrt{4-2^2}}{2}+\frac{2^2}{2}sin^{-1}\left(\frac{2}{2}\right)\right]-\frac{3}{2}\left[\frac{0\sqrt{4-0^2}}{2}+\frac{2^2}{2}sin^{-1}\left(\frac{0}{2}\right)\right]\\ =\frac{3}{2}\times2\times\frac{\pi}{2}-0\\ =\frac{3\pi}{2}\ sq.\ units](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bdf39fc937adba83b48121b6dd84b441_l3.png)
Area of the whole figure = 4 x area of DOABCO
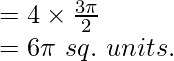
Question 12. Draw a rough sketch of the graph of the function  , x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis
, x ∈ [0, 1] and evaluate the area enclosed between the curve and the x-axis
Solution:
Here, we have to find the area enclosed between the curve and x-axis.
![Rendered by QuickLaTeX.com y=2\sqrt{1-x^2},\ x\ ∈\ [0,\ 1 ]\\ \Rightarrow y^2+4x^2=4,\ x\ ∈\ [0,\ 1]\\ \Rightarrow \frac{x^2}{1}+\frac{y^2}{4},\ x\ ∈\ [0,\ 1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-434207a7f565e59f1b2845c87cb01749_l3.png)
Equation (1) represents an ellipse with centre at origin and passes through (±1, 0) and (0, ±2) and x ∈ [0, 1] as represented by region between y-axis and line x = 1.
Here, is the rough sketch.

Shaded region represents the required area.
We slice it into approximation rectangle of
Width = △x
Length = y
Area of rectangle = y△x
The approx rectangles slide from x = 0 to x = 1,
Thus,
Required area = Region OAPBO
![Rendered by QuickLaTeX.com \displaystyle =\int_0^1y\ dx\\ =\int_0^12\sqrt{1-x^2}\ dx\\ =2\left[\frac{x}{2}\sqrt{1-x^2}+\frac{1}{2}sin^{-1}(x)\right]_0^1\\ =2\left[\left(\frac{1}{2}\sqrt{1-x^2}+\frac{1}{2}sin^{-1}(1)\right)-(0+0)\right]\\ =2\left[0+\frac{1}{2}\times\frac{\pi}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2562246359fb868b0ab589d4a1fc082f_l3.png)
Required area =  square units
square units
Question 13. Determine the area under the curve 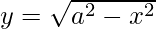 included between the line x = 0 and x = 8.
included between the line x = 0 and x = 8.
Solution:
Here,
We have to find area under the curve
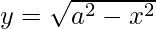
x2 + y2 = a ………..(1)
between x = 0 ………(2)
x = a ………..(3)
Equation (1) represents a circle with Centre (0, 0) and passes axes at (0, ±a), (±a, 0).
Equation (2) represents y-axis and
Equation x = a represents a line parallel to y-axis passing through (a, 0)
Here, is the rough sketch,

Shaded region represents the required area.
We slice it into approximation rectangle of
Width = △x
Length = y
Area of rectangle = y△x
The approx rectangles slide from x = 0 to x = a,
Thus,
Required area = Region OAPBO
![Rendered by QuickLaTeX.com \displaystyle =\int_0^ay\ dx\\ =\int_0^a\sqrt{a^2-x^2}\ dx\\ =\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{a}\right]_0^a\\ =\left[\left(\frac{a}{2}\sqrt{a^2-a^2}+\frac{a^2}{2}sin^{-1}(1)\right)-(0)\right]\\ =2\left[0+\frac{a^2}{2}\times\frac{\pi}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-93ab57e2d3d4ccfe64559fe18dd43043_l3.png)
Required area = 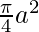 square units
square units
Question 14. Using integration, find the area of the region bounded by the line 2y = 5x + 7, x-axis and the lines x = 2 and x = 8
Solution:
Here,
We have to find area bounded by x-axis
2y + 5x = 7 ………(1)
x = 2 ……..(2)
x = 8 ………(3)
Equation (1) represents line passing through 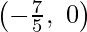 and
and 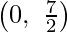 equation.
equation.
Equation (2), (3) shows line parallel to y-axis passing through (2, 0), (8, 0) respectively.
Here, is the rough sketch;

Shaded region represents the required area.
We slice it into approximation rectangle of
Width = △x
Length = y
Area of rectangle = y△x
The approx rectangles slide from x = 2 to x = 8,
Thus,
Required area = Region ABCDA
![Rendered by QuickLaTeX.com \displaystyle =\int_2^8\left(\frac{5x+7}{2}\right)\\ =\frac{1}{2}\left(\frac{5x^2}{2}+7x\right)_2^8\\ =\frac{1}{2}\left[\left(\frac{5(8)^2}{2}+7(8)\right)-\left(\frac{5(2)^2}{2}+7(2)\right)\right]\\ =\frac{1}{2}[(160+56)-(10+14)]\\ =\frac{192}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cabd17649f4c6bce44e0e558c747c18c_l3.png)
Required area = 96 square units
Question 15. Using definite integrals, find the area of the circle x2 + y2 = a2
Solution:
Here, we have to find the area of circle,
x2 + y2 = a2
Equation (1) represents a circle with centre (0, 0) and radius a, Thus is meets the axes (±a, 0), (0, ±a).
Here, is the rough sketch;

Shaded region represents the required area.
We slice it into approximation rectangle of
Width = △x
Length = y
Area of rectangle = y△x
The approx rectangles slide from x = 0 to x = a,
Thus,
Required area = Region ABCDA
= 4 ( Region ABOA)
![Rendered by QuickLaTeX.com \displaystyle =4\int_0^ay\ dx\\ =4\int_0^a\sqrt{a^2-x^2}\ dx\\ =4\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{a}\right]_0^a\\ =4\left[\left(\frac{a}{2}\sqrt{a^2-a^2}+\frac{a^2}{2}sin^{-1}(1)\right)-(0+0)\right]\\ =4\left[0+\frac{a^2}{2}\times\frac{\pi}{2}\right]\\ =4\left(\frac{a^2\pi}{4}\right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9207e9fb74db70a7f579908fc853c36a_l3.png)
Question 16. Using the integration, find the area of the region bounded by the following curves, after making a rough sketch: y = 1 + |x + 1|, x = -2, x = 3, y =
Solution:
Here, we have to find the area enclosed by;
x = -2,
x = 3,
y = 0 and
y = 1 + |x + 1|
⇒ y = 1 + x + 1, if x + 1 0
⇒ y = 2 + x ……….(1), if x ≥ -1
and
⇒ y = 1 – (x + 1), if x + 1 < 0
⇒ y = 1 – x – 1, if x < -1
⇒ y = -x ………(2), if x < -1
Thus,
Equation (1) is a straight line that passes through (0, 2) and (-1 , 1).
Equation (2) is a line passing through (-1, 1) and (-2, 2) and it is enclosed by line x = 2 and x = 3 which are lines parallel to y-axis and pass through (2, 0) and (3, 0) respectively y = 0 is x-axis
Here is the rough sketch

Shaded region represents the required area.
Thus,
Required area = Region (ABECDFA)
Required area = (Region ABEFA + Region ECDFE) ……..(1)
Region ECDFE
We slice it into approximation rectangle of
Width = △x
Length = y1
Area of rectangle = y1△x
The approx rectangles slide from x = -2 to x = -1,
Region ABEFA
We slice it into approximation rectangle of
Width = △x
Length = y2
Area of rectangle = y2△x
The approx rectangles slide from x = -1 to x = 3,
Required area = ![Rendered by QuickLaTeX.com \displaystyle \int_{-2}^{-1}y_1\ dx+\int_{-1}^3y_2\ dx\\ =-\left[\frac{x^2}{2}\right]^{-1}_{-2}+\left[\frac{x^2}{2}+2x\right]_{-1}^3\\ =-\left[\frac{1}{2}+\frac{4}{2}\right]+\left[\left(\frac{9}{2}+6\right)-\left(\frac{1}{2}-2\right)\right]\\ =\frac{3}{2}+\left(\frac{21}{2}+\frac{3}{2}\right)\\ =\frac{27}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ea3a439528ce57e6200a788dd12f7ddc_l3.png)
Required area =  square units
square units
Question 17. Sketch the graph y = |x -5|. Evaluate 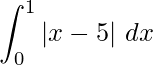 . What does the value of the integral represent on the graph?
. What does the value of the integral represent on the graph?
Solution:
Here, is the sketch of the given graph:
y = |x – 5|

Hence,
Required area = ![Rendered by QuickLaTeX.com \displaystyle =\int_0^1y\ dx\\ =\int_0^1|x-5|\ dx\\ =\int_0^1-(x-5)\ dx\\ =\left[\frac{-x^2}{2}+5x\right]_0^1\\ =\left[-\frac{1}{2}+5\right]\\ =\frac{9}{2}\ sq.\ units](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-126fd5932752b43cada6a73749de8ffb_l3.png)
Thus,
The given integral represents the area bounded by the curves that are,
x = 0,
y = 0,
x = 1
and
y = -(x – 5).
Question 18. Sketch the graph of y = |x + 3| and evaluate 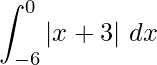 . What does this integral represents on the graph?
. What does this integral represents on the graph?
Solution:
Here,
The given equation is y = |x + 3|
The corresponding values of x and y are given in the following table.
Thus,
After plotting these points,
We will get the graph of y = |x + 3|
It is shown as;

It is known that (x + 3) ≤ 0 for -6 ≤ x ≤ -3 and (x + 3) ≥ 0 for -3 ≤ x ≤ 0
Therefore,
![Rendered by QuickLaTeX.com \displaystyle \int_{-6}^0|(x+3)|\ dx=-\int_{-6}^{-3}(x + 3)\ dx\\ =-\left[\frac{x^2}{2}+3x\right]_{-6}^{-3}+\left[\frac{x^2}{2}+3x\right]_{-3}^0\\ =\left[\left(\frac{(-3)^2}{2}+3(-3)\right)-\left(\frac{(-6)^2}{2}+3(-6)\right)\right]+\left[0-\frac{(-3)^2}{2}+3(-3)\right]\\ =-\left[-\frac{9}{2}\right]-\left[-\frac{9}{2}\right]\\ =9](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f4c2ebae7cc2c8d808cb39f38cd42af4_l3.png)
Question 19. Sketch the graph y = |x + 1|. Evaluate 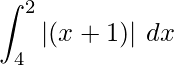 . What does the value of this integral represent on this graph?
. What does the value of this integral represent on this graph?
Solution:
Here,
Given:
y = |x + 1|=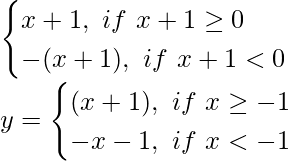
y = x + 1 …………(1)
and
y = -x – 1 ……….(2)
Equation (1) represents a line which meets axes at (0, 1).
Equation (2) represents a line passing through (0, -1) and (-1, 0)
Here is the rough sketch

![Rendered by QuickLaTeX.com \displaystyle \int_{4}^2|(x+1)|\ dx=-\int_{-4}^{-1}(x + 1)\ dx\ +\int_{-1}^2(x+1)\ dx\\ =-\left[\frac{x^2}{2}+x\right]_{-4}^{-1}+\left[\frac{x^2}{2}+x\right]_{-1}^2\\ =-\left[\left(\frac{1}{2}-1\right)-\left(\frac{16}{2}-4\right)\right]+\left[\left(\frac{4}{2}+2\right)-\left(\frac{1}{2}-1\right)\right]\\ =-\left[\left(-\frac{1}{2}-4\right)\right]+\left[4+\frac{1}{2}\right]\\ =\frac{9}{2}+\frac{9}{2}\\ =\frac{18}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25b01443cfbd38702c16b9f38c0a7d42_l3.png)
Required area = 9 square units.
Question 20. Find the area of the region bounded by the curve xy – 3x – 2y – 10 = 0, x-axis and the lines x = 3, x = 4.
Solution:
Here,
We have to find the area bounded by
x axis,
x = 3,
x = 4
and
xy – 3x -2y – 10 = 0
⇒ y(x – 2) = 3x + 10
⇒ 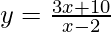
Here, is the rough sketch

Shaded region represents the required area.
We slice it into approximation rectangle of
Width = △x
Length = y
Area of rectangle = y△x
The approx rectangles slide from x = 3 to x = 4,
Required area = Region ABCDA
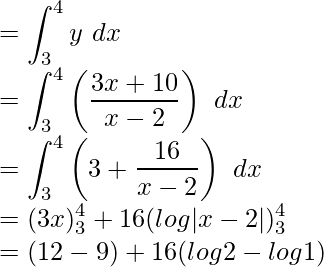
Required area = (3 + 16 log2) square units.
Share your thoughts in the comments
Please Login to comment...