Class 12 RD Sharma Solutions- Chapter 5 Algebra of Matrices – Exercise 5.4
Last Updated :
11 Feb, 2021
Question 1: Let A =  and B =
and B = 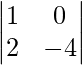 verify that
verify that
(i) (2A)T = 2AT
(ii) (A + B)T = AT + BT
(iii) (A − B)T = AT − BT
(iv) (AB)T = BT AT
Solution:
(i) Given: A =  and B =
and B = 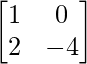
Assume,
(2A)T = 2AT
Substitute the value of A

L.H.S = R.H.S
Hence, proved.
(ii) Given: A =  and B =
and B = 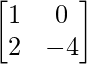
Assume,
(A+B)T = AT + BT

L.H.S = R.H.S
Hence, proved.
(iii) Given: A=  and B=
and B= 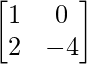
Assume,
(A − B)T = AT − BT
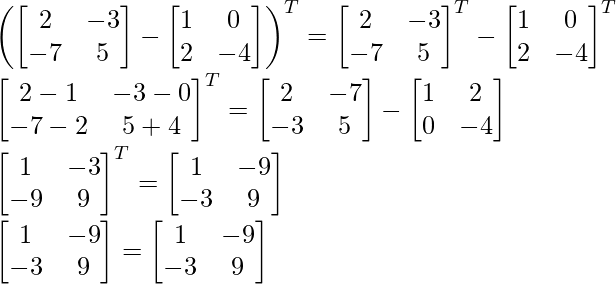
L.H.S = R.H.S
Hence, proved
(iv) Given: A =  and B =
and B = 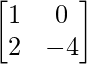
Assume,
(AB)T = BTAT
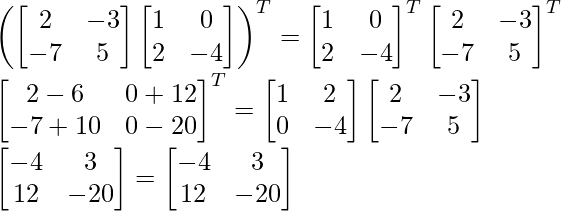
Therefore, (AB)T = BTAT
Hence, proved.
Question 2: A =  and B =
and B = 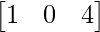 Verify that (AB)T = BTAT
Verify that (AB)T = BTAT
Solution:
Given: A =  and B =
and B = 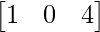
Assume,
(AB)T = BTAT
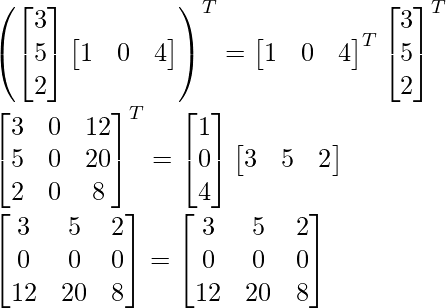
L.H.S = R.H.S
Hence proved
Question 3: Let A = 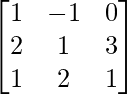 and B =
and B = 
Find AT, BT and verify that
(i) (A + B)T = AT + BT
(ii) (AB)T = BTAT
(iii) (2A)T = 2AT
Solution:
(i) Given: A = 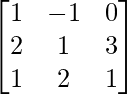
and B = 
Assume
(A + B)T = AT + BT

L.H.S = R.H.S
Hence proved
(ii) Given: A = 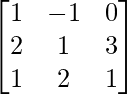 and B =
and B = 
Assume,

(AB)T = BTAT
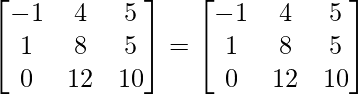
L.H.S =R.H.S
Hence proved
(iii) Given: A = 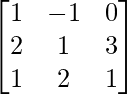 and B =
and B = 
Assume,
(2A)T = 2AT

L.H.S = R.H.S
Hence proved
Question 4: if A =  , B =
, B = 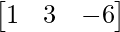 , verify that (AB)T = BTAT
, verify that (AB)T = BTAT
Solution:
Given: A = 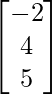 and B =
and B = 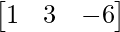
Assume,
(AB)T = BTAT
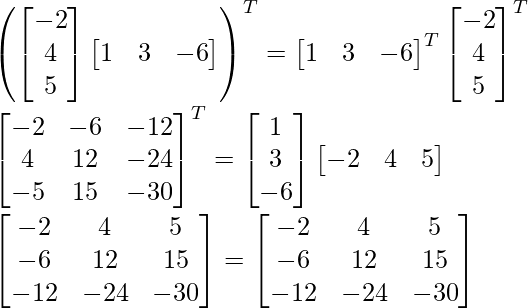
L.H.S = R.H.S
Hence proved
Question 5: If A = 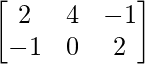 and B =
and B = 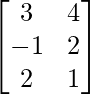 , find (AB)T
, find (AB)T
Solution:
Given: A = 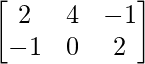 and B =
and B = 
Here we have to find (AB)T
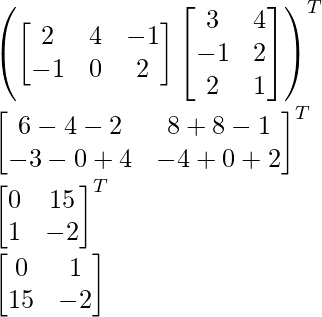
Hence,
(AB)T = 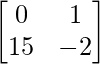
Question 6:
(i) For two matrices A and B, 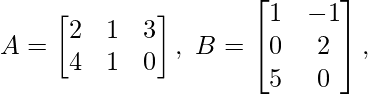 verify that (AB)T = BTAT
verify that (AB)T = BTAT
Solution:
Given,
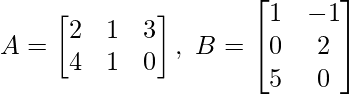
(AB)T = BTAT
⇒ 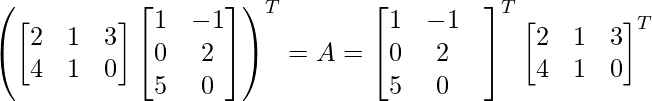
⇒ 
⇒ 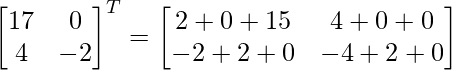
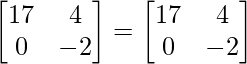
⇒ 
⇒ L.H.S = R.H.S
Hence,
(AB)T = BTAT
(ii) For the matrices A and B, verify that (AB)T = BTAT, where
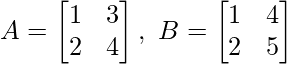
Solution:
Given,
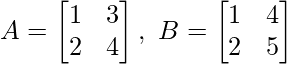
(AB)T = BTAT
⇒ 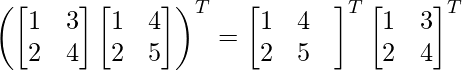
⇒ 
⇒ 
⇒ 
⇒ L.H.S = R.H.s
So,
(AB)T = BTAT
Question 7: Find  , AT – BT
, AT – BT
Solution:
Given that 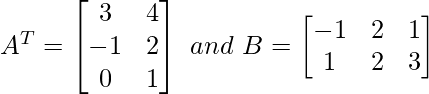
We need to find AT – BT.
Given that, 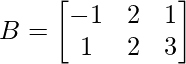
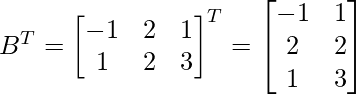
Let us find AT – BT
⇒ 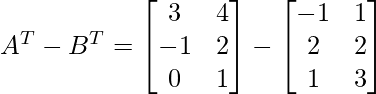
⇒ 
⇒ 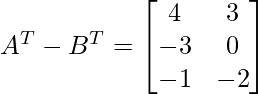
Question 8: If 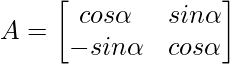 , then verify that A’A = 1
, then verify that A’A = 1
Solution:
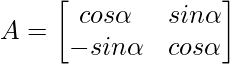

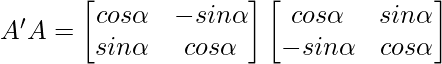
⇒ 
⇒ 
⇒ 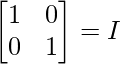
Hence,we have verified that A’A = I
Question 9: 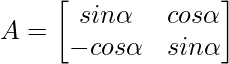 , then verify that A’A = I
, then verify that A’A = I
Solution:
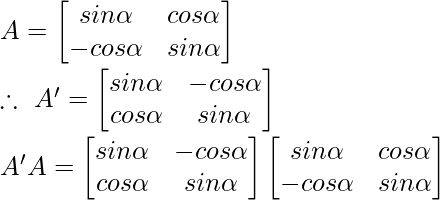
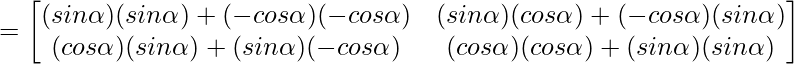
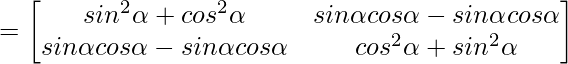
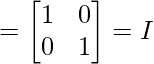
Hence, we have verified that A’A = I
Question 10: If li, mi, ni ; i = 1, 2, 3 denote the direction cosines of three mutually perpendicular vectors in space, prove that AAT = I,
Where 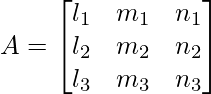
Solution:
Given,
li, mi, ni are direction cosines of three mutually perpendicular vectors
⇒ 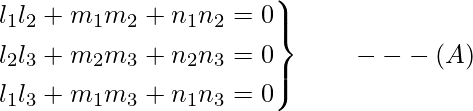
And,
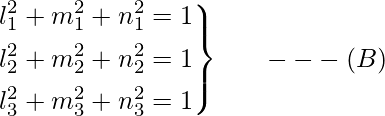
Given,
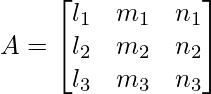
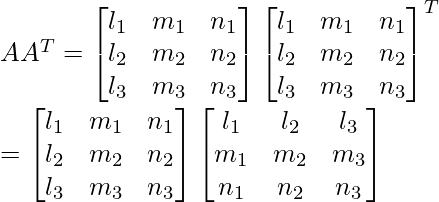

![Rendered by QuickLaTeX.com \begin{bmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{bmatrix}\ \ \ \ \ \ \ [using\ (A)\ and\ (B)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ccbd59993353d1fa11bded80491e24e_l3.png)
= I
Hence,
AAT = I
Share your thoughts in the comments
Please Login to comment...