Question 52. If A =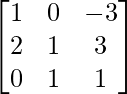 , then verify that A2 + A = A (A + I), where I is the identity matrix.
, then verify that A2 + A = A (A + I), where I is the identity matrix.
Solution:
We have,
A =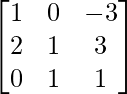
A2 =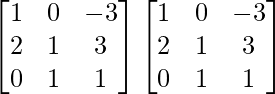
=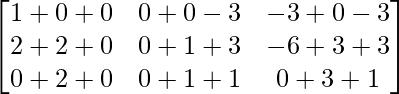
=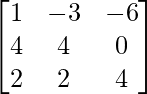
L.H.S. = A2 + A
=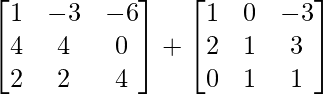
=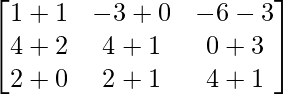
=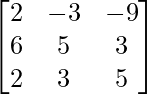
R.H.S. = A (A + I)
=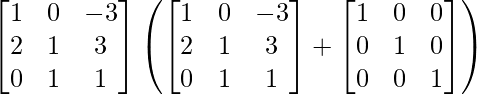
=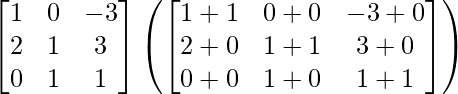
=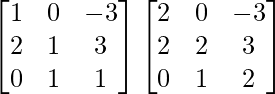
=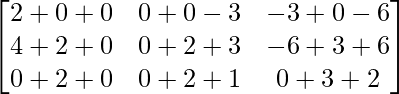
=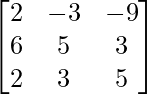
= L.H.S.
Hence proved.
Question 53. If A =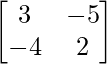 , then find A2 – 5A – 14I. Hence obtain A3.
, then find A2 – 5A – 14I. Hence obtain A3.
Solution:
We have,
A =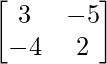
A2 =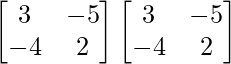
=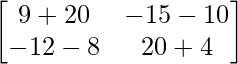
=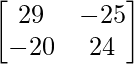
So, A2 – 5A – 14I =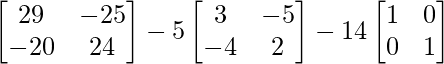
=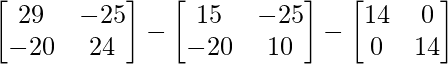
=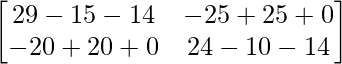
=
= 0
Now, as A2 – 5A – 14I = 0
=> A2 = 5A + 14I
=> A2 A = A (5A + 14I)
=> A3 = 5A2 + 14 AI
=> A3 = 5A2 + 14 A
=> A3 =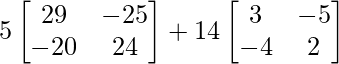
=> A3 =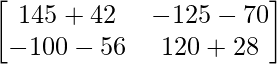
=> A3 =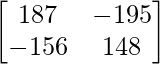
Question 54. Prove the following:
(i) If P(x) =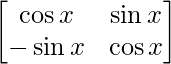 , then show that P(x) P(y) = P(x+y) = P(y) P(x).
, then show that P(x) P(y) = P(x+y) = P(y) P(x).
Solution:
We have,
P(x) =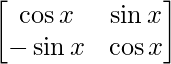
Now, P(x) P(y) =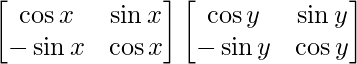
=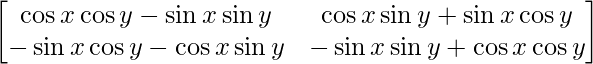
=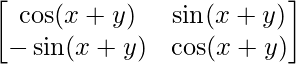
= P(x+y)
Also, P(y) P(x) =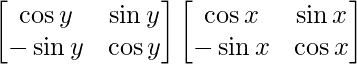
=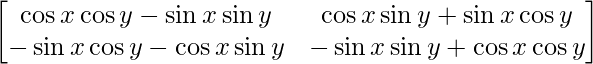
=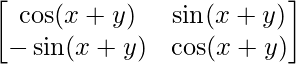
= P(x+y)
Therefore, P(x) P(y) = P(x+y) = P(y) P(x).
Hence proved.
(ii) If P =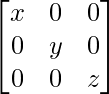 and Q =
and Q =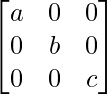 , prove that PQ =
, prove that PQ =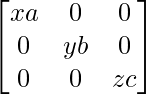 = QP.
= QP.
Solution:
We have,
P =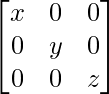 and Q =
and Q =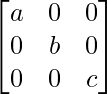
PQ =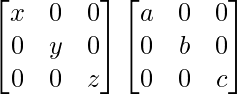
=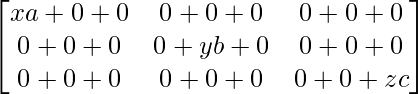
=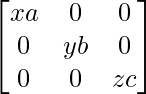
QP =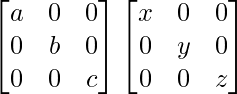
=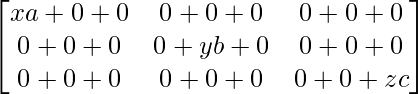
=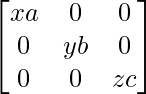
Therefore, PQ =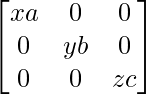 = QP.
= QP.
Hence proved.
Question 55. If A =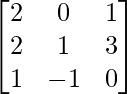 , find A2 – 5A + 4I and find a matrix X such that A2 – 5A + 4I + X = 0.
, find A2 – 5A + 4I and find a matrix X such that A2 – 5A + 4I + X = 0.
Solution:
We have,
A =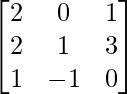
A2 =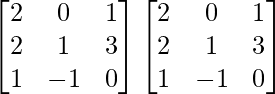
=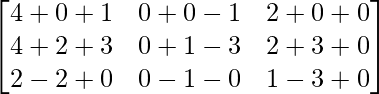
=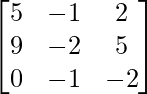
So, A2 – 5A + 4I =
=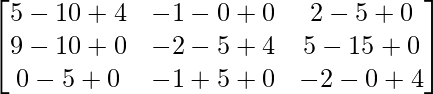
=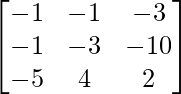
If A2 – 5A + 4I + X = 0, then
=> X = – (A2 – 5A + 4I)
=> X =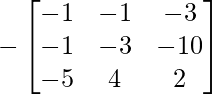
=> X =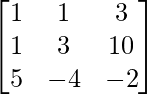
Question 56. If A =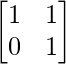 , prove that A =
, prove that A =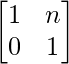 , for all positive integer n.
, for all positive integer n.
Solution:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1 =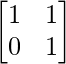
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak =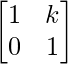
Step 3: For n = k + 1, we have
Ak+1 = Ak A
=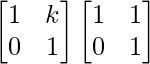
=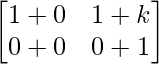
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
Question 57. If A =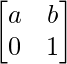 , prove that An =
, prove that An =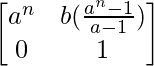 , for every positive integer n.
, for every positive integer n.
Solution:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1 =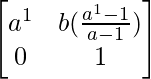
=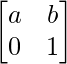
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak =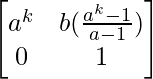
Step 3: For n = k + 1, we have
Ak+1 = Ak A
=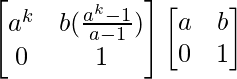
=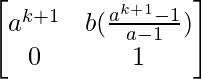
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
Question 58. If A =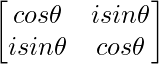 , prove by principle of mathematical induction that An =
, prove by principle of mathematical induction that An =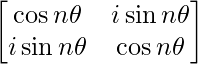 , for all n ∈ N.
, for all n ∈ N.
Solution:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1 =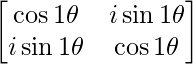
=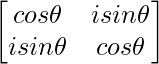
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak =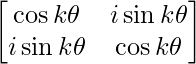
Step 3: For n = k + 1, we have
Ak+1 = Ak A
=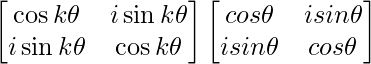
=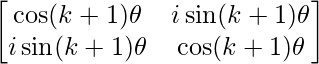
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
Question 59. If A =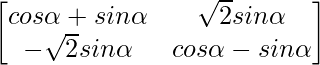 , prove that An =
, prove that An =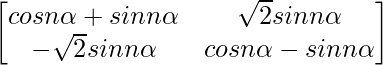 , for all n ∈ N.
, for all n ∈ N.
Solution:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1 =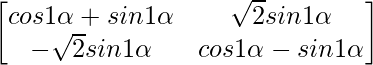
=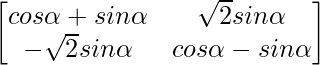
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak =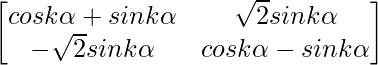
Step 3: For n = k + 1, we have
Ak+1 = Ak A
=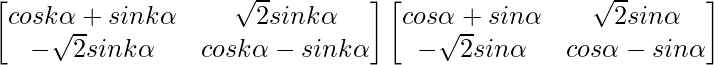
=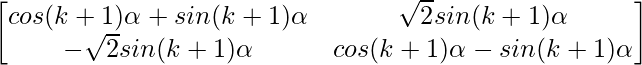
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
Question 60. If A =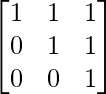 , prove by principle of mathematical induction that An =
, prove by principle of mathematical induction that An =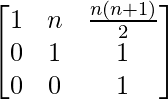 for every positive integer n.
for every positive integer n.
Solution:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1 =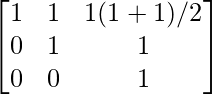
=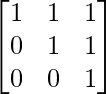
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak =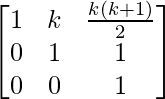
Step 3: For n = k + 1, we have
Ak+1 = Ak A
=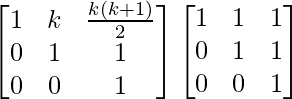
=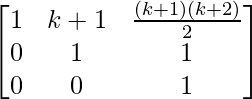
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
Question 61. If B, C are n rowed square matrices and if A = B + C, BC = CB, C2 = 0, then show that for every n ∈ N, An+1 = Bn (B + (n+1)C).
Solution:
We are given,
A = B + C, BC = CB and C2 = 0
=> A2 = (B + C)2
=> A2 = B2 + C2 + 2 BC
=> A2 = B2 + 2 BC
=> A2 = B (B + 2C) . . . . (1)
We have to prove that An+1 = Bn (B + (n+1)C), for n ∈ N
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1+1 = B1 (B + (1+1)C)
A2 = B (B + 2C)
From (1) we get that the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak+1 = Bk (B + (k+1)C)
Step 3: For n = k + 1, we have
Ak+1+1 = Ak+2 = Ak A2
= Bk-1 (B + kC) B (B + 2C)
= Bk (B + kC) (B + 2C)
= Bk (B2 + 2BC + k CB + 2kC2)
= Bk (B2 + 2BC + k BC)
= Bk B (B + (k+2)C)
= Bk+1 (B + (k+2)C)
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
Question 62. If A = diag (a, b, c), show that An = diag (an, bn, cn), for all positive integer n.
Solution:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
A1 = diag (a1, b1, c1)
A = diag (a, b, c)
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
Ak = diag (ak, bk, ck)
Step 3: For n = k + 1, we have
Ak+1 = Ak A
= diag (ak, bk, ck) diag (a, b, c)
=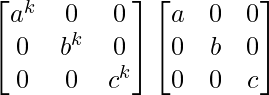
=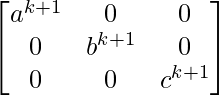
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
Question 63. If A is a square matrix, using mathematical induction prove that (AT)N = (AN)T for all n ∈ N.
Solution:
On using the principle of mathematical induction, we get
Step 1: For n = 1, we have
(AT)1 = (A1)T
AT = AT
So, the result is true for n = 1.
Step 2: Assuming the result is true for n = k, we have
(AT)K = (AK)T
Step 3: For n = k + 1, we have
(AT)K+1 = (AT)K (AT)1
= (AK)T (A1)T
= (AK+1)T
So, the result is also true for n = k+1.
Therefore, the above result is true for all positive integer n.
Hence proved.
Question 64. A matrix X has a + b rows and a + 2 columns while the matrix Y has b + 1 rows and a + 3 columns. Both matrices XY and YX exist. Find a and b. Can you say XY and YX are of the same type? Are they equal?
Solution:
Here X is of order (a+b) × (a+2) and Y is of order (b+1) × (a+3).
If XY exists, we get
=> a + 2 = b + 1 . . . . (1)
And if YX exists, we get
=> a + b = a + 3
=> b = 3
Putting this in (1), we have
=> a + 2 = 3 + 1
=> a = 2
Since the order of the matrices XY and YX is not same, XY and YX are not of the same type and they are unequal.
Question 65. Give an example of matrices A and B such that:
(i) AB ≠ BA
Solution:
Let A =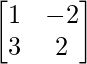 and B =
and B =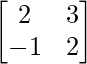
AB =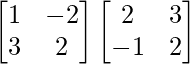
=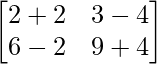
=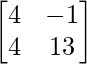
Now, BA =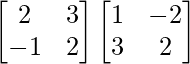
=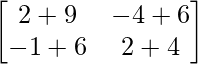
=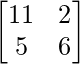
Thus, AB ≠ BA.
(ii) AB = O but A ≠ 0, B ≠ 0
Solution:
Let A =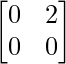 and B =
and B =
AB =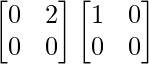
=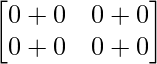
=
Thus, AB = O but A ≠ 0, B ≠ 0.
(iii) AB = O But BA ≠ O
Solution:
Let A =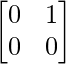 and B =
and B =
Here, AB = 0
But BA =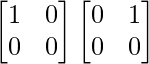
=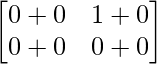
=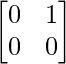
Thus, AB = O but BA ≠ O.
(iv) AB = AC but B ≠ C, A ≠ 0
Solution:
Let A = , B =
, B = and C =
and C =
AB =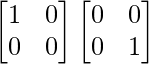
=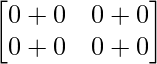
=
And AC =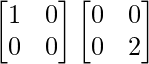
=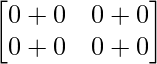
=
Thus, AB = AC but B ≠ C, A ≠ 0.
Question 66. Let A and B be square matrices of the same order. Does (A + B)2 = A2 + 2AB + B2 hold? If not, why?
Solution:
We have,
L.H.S. = (A + B)2
= (A + B) (A + B)
= A (A + B) + B (A + B)
= A2 + AB + BA + B2
Here AB ≠ BA as matrix does not have a commutative property.
Therefore, (A + B)2 ≠ A2 + 2AB + B2.
Question 67. If A and B are square matrices of the same order, explain, why in general
(i) (A + B)2 ≠ A2 + 2AB + B2
Solution:
We have,
L.H.S. = (A + B)2
= (A + B) (A + B)
= A (A + B) + B (A + B)
= A2 + AB + BA + B2
Here AB ≠ BA as in general matrix does not have a commutative property.
Therefore, (A + B)2 ≠ A2 + 2AB + B2.
(ii) (A – B)2 ≠ A2 – 2AB + B2
Solution:
We have,
L.H.S. = (A – B)2
= (A – B) (A – B)
= A (A – B) + B (A – B)
= A2 – AB – BA + B2
Here AB ≠ BA as in general matrix does not have a commutative property.
Therefore, (A – B)2 ≠ A2 – 2AB + B2.
(iii) (A + B) (A – B) ≠ A2 – B2
Solution:
We have,
L.H.S. = (A + B) (A – B)
= A (A – B) + B (A – B)
= A2 – AB + BA – B2
Here AB ≠ BA as in general matrix does not have a commutative property.
Therefore, (A + B) (A – B) ≠ A2 – B2.
Question 68. Let A and B be square matrices of the order 3 × 3. Is (AB)2 = A2 B2? Give reasons.
Solution:
We know, (AB)2 = A2 B2, only if AB = BA
If AB = BA, then
(AB)2 = (AB) (AB)
On using associative law, we get
= A (BA) B
= A (AB) B
= A2 B2
Hence proved.
Question 69. If A and B are square matrices of the same order such that AB = BA, then show that (A + B)2 = A2 + 2AB + B2.
Solution:
We are given, AB = BA.
L.H.S. = (A + B)2
= (A + B) (A + B)
= A (A + B) + B (A + B)
= A2 + AB + BA + B2
= A2 + AB + BA + B2
= A2 + 2AB + B2
= R.H.S.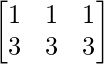
Hence proved.
Question 70. Let A =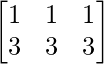 , B =
, B =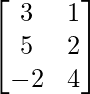 and C =
and C =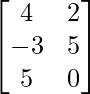 . Verify that AB = AC though B ≠ C, A ≠ O.
. Verify that AB = AC though B ≠ C, A ≠ O.
Solution:
We have,
A =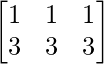 , B =
, B = and C =
and C =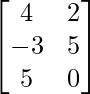
L.H.S. = AB
=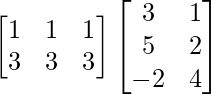
=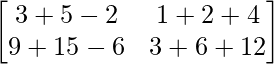
=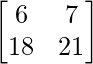
R.H.S. = AC
=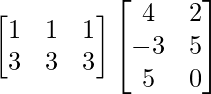
=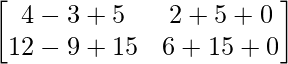
=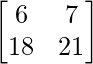
Therefore, L.H.S. = R.H.S.
Hence proved.
Question 71. Three shopkeepers A, B and C go to a store to buy stationary. A purchases 12 dozen notebooks, 5 dozen pens and 6 dozen pencils. B purchases 10 dozen notebooks, 6 dozen pens and 7 dozen pencils. C purchases 11 dozen notebooks, 13 dozen pens and 8 dozen pencils. A notebook costs 40 paise, a pen costs Rs. 1.25 and a pencil costs 35 paise. Use matrix multiplication to calculate each individual’s bill.
Solution:
Cost of notebooks per dozen = (12 × 40) paise = Rs 4.80
Cost of pens per dozen = (12 × 1.25) paise = Rs 15
Cost of Pencils per dozen = (12 × 35) paise = Rs 4.20
So, we get
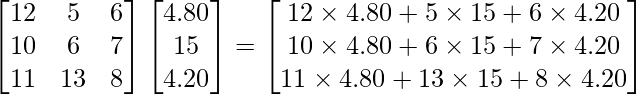
=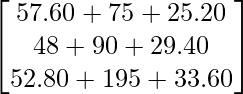
=
Therefore, the bills of A, B and C are Rs 157.80, Rs 167.40 and Rs 281.40, respectively.
Question 72. The cooperative stores of a particular school has 10 dozen physics books, 8 dozen chemistry books and 5 dozen mathematics books. Their selling prices are Rs. 8.30, Rs. 3.45 and Rs. 4.50 each respectively. Find the total amount the store will receive from selling all the items.
Solution:
The stocks of various types of books in the store is given as,
Physics Chemistry Mathematics
X =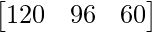
Selling price of various types of books in the store is,
Y =
Total amount received by the store from selling all the items will be = XY
XY =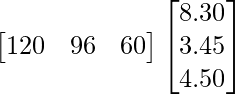
=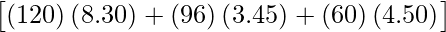
=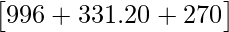
=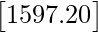
Therefore, the total amount the store will receive from selling all the items is Rs 1597.20.
Question 73. In a legislative assembly election, a political group hired a public relations firm to promote its candidates in three ways: telephone, house calls and letters. The cost per contact (in paise) is given matrix A as
Cost per contact
A =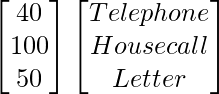
The number of contacts of each type made in two cities X and Y is given in matrix B as
Telephone House call Letter
B =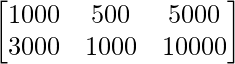
Find the total amount spent by the group in the two cities X and Y.
Solution:
The cost per contact (in paise) is given by
A =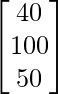
The number of contacts of each type made in the two cities X and Y is given by
Telephone House calls Letter
B =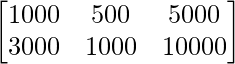
Total amount spent by the group in the two cities X and Y is given by
BA =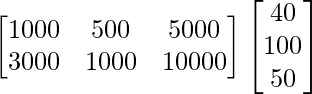
=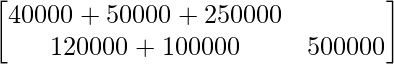
=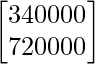
Thus, amount spent on X = Rs 3400 and amount spent on Y = Rs 7200.
Question 74. A trust fund has Rs 30000 that must be invested in two different types of bonds. The first bond pays 5% interest per year, and the second bond pays 7% interest per year. Using matrix multiplication, determine how to divide Rs 30000 among the two types of bonds. If the trust fund must obtain an annual total interest of
(i) Rs 1800
Solution:
Suppose Rs x are invested in the first type of bond and Rs (30000 – x) are invested in the second type of bond, then
A =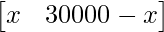 represents investment and the matrix and B =
represents investment and the matrix and B =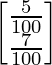 represents rate of interest
represents rate of interest
So, we get
=>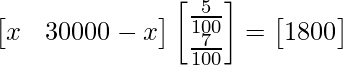
=>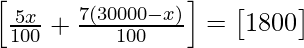
=>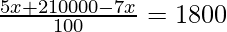
=> 210000 – 2x = 180000
=> 2x = 30000
=> x = 15000
Therefore, amount invested in the first bond = Rs 15000 and amount invested in the second bond = Rs (30000 – 15000) = Rs 15000.
(ii) Rs 2000
Solution:
Suppose Rs x are invested in the first type of bond and Rs (30000 – x) are invested in the second type of bond, then
A =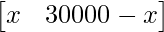 represents investment and the matrix and B =
represents investment and the matrix and B =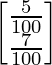 represents rate of interest
represents rate of interest
So, we get
=>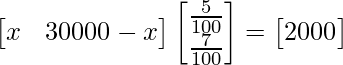
=>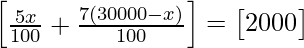
=>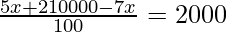
=> 210000 – 2x = 200000
=> 2x = 10000
=> x = 5000
Therefore, amount invested in the first bond = Rs 5000 and amount invested in the second bond = Rs (30000 – 5000) = Rs 25000.
Question 75. To promote making of toilets for women, an organization tried to generate awareness through (i) house calls (ii) letters and (iii) announcements. The cost for each mode per attempt is given below:
i. Rs. 50
ii. Rs. 20
iii. Rs. 40
The number of attempts made in three villages X, Y, and Z are given below:
| | (i) | (ii) | (iii) |
| X | 400 | 300 | 100 |
| Y | 300 | 250 | 75 |
| Z | 500 | 400 | 150 |
Find the total cost incurred by the organization for three villages separately, using matrices.
Solution:
Let A be the matrix showing number of attempts made in three villages X, Y and Z.
A =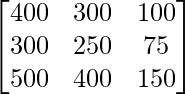
And, suppose B is a matrix showing the cost for each mode per attempt.
B =
AB =
=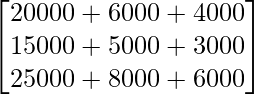
=
Therefore, the total cost incurred by the organisation for three villages X, Y and Z is 30,000 23,000 and 39,000 respectively.
Question 76. There are 2 families A and B. There are 4 men, 6 women and 2 children in family A, and 2 men, 2 women and 4 children in family B. The recommend daily amount of calories is 2400 for men, 1900 for women, 1800 for children and 45 grams of proteins for men, 55 grams for women and 33 grams for children. Represent the above information using matrix. Using matrix multiplication, calculate the total requirement of calories and proteins for each of the two families. What awareness can you create among people about the planned diet from this question?
Solution:
Let X be the matrix showing number of family members in family A and B.
X =
And, suppose Y is a matrix showing the recommend daily amount of calories.
Y =
And, Z be a matrix showing the recommend daily amount of proteins.
Z =
Now, the total requirement of calories of the two families will be shown by XY.
XY =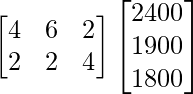
=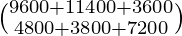
=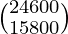
Also, the total requirement of proteins of the two families will be shown by XZ.
XZ =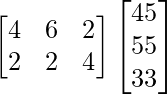
=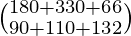
=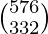
Therefore, the total requirement of calories and proteins for each of the two families is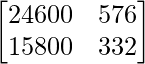 .
.
We must take balanced diet to stay healthy.
Question 77. In a parliament election, a political party hired a public relations firm to promote its candidates in three ways − telephone, house calls and letters. The cost per contact (in paisa) is given in matrix A as
A =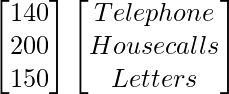
The number of contacts of each type made in two cities X and Y is given in the matrix B as
Telephone House calls Letters
B =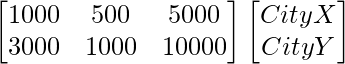
Find the total amount spent by the party in the two cities. What should one consider before casting his/her vote − party’s promotional activity of their social activities?
Solution:
Let A be the matrix showing the cost per contact (in paisa).
A =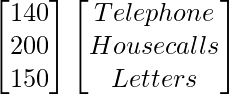
And, B be a matrix showing the number of contacts of each type made in two cities X and Y.
Telephone House calls Letters
B =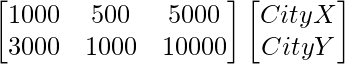
Now, the total amount spent by the party in the two cities will be shown by BA.
BA =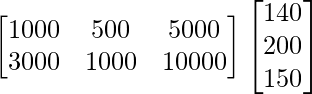
=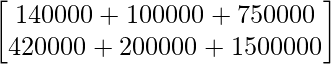
=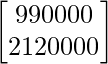
Therefore, the total amount spent by the party in the two cities X and Y is 9900 and 21200 respectively.
One should consider social activities of a party before casting his/her vote to that party.
Share your thoughts in the comments
Please Login to comment...