Class 12 RD Sharma Solutions- Chapter 5 Algebra of Matrices – Exercise 5.1 | Set 2

Last Updated : 03 Jan, 2021

Question 11: Find x, y and z so that A = B, where A= $\begin{bmatrix} x-2 & 3 & 2z\\ 18z & y+2 & 6z \end{bmatrix} = \begin{bmatrix} y & z & 6\\ 6y & x & 2y \end{bmatrix}$ .

Solution:

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁: x-2 = y ………….(eq.1)

a₁₂: z = 3 ………….(eq.2)

a₁₃: 2z = 6 ………….(eq.3)

a₂₁: 18z = 6y ……….(eq.4)

a₂₂: y+2 = x ………..(eq.5)

a₂₃: 6z = 2y …………(eq.6)

From (eq.2) and (eq.3),

=> z = 3

From (eq.4) and (eq.6),

=> y = 3z

=> y = 3(3)

=> y = 9

Substitute ( y=9 ) in (eq.1),

=> x-2 = 9

=>x = 11

Thus x=11, y=9 and z=3.

Question 12: If 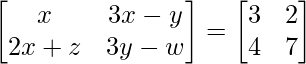$\begin{bmatrix} x & 3x-y\\ 2x+z & 3y-w \end{bmatrix} = \begin{bmatrix} 3 & 2\\ 4 & 7 \end{bmatrix}$ , find x, y, z and w.

Solution:

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁: x = 3 ………….(eq.1)

a₁₂: 3x-y = 2 ………….(eq.2)

a₂₁: 2x+z = 4 ………..(eq.3)

a₂₂: 3y-w = 7 ……….(eq.4)

From (eq.1) ,

=> x = 3

Substitute (x=3) in (eq.2),

=> 3(3)-y = 2

=> y = 3(3) – 2

=> y = 7

Substitute ( x=3 ) in (eq.3),

=> 2(3)+z = 4

=>z = 4-6

=>z = -2

Substitute (y=7) in (eq.4),

=>3(7) – w = 7

=>w = 21 – 7

=>w = 14

Thus x=3, y=7, z=-2 and w=14.

Question 13: If 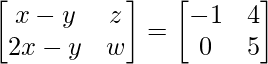$\begin{bmatrix} x-y & z \\ 2x-y & w \end{bmatrix} = \begin{bmatrix} -1 & 4 \\ 0 & 5 \end{bmatrix}$ , find x, y, z and w.

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁: x-y = -1 ………….(eq.1)

a₁₂: z = 4 ………….(eq.2)

a₂₁: 2x-y = 0 ………..(eq.3)

a₂₂: w = 5 …………….(eq.4)

From (eq.2),

=> z = 4

And from (eq.4),

=> w = 5

Now, (eq.1) and (eq.3) form a system of equations comprising of variables x and y.

Thus, (eq.1) – (eq.2),

=> (x-2x) +(-y+y) = -1 – 0

=> -x = -1

=> x = 1

Substitute (x=1) in (eq.1),

=> 1-y = -1

=>y = 2

Thus, x=1, y=2, z=4 and w=5.

Question 14: If 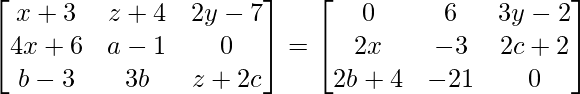$\begin{bmatrix} x+3 & z+4 & 2y-7\\ 4x+6 & a-1 & 0\\ b-3 & 3b & z+2c \end{bmatrix} = \begin{bmatrix} 0 & 6 & 3y-2\\ 2x & -3 & 2c+2\\ 2b+4 & -21 & 0 \end{bmatrix}$ . Obtain the values of a, b, c, x, y and z.

Solution:

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁: x+3 = 0 ……………..(eq.1)

a₁₂: z+4 = 6 ………….(eq.2)

a₁₃: 2y-7 = 3y-2 ……..(eq.3)

a₂₁: 4x+6 = 2x ………….(eq.4)

a₂₂: a-1 = -3 ……………..(eq.5)

a₂₃: 0 = 2c+2 …………….(eq.6)

a₃₁: b-3 = 2b+4…………(eq.7)

a₃₂: 3b = -21………………(eq.8)

a₃₃: z+2c = 0………………(eq.9)

From (eq.1) and (eq.4),

=> x = -3

From (eq.2) ,

=> z+4 = 6

=> z = 2

From (eq.3),

=> 2y-7 = 3y-2

=> 3y-2y = -7+2

=> y = -5

From (eq.5),

=> a = -3+1

=> a = -2

From (eq.8),

=> 3b = -21

=> b = -7

Substitute (z=2) in (eq.9),

=> 2+ 2c = 0

=> c = -1

Thus, x=-3, y=-5, z=2, a=-2, b=-7 and c=-1.

Question 15: If 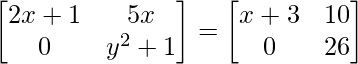$\begin{bmatrix} 2x+1 & 5x \\ 0 & y^2+1 \end{bmatrix} = \begin{bmatrix} x+3 & 10 \\ 0 & 26 \end{bmatrix}$ , find the value of (x+y).

Solution:

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁: 2x+1 = x+3………..(eq.1)

a₁₂: 5x = 10 ………………(eq.2)

a₂₁: 0 = 0 …………………(eq.3)

a₂₂: y²+1 = 26 …………(eq.4)

From (eq.1) and (eq.2),

=> 2x+1 = x+3

=> x=2

From (eq.4),

=> y²+1 = 26

=> y² = 25

=> y = ± 5

Thus if y = +5,

=> x+y = 7

And if y = -5,

=> x+y = -3

Question 16: If $\begin{bmatrix} xy & 4 \\ z+6 & x+y \end{bmatrix} = \begin{bmatrix} 8 & w \\ 0 & 6 \end{bmatrix}$ , then find the values of x, y, z and w.

Solution:

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁: xy = 8 ……………..(eq.1)

a₁₂: 4 = w ………………(eq.2)

a₂₁: z+6 = 0 …………..(eq.3)

a₂₂: x+y = 6 …………..(eq.4)

From (eq.2),

=> w = 4

And from (eq.3),

=> z = -6

Now, we can see that (eq.1) and (eq.4) form a system of equations comprising of variables x and y.

From (eq.1),

=> x = 8/y

Substitute (x=8/y) in (eq.4):

=> y + (8/y) = 6

=> y² – 6y +8 = 0

Solving the above equation,

=> y² – 4y – 2y + 8 = 0

=> y( y-4 ) -2( y-4 ) = 0

=> (y – 2)(y – 4) = 0

=> y = 2 or 4

Substitute in (eq.1):

=> when x=2, y=4 and when x=4, y=2.

Thus, (x,y) = (2,4) or (4,2) and z = -6 and w = 4.

Question 17(i): Give an example of a row matrix which is also a column matrix.

Solution:

We know the order of a row matrix can be written as 1xn (1 row with n elements).

And similarly, the order of a column matrix is mx1.

So, a row matrix which is also a column matrix must be of the order (1×1).

As an example, we can take the matrix : 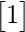$\begin{bmatrix} 1 \end{bmatrix}$

Question 17(ii): Give an example of a diagonal matrix which is not scalar.

Solution:

In a diagonal matrix, only the diagonal elements possess non-zero values. Thus, for a nxn diagonal matrix, a_ii ≠ 0, for 1≤ i ≤ n.

And a scalar matrix is a diagonal matrix, such that all the diagonal elements are equal.

Thus, a matrix which is diagonal but not scalar is:

$\begin{bmatrix} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 3 \end{bmatrix}$

Question 17(iii): Give an example of a triangular matrix.

Solution:

A triangular matrix is a square matrix, and it is filled in such a way that, either the triangle above the main-diagonal is non-zero (upper-triangular) or the triangle below the diagonal is non-zero (lower-triangular).

Thus, an example would be : $\begin{bmatrix} 1 & 2 & 3\\ 0 & 1 & 4\\ 0 & 0 & 1 \end{bmatrix}$

Question 18: The sales figure of two car dealers during January 2013 showed that dealer A sold 5 deluxe, 3 premium and 4 standard cars, while dealer B sold 7 deluxe, 2 premium and 3 standard cars. Total sales over the month period of January- February revealed that dealer A sold 8 deluxe, 7 premium and 6 standard cars. In the same 2 month period, dealer B sold 10 deluxe, 5 premium and 7 standard cars. Write 2×3 matrices summarizing sales data for January and 2-month period for each dealer.

Solution:

The above data can be represented in the form of tables:

For January 2013,

Deluxe Premium Standard
Dealer A 5 3 4
Dealer B 7 2 3

For January to February,

Deluxe Premium Standard
Dealer A 8 7 6
Dealer B 10 5 7

Thus, the two matrices are : 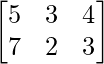$\begin{bmatrix} 5 & 3 & 4\\ 7 & 2 & 3 \end{bmatrix}$ and $\begin{bmatrix} 8 & 7 & 6\\ 10 & 5 & 7 \end{bmatrix}$

Question 19: For what value of x and y are the following matrices equal?

A=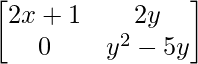 $\begin{bmatrix} 2x+1 & 2y \\ 0 & y^2-5y \end{bmatrix}$ and B =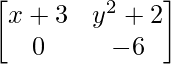 $\begin{bmatrix} x+3 & y^2+2 \\ 0 & -6 \end{bmatrix}$

Solution:

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁: 2x+1 = x+3 …………(eq.1)

a₁₂: 2y = y²+2 ……………(eq.2)

a₂₁: 0 = 0 …………………….(eq.3)

a₂₂: y²-5y = -6 …………..(eq.4)

From (eq.1),

=> 2x-x = 3-1

=> x=2

Taking (eq.2), it can be re-written as,

=> y²-2y+2 = 0

=> y = 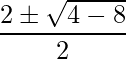$\dfrac {2 \pm \sqrt{4-8}} {2}$

=> y = -1 ± i ( No real solutions )

Taking (eq.4), it can be re-written as,

=> y² – 5y +6 = 0

Solving the equation,

=> y² – 2y – 3y +6 = 0

=> y( y-2 ) -3( y-2 ) = 0

=> ( y-2 )( y-3 ) = 0

=> y = 2 or 3

As values of y are inconsistent, we can say that the above matrices are not equal for any (x,y) pair.

Question 20. Find the values of x and y if 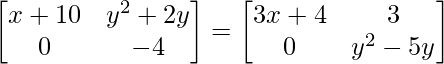$\begin{bmatrix} x+10 & y^2+2y\\ 0 & -4 \end{bmatrix} = \begin{bmatrix} 3x+4 & 3\\ 0 & y^2-5y \end{bmatrix}$ .

Solution:

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁: x+10 = 3x+4 …………(eq.1)

a₁₂: y²+2y = 3 ……………(eq.2)

a₂₁: 0 = 0 ……………………..(eq.3)

a₂₂: y²-5y = -4 …………..(eq.4)

From (eq.1),

=> 2x = 6

=> x = 3

Taking (eq.2), it can be re-written as,

=> y²+2y-3 = 0

=> y²+ 3y -y -3 = 0

=> y( y+3 ) -1( y+3 ) = 0

=> ( y+3 )( y-1 ) = 0

=> y = -3 or 1

Taking (eq.3), it can be re-written as,

=> y²-5y+4 = 0

=> y² -4y -y +4 =0

=> y( y-4 ) -1( y-4 ) = 0

=> ( y-4 )( y-1 ) = 0

=> y = 4 or 1

The value of y that can satisfy both (eq.2) and (eq.3) is 1.

=> y=1

Thus, x=3 and y=1.

Question 21. Find the values of a and b if A = B , where A=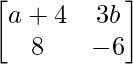 $\begin{bmatrix} a+4 & 3b\\ 8 & -6 \end{bmatrix}$ , B= $\begin{bmatrix} 2a+2 & b^2+2\\ 8 & b^2-5b \end{bmatrix}$ .

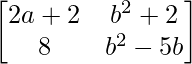Solution:

As it is given that the matrices are equal, every element at a given index on the Left Hand Side (LHS) must be equal to the element at the same index on the Right Hand Side (RHS).

Thus,

a₁₁: a+4 = 2a+2 …………..(eq.1)

a₁₂: 3b = b²+2 …………..(eq.2)

a₂₁: 8 = 8 ……………………..(eq.3)

a₂₂: -6 = b²-5b ………….(eq.4)

From (eq.1),

=> a = 2

Taking (eq.2), it can be re-written as,

=> b²-3b+2=0

=> b² – 2b -b +2 = 0

=> b(b-2) -1(b-2) = 0

=> (b-2)(b-1) = 0

=> b=1 or 2

Taking (eq.4) it can be re-written as,

=> b² -5b +6 = 0

=> b² – 3b -2b + 6 = 0

=> b( b-3 ) -2( b-3 ) = 0

=> ( b-3 )( b-2 ) = 0

=> b = 2 or 3

Thus, b=2 can satisfy both (eq.2) and (eq.4).

=> b = 2

Thus, a=2 and b=2.

Suggest improvement

Class 12 RD Sharma Solutions - Chapter 5 Algebra of Matrices - Exercise 5.1 | Set 1

Class 12 RD Sharma Solutions - Chapter 5 Algebra of Matrices - Exercise 5.2 | Set 1

Share your thoughts in the comments

	Deluxe	Premium	Standard
Dealer A	5	3	4
Dealer B	7	2	3

Chapter 1: Relations

Chapter 2: Functions

Chapter 3: Binary Operations

Chapter 4: Inverse Trigonometric Functions

Chapter 5: Algebra of Matrices

Chapter 6: Determinants

Chapter 7: Adjoint and Inverse of a Matrix

Chapter 8: Solutions of Simultaneous Linear Equations

Chapter 9: Continuity

Chapter 10: Differentiability

Chapter 11: Differentiation

Chapter 12: Higher Order Derivatives

Chapter 13: Derivative as a Rate Measurer

Chapter 14: Differentials, Errors, and Approximations

Chapter 15: Mean Value Theorems

Chapter 16: Tangents and Normals

Chapter 17: Increasing and Decreasing Functions

Chapter 18: Maxima and Minima

Chapter 19: Indefinite Integrals

Chapter 20: Definite Integrals

Chapter 21: Areas of Bounded Regions

Chapter 22: Differential Equations

Chapter 23: Algebra of Vectors

Chapter 24: Scalar Or Dot Product

Chapter 25: Vector or Cross Product

Chapter 26: Scalar Triple Product

Chapter 27: Direction Cosines and Direction Ratios

Chapter 28: Straight Line in Space

Chapter 29: The Plane

Chapter 30: Linear programming

Chapter 31: Probability

Chapter 32: Mean and Variance of a Random Variable

Chapter 33: Binomial Distribution

Chapter 1: Relations

Chapter 2: Functions

Chapter 3: Binary Operations

Chapter 4: Inverse Trigonometric Functions

Chapter 5: Algebra of Matrices

Chapter 6: Determinants

Chapter 7: Adjoint and Inverse of a Matrix

Chapter 8: Solutions of Simultaneous Linear Equations

Chapter 9: Continuity

Chapter 10: Differentiability

Chapter 11: Differentiation

Chapter 12: Higher Order Derivatives

Chapter 13: Derivative as a Rate Measurer

Chapter 14: Differentials, Errors, and Approximations

Chapter 15: Mean Value Theorems

Chapter 16: Tangents and Normals

Chapter 17: Increasing and Decreasing Functions

Chapter 18: Maxima and Minima

Chapter 19: Indefinite Integrals

Chapter 20: Definite Integrals

Chapter 21: Areas of Bounded Regions

Chapter 22: Differential Equations

Chapter 23: Algebra of Vectors

Chapter 24: Scalar Or Dot Product

Chapter 25: Vector or Cross Product

Chapter 26: Scalar Triple Product

Chapter 27: Direction Cosines and Direction Ratios

Chapter 28: Straight Line in Space

Chapter 29: The Plane

Chapter 30: Linear programming

Chapter 31: Probability

Chapter 32: Mean and Variance of a Random Variable

Chapter 33: Binomial Distribution

Class 12 RD Sharma Solutions- Chapter 5 Algebra of Matrices – Exercise 5.1 | Set 2

Question 11: Find x, y and z so that A = B, where A= .

Question 12: If , find x, y, z and w.

Question 13: If , find x, y, z and w.

Question 14: If . Obtain the values of a, b, c, x, y and z.

Question 15: If , find the value of (x+y).

Question 16: If , then find the values of x, y, z and w.

Question 17(i): Give an example of a row matrix which is also a column matrix.

Question 17(ii): Give an example of a diagonal matrix which is not scalar.

Question 17(iii): Give an example of a triangular matrix.

Question 19: For what value of x and y are the following matrices equal?

A= and B =

Question 20. Find the values of x and y if .

Question 21. Find the values of a and b if A = B , where A= , B= .

Question 11: Find x, y and z so that A = B, where A= $\begin{bmatrix} x-2 & 3 & 2z\\ 18z & y+2 & 6z \end{bmatrix} = \begin{bmatrix} y & z & 6\\ 6y & x & 2y \end{bmatrix}$ .

Question 12: If $\begin{bmatrix} x & 3x-y\\ 2x+z & 3y-w \end{bmatrix} = \begin{bmatrix} 3 & 2\\ 4 & 7 \end{bmatrix}$ , find x, y, z and w.

Question 13: If $\begin{bmatrix} x-y & z \\ 2x-y & w \end{bmatrix} = \begin{bmatrix} -1 & 4 \\ 0 & 5 \end{bmatrix}$ , find x, y, z and w.

Question 14: If $\begin{bmatrix} x+3 & z+4 & 2y-7\\ 4x+6 & a-1 & 0\\ b-3 & 3b & z+2c \end{bmatrix} = \begin{bmatrix} 0 & 6 & 3y-2\\ 2x & -3 & 2c+2\\ 2b+4 & -21 & 0 \end{bmatrix}$ . Obtain the values of a, b, c, x, y and z.

Question 15: If $\begin{bmatrix} 2x+1 & 5x \\ 0 & y^2+1 \end{bmatrix} = \begin{bmatrix} x+3 & 10 \\ 0 & 26 \end{bmatrix}$ , find the value of (x+y).

Question 16: If $\begin{bmatrix} xy & 4 \\ z+6 & x+y \end{bmatrix} = \begin{bmatrix} 8 & w \\ 0 & 6 \end{bmatrix}$ , then find the values of x, y, z and w.

A= $\begin{bmatrix} 2x+1 & 2y \\ 0 & y^2-5y \end{bmatrix}$ and B = $\begin{bmatrix} x+3 & y^2+2 \\ 0 & -6 \end{bmatrix}$

Question 20. Find the values of x and y if $\begin{bmatrix} x+10 & y^2+2y\\ 0 & -4 \end{bmatrix} = \begin{bmatrix} 3x+4 & 3\\ 0 & y^2-5y \end{bmatrix}$ .

Question 21. Find the values of a and b if A = B , where A= $\begin{bmatrix} a+4 & 3b\\ 8 & -6 \end{bmatrix}$ , B= $\begin{bmatrix} 2a+2 & b^2+2\\ 8 & b^2-5b \end{bmatrix}$ .