Class 12 RD Sharma Solutions – Chapter 23 Algebra of Vectors – Exercise 23.2
Last Updated :
08 May, 2021
Question 1. If P, Q, and R are three collinear points such that 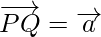 and
and 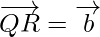 . Find the vector
. Find the vector 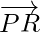
Solution:
According to the question, given that
Points P, Q, and R are collinear.
Also, 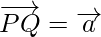 and
and 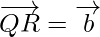
So,
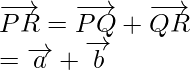
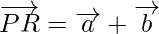
Question 2. Given condition that three vectors 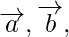 and
and 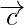 form the three sides of a triangle. What are other possibilities?
form the three sides of a triangle. What are other possibilities?
Solution:
According to the question, given that 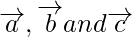 are three sides of a triangle ABC.
are three sides of a triangle ABC.
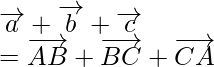
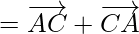 [since
[since 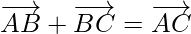 ]
]
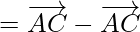 [since
[since 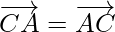 ]
]
So, 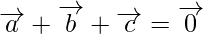
As we know that if vectors are represented in magnitude and direction by the two sides
of triangle taken is same order, then their sum is represented by the third side taken in reverse order.
So,
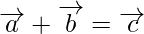
or
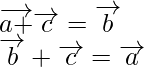
Question 3. If 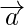 and
and 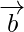 are two non- collinear vectors having the same initial point. What are the vectors represented by
are two non- collinear vectors having the same initial point. What are the vectors represented by 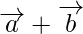 and
and 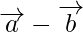 ?
?
Solution:
According to the question, given that 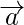 and
and 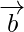
are two non-collinear vectors having the same initial point.
So, let us considered 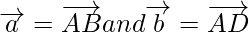
Now we draw a parallelogram named as ABCD
Using the properties of parallelogram, we get
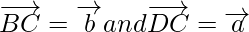
In ∆ABC,
Using the triangle law, we get
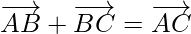
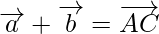 …….(i)
…….(i)
In ∆ABD,
Using the triangle law, we get
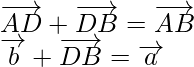
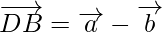 …….(ii)
…….(ii)
On solving equation (i) and (ii), we get
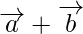 and
and 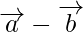
are diagonals of a parallelogram whose adjacent sides are 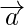 and
and 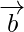
Question 4. If 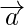 is a vector and m is a scalar such that
is a vector and m is a scalar such that 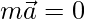 , then what are the alternatives for m and
, then what are the alternatives for m and 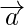 ?
?
Solution:
According to the question, given that m is a scalar and 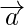 is a vector such that
is a vector such that
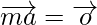
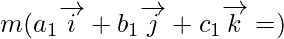 [since let
[since let 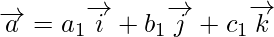 ]
]
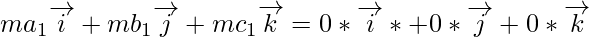
Now on comparing the coefficients of 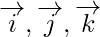 of LHS and RHS, we get
of LHS and RHS, we get
ma1 = 0 ⇒ m = 0 or a1 = 0 …….(i)
mb1 = 0 ⇒ m = 0 or b1 = 0 …….(ii)
mc1 = 0 ⇒ m = 0 or c1 = 0 …….(iii)
Now from eq (i), (ii) and (iii), we get
m = 0 or a1 = b1 = c1 = 0
m = 0 or 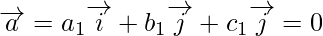
m = 0 or 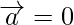
Question 5. If 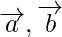 are two vectors, then write the truth value of the following statement:
are two vectors, then write the truth value of the following statement:
(i)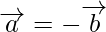 ⇒
⇒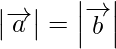
(ii)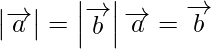
(iii)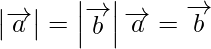
Solution:
(i) Let us assume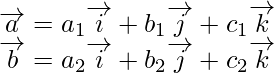
Given that, a = -b
So,
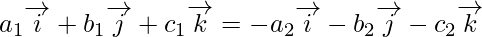
Now on comparing the coefficients of i, j, k in LHS and RHS, we get
a1 = a2 …….(i)
b1 = b2 …….(ii)
c1 = c2 …….(iii)
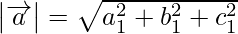
From eq(i), (ii), and (iii),
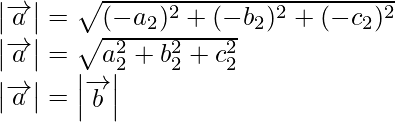
(ii) Given a and b are two vectors such that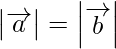
So, it means the magnitude of vector 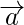 is equal to the magnitude
is equal to the magnitude
of vector 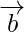 , but we cannot find the direction of the vector.
, but we cannot find the direction of the vector.
Hence, it is false that
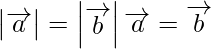
(iii) Given for any vector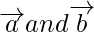
are equal but we cannot find the direction of the vector of 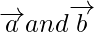
So, it is false.
Question 6. ABCD is a quadrilateral. Find the sum of the vectors 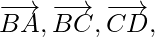 and
and 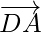 .
.
Solution:
According to the question,
ABCD is a quadrilateral.
so,
In ∆ADC,
By using triangle law, we get
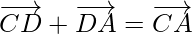 ……(i)
……(i)
In ∆ABC,
By using triangle law, we get
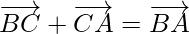 ……(ii)
……(ii)
Now put the value of 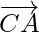 in equation (ii), we get
in equation (ii), we get
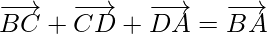
Now on adding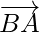 on both sides,
on both sides,
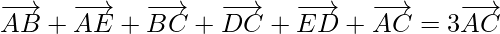
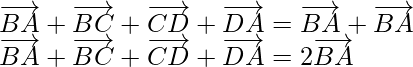
Question 7. ABCDE is a pentagon, prove that
(i)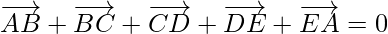
(ii)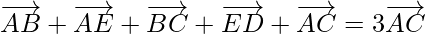
Solution:
(i) According to the question,
ABCDE is a pentagon,
So,
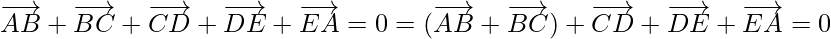
Using the law of triangle 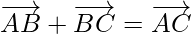 , we get
, we get
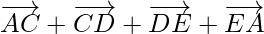
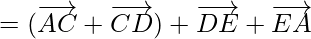
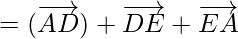
Using triangle law ,![Rendered by QuickLaTeX.com \overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e464380d6f69c9f6d3f269aa41d1c995_l3.png) , we get
, we get
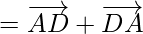
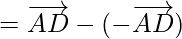
= 0
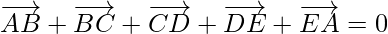
Hence Proved
(ii) According to the question,
ABCDE is a pentagon,
So,
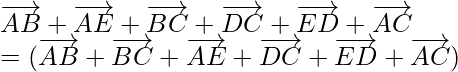
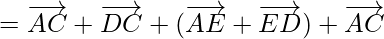
Using triangle law,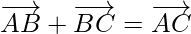 , we get
, we get
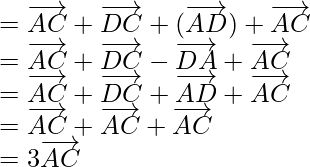
Hence Proved
Question 8. Prove that the sum of all vectors drawn from the centre of a regular octagon to its vertices is the zero vector.
Solution:
Let us assume O be the centre of a regular octagon, as we know that the
centre of a regular octagon bisects all the diagonals passing through it.
So,
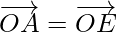 …….(i)
…….(i)
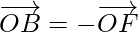 …….(ii)
…….(ii)
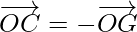 …….(iii)
…….(iii)
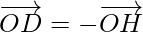 [Tex]\overrightarrow{OD}=-\overrightarrow{OH} [/Tex] …….(iv)
[Tex]\overrightarrow{OD}=-\overrightarrow{OH} [/Tex] …….(iv)
Now on adding equation (i), (ii), and (iv), we get
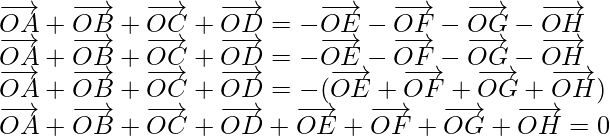
Hence proved
Question 9. If P is a point and ABCD is quadrilateral 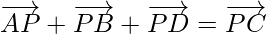 and, show that ABCD is a parallelogram.
and, show that ABCD is a parallelogram.
Solution:
According to the question
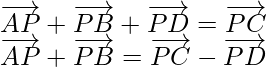

Since, 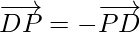
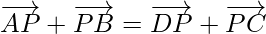
By using triangle law in ∆APB, 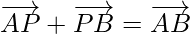
and using triangle law in ∆ DPC, 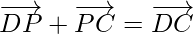
We get
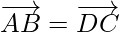
So, AB is parallel to DC and equal is magnitude.
Hence, ABCD is a parallelogram.
Question 10. Five forces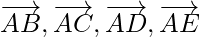 and
and 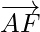 act at the vertex of a regular hexagon ABCDEF. Prove that the resultant is 6
act at the vertex of a regular hexagon ABCDEF. Prove that the resultant is 6 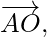 where o is the centre of hexagon.
where o is the centre of hexagon.
Solution:
According to the question,
Prove that
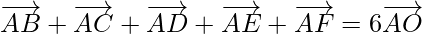
Proof:
As we know that the centre(O) of the hexagon bisects the diagonal 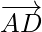
So,
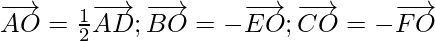
Now,
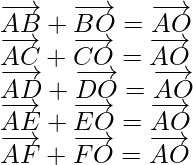
On adding these equations, we get
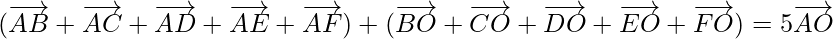
⇒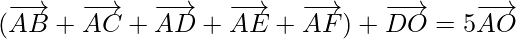
But 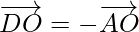
So,
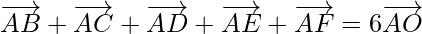
Hence proved
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...