Class 12 RD Sharma Solutions – Chapter 5 Algebra of Matrices – Exercise 5.2 | Set 1
Last Updated :
03 Mar, 2021
Question 1(i): Compute the following sum: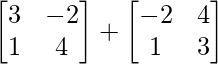 .
.
Solution:
As the matrices are of the same dimensions, we can add them to get a matrix of the same dimensions which is 2×2.
=>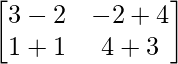
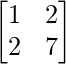
=>
Question 1(ii): Compute the following sum: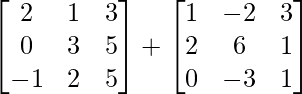 .
.
Solution:
As the matrices are of the same dimensions, we can add them to get a matrix of the same dimensions which is 3×3.
=>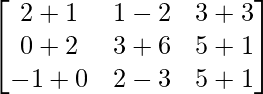
=>
Question 2: Let A =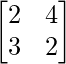 , B =
, B =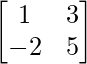 and C =
and C =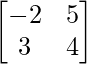 . Find each of the following:
. Find each of the following:
(i): 2A – 3B
Solution:
Both the matrices A and B are of the same order which is 2×2, hence the operation can be performed.
=> 2A =
=> 3B =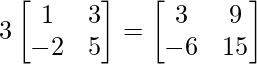
=> 2A – 3B =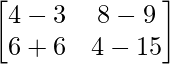
=> 2A – 3B =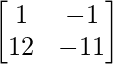
(ii): B – 4C
Solution:
Both the matrices B and C are of the same order which is 2×2, hence the operation can be performed.
=> B =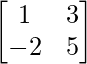
=> 4C =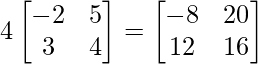
=> B – 4C =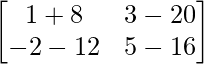
=> B – 4C =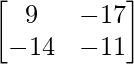
(iii): 3A – C
Solution:
Both the matrices A and C are of the same order which is 2×2, hence the operation can be performed.
=> 3A =
=> C =
=> 3A – C =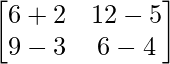
=> 3A – C =
(iv): 3A -2B + 3C
Solution:
The matrices A, B and C are of the same order which is 2×2, hence the operation can be performed.
=> 3A =
=> 2B =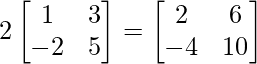
=> 3C =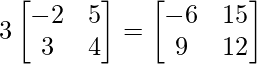
=> 3A – 2B + 3C =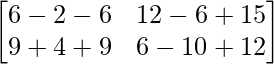
=> 3A – 2B + 3C =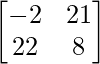
Question 3: If A = , B =
, B =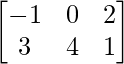 , C =
, C =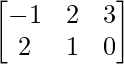 , find:
, find:
(i): A + B and B + C
Solution:
A and B can not be added since A’s order is 2×2 which is different from B’s order which is 2×3.
B+C can be computed and is solved as follows:
=> B + C =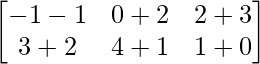
=> B + C =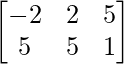
(ii): 2B + 3A and 3C – 4B
Solution:
A and B can not be added since A’s order is 2×2 which is different from B’s order which is 2×3, and thus 2B + 3A can not be calculated.
3C – 4B can be computed and is solved as follows:
=> 3C =
=> 4B =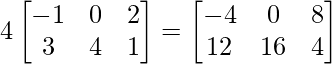
=> 3C – 4B =
=> 3C – 4B =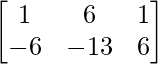
Question 4: Let A =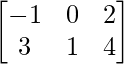 , B =
, B =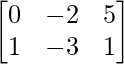 and C =
and C =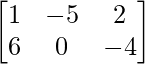 . Compute 2A – 3B + 4C.
. Compute 2A – 3B + 4C.
Solution:
The result can be computed since A, B and C are of the same order which is 2×3.
=> 2A =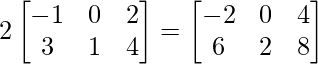
=> 3B =
=> 4C =
=> 2A – 3B + 4C =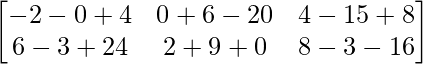
=> 2A – 3B + 4C =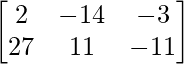
Question 5: If A =diag(2, -5, 9), B = diag(1, 1, -4) and C = diag(-6, 3, 4), find:
(i): A – 2B
Solution:
In the given question A and B are diagonal matrices of the order 3×3, thus the only non-zero elements are present in the diagonal.
=> A = diag(2, -5, 9)
=> 2B = 2. diag(1, 1, -4) = diag(2, 2, -8)
=> A – 2B = diag(2-2, -5-2, 9+8)
=> A – 2B = diag(0, -7, 17)
(ii): B + C – 2A
Solution:
In the given question A, B and C are diagonal matrices of the order 3×3, thus the only non-zero elements are present in the diagonal.
=> B = diag(1, 1, -4)
=> C = diag(-6, 3, 4)
=> 2A = 2. diag(2, -5, 9) = diag(4, -10, 18)
=> B + C – 2A = diag(1-6-4, 1+3+10, -4+4-18)
=> B + C – 2A = diag(-9, 14, -18)
(iii): 2A + 3B – 5C
Solution:
In the given question A, B and C are diagonal matrices of the order 3×3, thus the only non-zero elements are present in the diagonal.
=> 2A = 2. diag(2, -5, 9) = diag(4, -10, 18)
=> 3B = 3. diag(1, 1, -4) = diag(3, 3, -12)
=> 5C = 5. diag(-6, 3, 4) = diag(-30, 15, 20)
=> 2A + 3B – 5C = diag(4+3+30, -10+3-15, 18-12-20)
=> 2A + 3B – 5C = diag(37, -22, -14)
Question 6: Given the matrices A =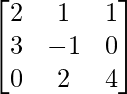 , B =
, B =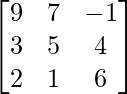 and C =
and C = . Verify that (A + B) + C = A + (B + C).
. Verify that (A + B) + C = A + (B + C).
Solution:
Given L.H.S :
=> (A + B) = 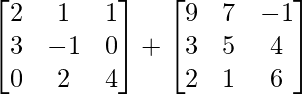
=> (A + B) =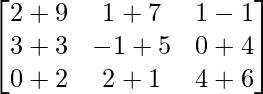
=> (A + B) =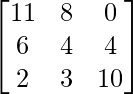
=> (A + B) + C =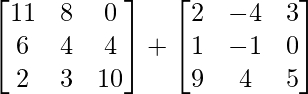
=> (A + B) + C =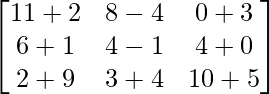
=> (A + B) + C =
Given R.H.S :
=> (B + C) =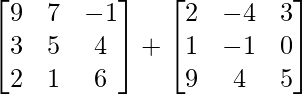
=> (B + C) =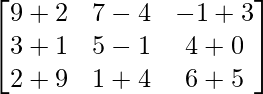
=> (B + C) =
=> A + (B + C) =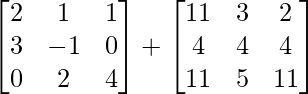
=> A + (B + C) =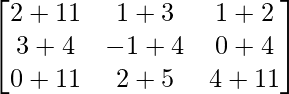
=> A + (B + C) =
Hence R.H.S = L.H.S has been verified.
Question 7: Find the matrices X and Y, if X + Y =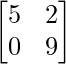 and X – Y =
and X – Y =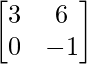 .
.
Solution:
We know that (X + Y) + (X – Y) = 2X.
=> (X + Y) + (X – Y) =
=> 2X =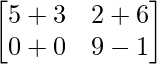
=> 2X =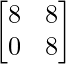
=> X =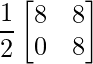
=> X =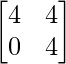
Now Y = (X + Y) – X
=> Y =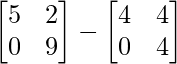
=> Y =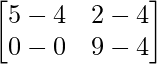
=> Y =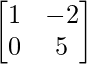
Question 8: Find X, if Y = and 2X + Y =
and 2X + Y =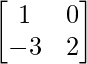 .
.
Solution:
Given 2X + Y =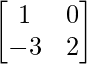
=> 2X + =
=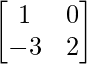
=> 2X =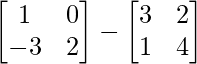
=> 2X =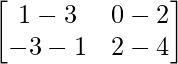
=> 2X =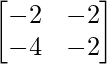
=> X =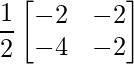
=> X =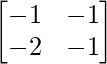
Question 9: Find matrices X and Y, if 2X – Y =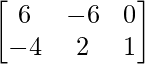 and X + 2Y =
and X + 2Y = .
.
Solution:
We know that 2 (2X – Y) + (X + 2Y) = 4X – 2Y + X + 2Y = 5X .
=> 2 (2X – Y) =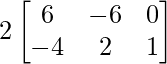
=> 2 (2X -Y) =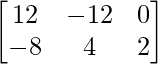
=> 2 (2X – Y) + (X + 2Y) =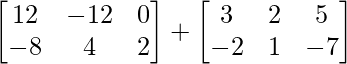
=> 5X =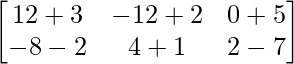
=> 5X =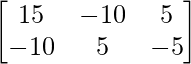
=> X =
=> X =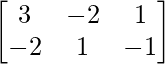
As (X + 2Y) =
=>
=> 2Y =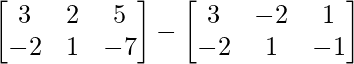
=> 2Y =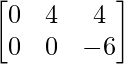
=> Y =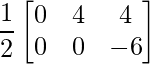
=> Y =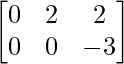
Question 10: If X – Y =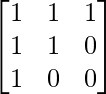 and X + Y =
and X + Y =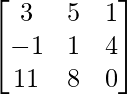 , find X and Y.
, find X and Y.
Solution:
We know that (X + Y) + (X – Y) = 2X.
=> 2X =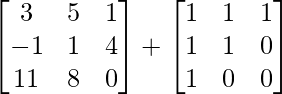
=> 2X =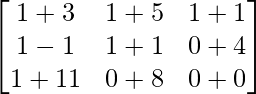
=> 2X =
=> X =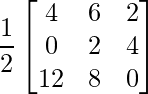
=> X =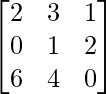
Also (X + Y) – (X -Y) = 2Y.
=> 2Y =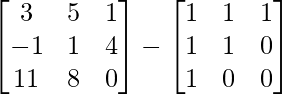
=> 2Y =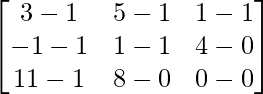
=> 2Y =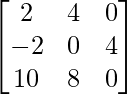
=> Y =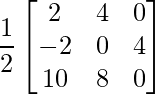
=> Y =
Share your thoughts in the comments
Please Login to comment...