Class 12 RD Sharma Solutions – Chapter 23 Algebra of Vectors – Exercise 23.6 | Set 2
Last Updated :
28 Mar, 2021
Question 11: Find the position vector of the mid-point of the vector joining the points P(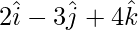 ) and Q(
) and Q( ).
).
Solution:
The mid-point of the line segment joining 2 vectors is given by:
=> 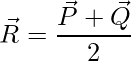
=> 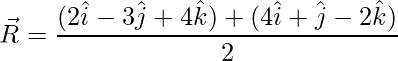
=> 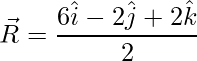
=> 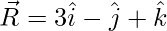
Question 12: Find the unit vector in the direction of the vector 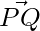 , where P and Q are the points (1,2,3) and (4,5,6).
, where P and Q are the points (1,2,3) and (4,5,6).
Solution:
Let,
=>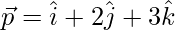
=>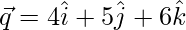
=> 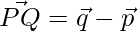
=> 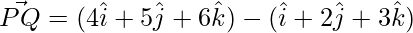
=> 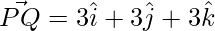
Unit vector is,
=> 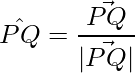
=> 
=> 
=> 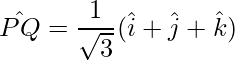
Question 13: Show that the points A(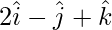 ), B(
), B(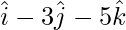 ), C(
), C( ) are the vertices of a right-angled triangle.
) are the vertices of a right-angled triangle.
Solution:
Let,
=> 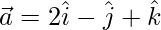
=>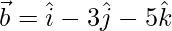
=> 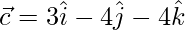
The line segments are,
=> 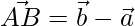
=> 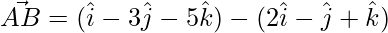
=> 
=> 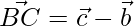
=> 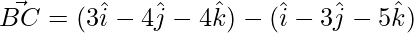
=> 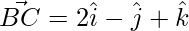
=> 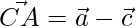
=> 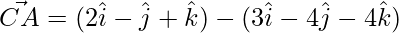
=> 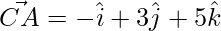
The magnitudes of the sides are,
=> 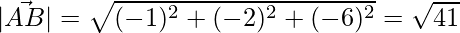
=> 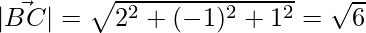
=> 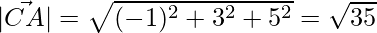
As we can see that 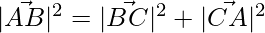
=> Thus, ABC is a right-angled triangle.
Question 14: Find the position vector of the mid-point of the vector joining the points P(2, 3, 4) and Q(4, 1, -2).
Solution:
Let,
=> 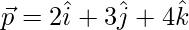
=> 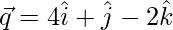
The mid-point of the line segment joining 2 vectors is given by:
=> 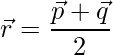
=> 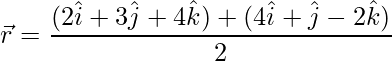
=> 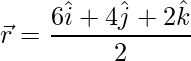
=> 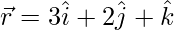
Question 15: Find the value of x for which x(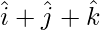 ) is a unit vector.
) is a unit vector.
Solution:
The magnitude of the given vector is,
=> 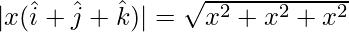
=> 
=> 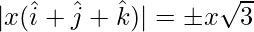
For it to be a unit vector,
=> 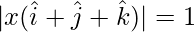
=> 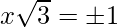
=> 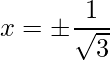
Question 16: If 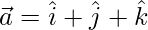 ,
, 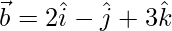 and
and 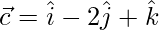 , find a unit vector parallel to
, find a unit vector parallel to 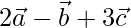 .
.
Solution:
Given, 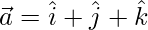 ,
, 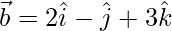 and
and 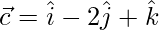
=> 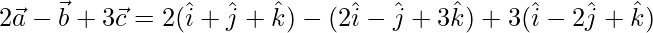
=> 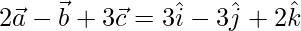
Thus, the unit vector is,
=> 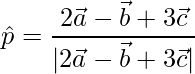
=> 
=> 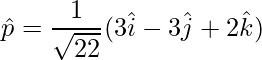
Question 17: If 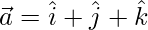 ,
, 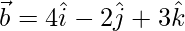 and
and 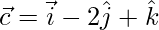 , find a vector of magnitude 6 units which is parallel to the vector
, find a vector of magnitude 6 units which is parallel to the vector 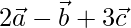 .
.
Solution:
Given, 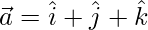 ,
, 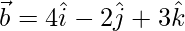 and
and 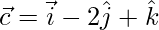
=> 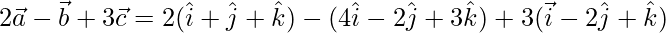
=> 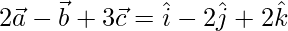
Unit vector in that direction is,
=> 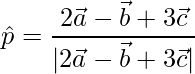
=> 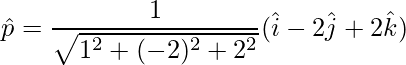
=> 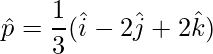
Given that the vector has a magnitude of 6,
=> Required vectors are : 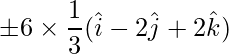 =
= 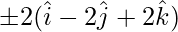
Question 18: Find a vector of magnitude 5 units parallel to the resultant of the vector 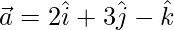 and
and 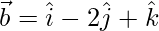 .
.
Solution:
Given, 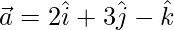 and
and 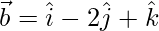
The resultant vector will be given by,
=> 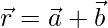
=> 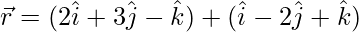
=> 
Unit vector is,
=> 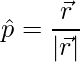
=> 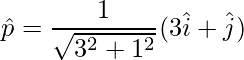
=> 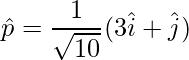
Given that the vector has a magnitude of 5,
=> Required vectors are: 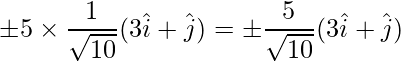
Question 19: The two vectors 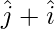 and
and 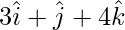 represent the sides
represent the sides 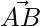 and
and 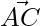 respectively of the triangle ABC. Find the length of the median through A.
respectively of the triangle ABC. Find the length of the median through A.
Solution:
Let D be the point on BC, on which the median through A touches.
D is also the mid-point of BC.
The median 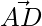 is thus given by:
is thus given by:
=> 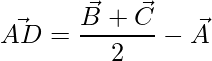
=> 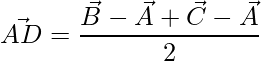
=>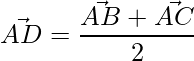
=> 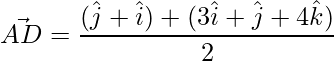
=> 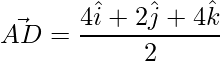
=> 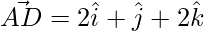
Thus, the length of the median is,
=> 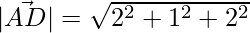
=> 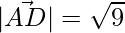
=> 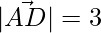 units
units
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...