Class 12 RD Sharma Solutions- Chapter 13 Derivative as a Rate Measurer – Exercise 13.2 | Set 2
Last Updated :
29 May, 2021
Question 17. The top of a ladder 6 meters long is resting against a vertical wall on a level pavement, when the ladder begins to slide outwards. At the moment when the foot of the ladder is 4 meters from the wall, it is sliding away from the wall at the rate of 0.5 m/sec. How fast is the top-sliding downwards at this instance? How far is the foot from the wall when it and the top are moving at the same rate?
Solution:
Let the foot of the ladder be at a distance of x meter from the base of the wall and its top be at a distance of y meter above the ground.

Using Pythagoras Theorem we can get, x2 + y2 = 36
⇒ 2x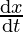 = -2y
= -2y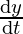 ……………………..(eqn 1)
……………………..(eqn 1)
when x = 4, y = 2√5
⇒ 2 x 4 x 0.5 = -2 x 2√5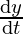
⇒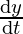 = -1/√5 m/sec
= -1/√5 m/sec
Now using eqn 1, we can write
⇒ 2x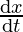 = -2y
= -2y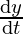
⇒ x = -y
Putting x = -y in x2 + y2 = 36, we get
⇒ 2x2 = 36 ⇒ x = 3 √2 meter
Question 18. A balloon in the form of a right circular cone surmounted by a hemisphere, having a diameter equal to the height of the cone, is being inflated. How fast is its volume changing with respect to its total height h, when h = 9 cm.
Solution:
Let r be the radius of the hemisphere and the cone has height h and volume of the compound arrangement be V, then according to the figure,

⇒ H = h+ r
⇒ H = 3r [Since, h = 2r]
⇒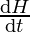 = 3
= 3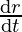 ———————(eqn. 1)
———————(eqn. 1)
Now, volume of the compound arrangement is:
V = 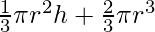
⇒ V = 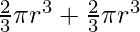 [ h = 2r]
[ h = 2r]
⇒ V = 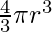
⇒ =
= 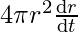
⇒\frac{\mathrm{d} V}{\mathrm{d} t} = \frac{4}{3} \pi r^2 \frac{\mathrm{d} H}{\mathrm{d} t} [using equation 1]
⇒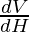 =
= 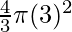
⇒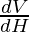 = 12
= 12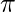 cm3/sec
cm3/sec
Question 19. Water is running into an inverted cone at the rate of π cubic metres per minute. The height of the cone is 10 metres, and the radius of its base is 5 m. How fast the water level is rising when the water stands 7.5 m below the base.
Solution:
Let r be the radius, h be the height and V be the volume of the cone at any time t.

V = πr2h/3
 =
= 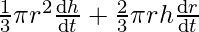
From the image we can conclude,
h = 2r and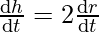
⇒ =
= 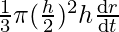 +
+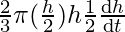
⇒ =
= ![Rendered by QuickLaTeX.com \frac{\pi h^2}{6}\left [ \frac{1}{2}\frac{\mathrm{d} h}{\mathrm{d} t} + \frac{\mathrm{d} h}{\mathrm{d} t} \right ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8b28447f9e43f981bcfce77878823a57_l3.png)
⇒ =
= ![Rendered by QuickLaTeX.com \frac{\pi h^2}{6} \times \left [ \frac{3}{2}\frac{\mathrm{d} h}{\mathrm{d} t} \right ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8a6b55963f6c9320ce4c055b3e59100a_l3.png)
⇒ =
= 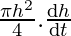
⇒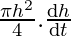 =
= 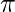
⇒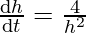
⇒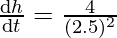
⇒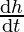 = 0.64 m/min
= 0.64 m/min
Question 20. A man 2 meters high walks at a uniform speed of 6 km/h away from a lamp-post 6 meters high. Find the rate at which the length of his shadow increases ?
Solution:

Since, MNO ∼
MNO ∼ XYO,
XYO,
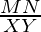 =
= 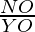
⇒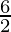 =
= 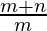
⇒ m/n = 2
⇒ m = 2n
⇒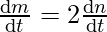
⇒6 = 2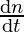
⇒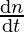 = 3 km/hr
= 3 km/hr
Question 21. The surface area of a spherical bubble is increasing at the rate of 2 cm2/s. When the radius of the bubble is 6 cm, at what rate is the volume of the bubble increasing?
Solution:
Let r, S, V be the radius, surface area, volume of the spherical bubble respectively.
The surface area is increasing, therefore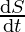 = 2 cm2/s
= 2 cm2/s
Since, surface area of a spherical bubble is given by S = 4πr2
⇒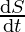 = 8πr
= 8πr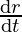
⇒ 2 = 8πx6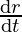
⇒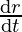 =
= 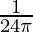 cm/sec
cm/sec
We know, V = 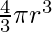
⇒ = 4πr2
= 4πr2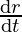
⇒ = 4π x 36 x
= 4π x 36 x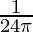
⇒ = 6 cm3/sec
= 6 cm3/sec
Question 22. The radius of a cylinder is increasing at the rate 2 cm/sec. and its altitude is decreasing at the rate of 3 cm/sec. Find the rate of change of volume when radius is 3 cm and altitude 5 cm.
Solution:
Le r be the radius and h be the altitude and V be the volume of the cylinder, then as per given
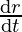 = 2 cm/sec and
= 2 cm/sec and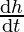 = -3 cm/sec
= -3 cm/sec
Volume of cylinder is given by:
V = πr2h
⇒ = 2πrh
= 2πrh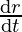 + πr2
+ πr2
⇒ = πr
= πr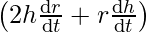
⇒ = π x 3 (2 x 5 x 2 + 2 x (-3) )
= π x 3 (2 x 5 x 2 + 2 x (-3) )
⇒ = 33π cm3/sec
= 33π cm3/sec
Question 23. The volume of metal in a hollow sphere is constant. If the inner radius is increasing at the rate of 1 cm/sec, find the rate of increase of the outer radius when the radii are 4 cm and 8 cm respectively.
Solution:
Let the outer radius be represented by R and inner radius be represented by r. Now, Volume of the hollow sphere is given by
V = ![Rendered by QuickLaTeX.com \frac{4}{3}\pi [R^3 - r^3]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dadab9a10588c77f879bb20c4e6f355d_l3.png)
⇒ = 4π
= 4π![Rendered by QuickLaTeX.com \left [ R^2 \frac{\mathrm{d} R}{\mathrm{d} t} - r^2 \frac{\mathrm{d} r}{\mathrm{d} t} \right ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6b61ea46a0848b08bb39b8b8e09d7514_l3.png)
Since, volume is constant, = 0
= 0
⇒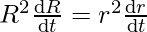
⇒ 64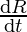 = 16 x 1
= 16 x 1
⇒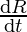 =
= 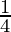 cm/sec
cm/sec
Question 24. Sand is being poured onto a conical pile at the constant rate of 50 cm3/minute such that the height of the cone is always one half of the radius of its base. How fast is the height of the pile increasing when the sand is 5 cm deep ?
Solution:
Let r be the radius, h be the height and V be the volume of conical pile. Now, volume of conical pile is given as:
V = 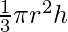
⇒ V = 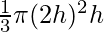 [Since, h = r/2]
[Since, h = r/2]
⇒  =
= 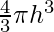
⇒ = 4πh2
= 4πh2
⇒ 50 = 4πh2
⇒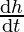 =
= 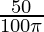
⇒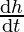 =
= 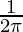 cm/min
cm/min
Question 25.A kite is 120 m high and 130 m of string is out. If the kite is moving away horizontally at the rate of 52 m/sec, find the rate at which the string is being paid out.
Solution:
From the above figure, we can infer using Pythagoras Theorem
MN2 + NO2 = MO2
⇒ x2 + (120) = y2
⇒ 2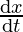 = 2y
= 2y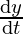
⇒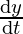 =
= 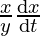
Now, x = 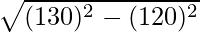 = 50
= 50
⇒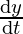 =
= 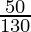 x 52
x 52
⇒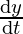 = 20 m/sec
= 20 m/sec
Question 26. A particle moves along the curve y = (2/3)x3 + 1. Find the points on the curve at which the y-coordinate is changing twice as fast as the x-coordinate.
Solution:
Given y = 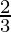 x3 + 1
x3 + 1
⇒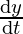 = 2x2
= 2x2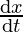
It is also given that, y-coordinate is changing twice as fast as the x-coordinate, therefore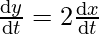
⇒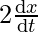 =
= 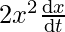
Solving the above equation, we get x = ±1
Substituting the value of x in above given equation y = 5/3 and y = 1/3
So the coordinates of the point are and
and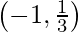
Question 27. Find the point on the curve y2 = 8x for which the abscissa and ordinate change at the same rate?
Solution:
Given, y2 = 8x
⇒ 2y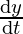 = 8
= 8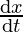
Now, since abscissa and ordinate change at the same rate, therefore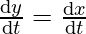
⇒ 2y = 8
⇒ y = 4
Therefore, substituting the value of y in original equation. we get
16 = 8x ⇒ x = 2
Hence, the co-ordinate of the point is (2,4)
Question 28. The volume of a cube is increasing at the rate of 9 cm3/sec. How fast is the surface area increasing when the length of an edge is 10 cm?
Solution:
Let the edge of the cube be denoted by a and its volume be denoted by V.
We know, Volume of cube, V = a3
⇒  = 3a2
= 3a2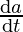
⇒ 9 = 3 x (10)2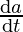
⇒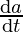 = 0.03 cm/sec
= 0.03 cm/sec
Now, let the surface area of cube be given by A = 6a2
⇒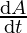 = 12a
= 12a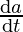
⇒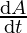 = 12 x 10 x 0.03
= 12 x 10 x 0.03
⇒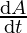 = 3.6 cm2/sec
= 3.6 cm2/sec
Question 29. The volume of a spherical balloon is increasing at the rate of 25 cm3/sec. Find the rate of change of its surface area at the instant when radius is 5 cm?
Solution:
Let r be the radius, V be the volume and S be the surface area of the spherical balloon.
We know, V = 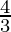 πr3
πr3
⇒ = 4πr2
= 4πr2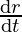
⇒ 25 = 4π (5)2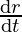
⇒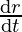 =
= 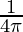 cm/sec
cm/sec
Also, surface area, A = 4πr2
⇒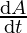 = 8πr
= 8πr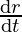
⇒ 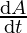 = 8π x 5 x
= 8π x 5 x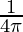
⇒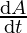 = 10 cm2/sec
= 10 cm2/sec
Question 30. (i) The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of the perimeter ?
(ii) The length x of a rectangle is decreasing at the rate of 5 cm/minute and the width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rates of change of the area of the rectangle ?
Solution:
We are given,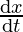 = -5cm/min and
= -5cm/min and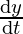 = 4cm/min
= 4cm/min
(i) We know, perimeter of a rectangle P = 2(x + y)
⇒ 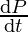 = 2 (
= 2 (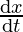 +
+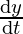 )
)
⇒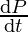 = 2 (-5 + 4)
= 2 (-5 + 4)
⇒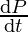 = -2 cm/min
= -2 cm/min
(ii) Also, Area of rectangle A = xy
⇒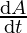 = x
= x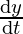 + y
+ y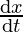
⇒ 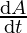 = 8 x 4 + 6 x (-5)
= 8 x 4 + 6 x (-5)
⇒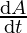 = 2 cm2/min
= 2 cm2/min
Question 31. A circular disc of radius 3 cm is being heated. Due to expansion, its radius increases at the rate of 0.05 cm/sec. Find the rate at which its area is increasing when radius is 3.2 cm.
Solution:
Let r be the radius and A be the area of circular disc respectively.
Then A = πr2
⇒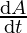 = 2πr
= 2πr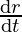
⇒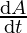 = 2π x 3.2 x 0.05
= 2π x 3.2 x 0.05
⇒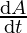 = 0.32π cm2/sec
= 0.32π cm2/sec
Share your thoughts in the comments
Please Login to comment...