Class 12 RD Sharma Solutions – Chapter 25 Vector or Cross Product – Exercise 25.1 | Set 3
Last Updated :
28 Mar, 2021
Question 25. If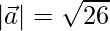 ,
, 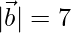 and
and 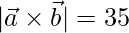 , find
, find 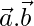
Solution:
We know that,
=> 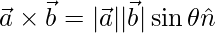
=> 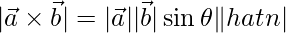
=> 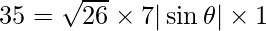
=> 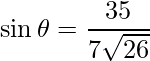
=> 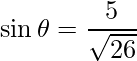
As 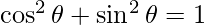 ,
,
=> 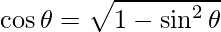
=> 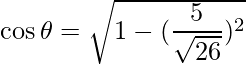
=>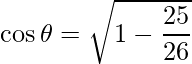
=> 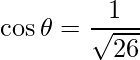
Thus,
=> 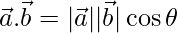
=>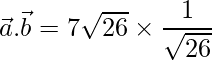
=> 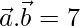
Question 26. Find the area of the triangle formed by O, A, B when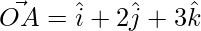 ,
, 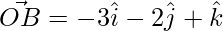
Solution:
The area of a triangle whose adjacent sides are given by  and
and 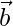 is
is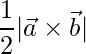
=> 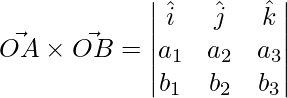
=>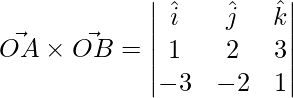
=> ![Rendered by QuickLaTeX.com \vec{OA}\times\vec{OB} = \hat{i}[2+6]-\hat{j}[1+9]+\hat{k}[-2+6]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1678ef9163a101f7f7789f4c0df0b36e_l3.png)
=> 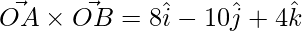
=> Area = 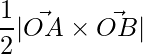
=> Area = 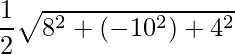
=> Area = 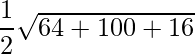
=> Area = 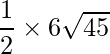
=> Area = 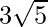 square units.
square units.
Question 27. Let 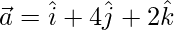 ,
, 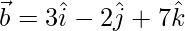 and
and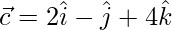 . Find a vector
. Find a vector 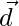 which is perpendicular to both
which is perpendicular to both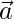 and
and 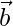 and
and 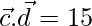
Solution:
Given that 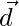 is perpendicular to both
is perpendicular to both  and
and 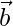 .
.
=> 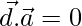 ……….(1)
……….(1)
=> 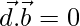 ……….(2)
……….(2)
Also,
=> 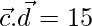 …….(3)
…….(3)
Let 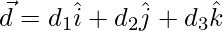
From eq(1),
=> d1 + 4d2 + 2d3 = 0
From eq(2),
=> 3d1 – 2d2 + 7d3 = 0
From eq(3),
=> 2d1 – d2 + 4d3 = 15
On solving the 3 equations we get,
d1 = 160/3, d2 = -5/3, and d3 = -70/3,
=> 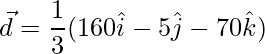
Question 28. Find a unit vector perpendicular to each of the vectors 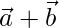 and
and 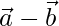 , where
, where 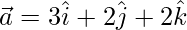 and
and 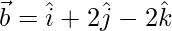 .
.
Solution:
Given that, 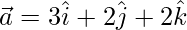 and
and 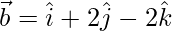
Let 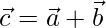
=> 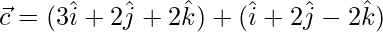
=> ![Rendered by QuickLaTeX.com \vec{c} = \hat{i}[3+1] +\hat{j}[2+2] +\hat{k}[2-2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-480e2d02960c636d243ca37ae89b1c65_l3.png)
=> 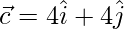
Let 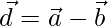
=> 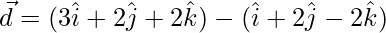
=> ![Rendered by QuickLaTeX.com \vec{d} = \hat{i}[3-1] +\hat{j}[2-2] +\hat{k}[2+2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-938bfcafe06e374b262c5f3bf50d8fda_l3.png)
=>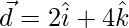
A vector perpendicular to both 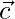 and
and 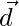 is,
is,
=> 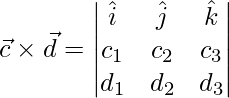
=> 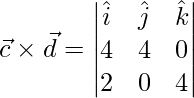
=> ![Rendered by QuickLaTeX.com \vec{c}\times\vec{d} = \hat{i}[16-0]-\hat{j}[16-0]+\hat{k}[0-8]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-14b7d677c3ec1889afa623684a78e0e1_l3.png)
=> 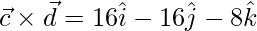
To find the unit vector,
=> 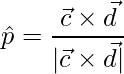
=> 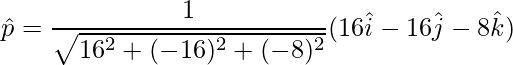
=> 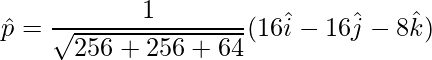
=> 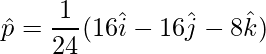
=> 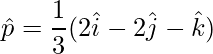
Question 29. Using vectors, find the area of the triangle with the vertices A(2, 3, 5), B(3, 5, 8), and C(2, 7, 8).
Solution:
Given, A(2, 3, 5), B(3, 5, 8), and C(2, 7, 8)
Let,
=>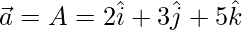
=> 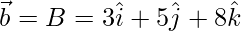
=>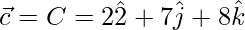
Then,
=> 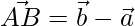
=> 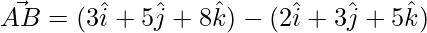
=> ![Rendered by QuickLaTeX.com \vec{AB} = \hat{i}[3-2]+\hat{j}[5-3]+\hat{k}[8-5]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ae4b4c2e504f66c8ceff6185b38e2874_l3.png)
=> 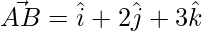
=> 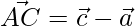
=> 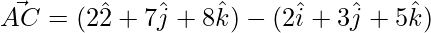
=> ![Rendered by QuickLaTeX.com \vec{AC} = \hat{i}[2-2]+\hat{j}[7-3]+\hat{k}[8-5]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ecb22305add6857ee039a867e360e195_l3.png)
=> 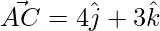
The area of a triangle whose adjacent sides are given by  and
and 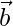 is
is 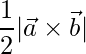
=> 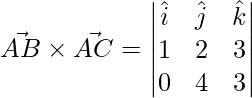
=> ![Rendered by QuickLaTeX.com \vec{AB}\times\vec{AC} = \hat{i}[6-12]-\hat{j}[3-0]+\hat{k}[4-0]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-08e2c2c7868a70bc2ea70b3fd353f02d_l3.png)
=> 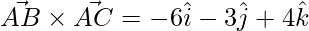
=> Area = 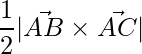
=> Area = 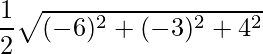
=> Area = √61/2
Question 30. If 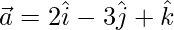 ,
, 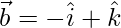 ,
, 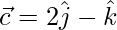 are three vectors, find the area of the parallelogram having diagonals
are three vectors, find the area of the parallelogram having diagonals 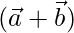 and
and 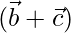 .
.
Solution:
Given, 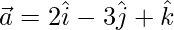 ,
, 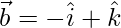 ,
, 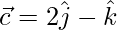
Let,
=> 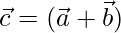
=>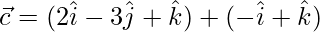
=> 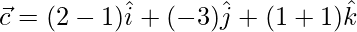
=> 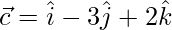
=>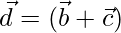
=> 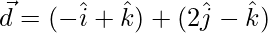
=> 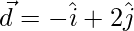
The area of the parallelogram having diagonals 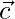 and
and 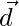 is
is 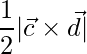
=> 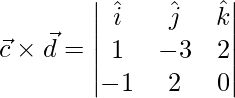
=> ![Rendered by QuickLaTeX.com \vec{c}\times\vec{d} = \hat{i}[0-4] -\hat{j}[0+2]+\hat{k}[2-3]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1c7db8be876706434a270d0dd76480c9_l3.png)
=>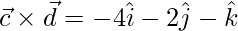
=> Area = 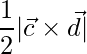
=> Area = 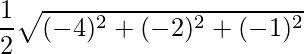
=> Area = 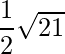
=> Area = √21/2
Question 31. The two adjacent sides of a parallelogram are 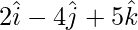 and
and 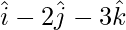 . Find the unit vector parallel to one of its diagonals. Also, find its area.
. Find the unit vector parallel to one of its diagonals. Also, find its area.
Solution:
Given a parallelogram ABCD and its 2 sides AB and BC.
By triangle law of addition,
=> 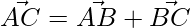
=> 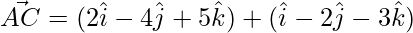
=> ![Rendered by QuickLaTeX.com \vec{AC} = \hat{i}[2+1] +\hat{j}[-4-2]+\hat{k}[5-3]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d793c2d26ee161e09e41d80cdbf6220_l3.png)
=> 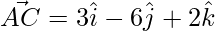
Unit vector is,
=> 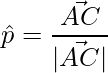
=> 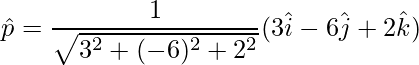
=> 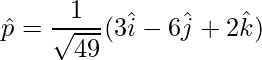
=> 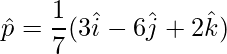
Area of a parallelogram whose adjacent sides are given is 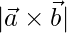
=> 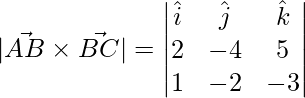
=> ![Rendered by QuickLaTeX.com |\vec{AB}\times\vec{BC}| = \hat{i}[12+10]-\hat{j}[-6-5]+\hat{k}[-4+4]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-918a1d5ec82a7690b20a6ddca73401b5_l3.png)
=> 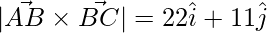
Thus area is,
=> Area = 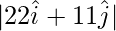
=> Area = 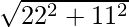
=> Area = 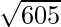
=> Area = 11 √5 square units
Question 32. If either 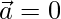 or
or 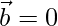 , then
, then 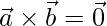 . Is the converse true? Justify with example.
. Is the converse true? Justify with example.
Solution:
Let us take two parallel non-zero vectors  and
and 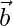
=> 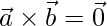
For example,
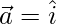 and
and 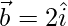
=> 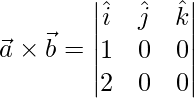
=>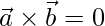
But,
=> 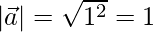
=> 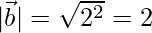
Hence the converse may not be true.
Question 33. If 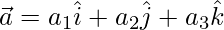 ,
, 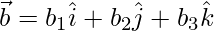 and
and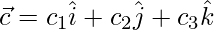 , then verify that
, then verify that 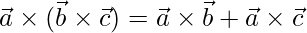 .
.
Solution:
Given, 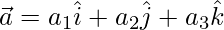 ,
, 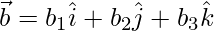 and
and 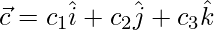
=>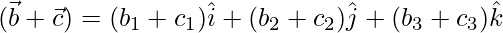
=> 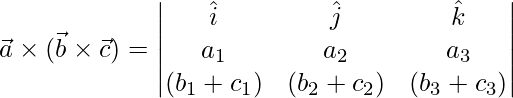
=> ![Rendered by QuickLaTeX.com \vec{a}\times(\vec{b}\times\vec{c}) = \hat{i}[a_2(b_3+c_3)-a_3(b_2+c_2)]-\hat{j}[a_1(b_3+c_3)-a_3(b_1+c_1)]+\hat{k}[a_1(b_2+c_2)-a_2(b_1+c_1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e6575ff3ed0bc464d72b6f539b305a0d_l3.png)
=> ![Rendered by QuickLaTeX.com \vec{a}\times(\vec{b}\times\vec{c}) = \hat{i}[a_2b_3+a_2c_3-a_3b_2-a_3c_2]+\hat{j}[-a_1b_3-a_1c_3+a_3b_1+a_3c_1]+\hat{k}[a_1b_2+a_1c_2-a_2b_1-a_2c_1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dacf3c598173ab16afe142aa6a96c472_l3.png) …..eq(1)
…..eq(1)
Now,
=> 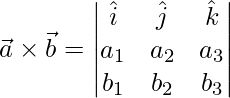
=> ![Rendered by QuickLaTeX.com \vec{a}\times\vec{b} = \hat{i}[a_2b_3-b_2a_3]-\hat{j}[a_1b_3-b_1a_3]+\hat{k}[a_1b_2-b_1a_2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc83e7d5884d3dc7a3ca983b3ead0627_l3.png)
And,
=> 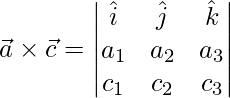
=>![Rendered by QuickLaTeX.com \vec{a}\times\vec{c} = \hat{i}[a_2b_3-c_2a_3]-\hat{j}[a_1c_3-c_1a_3]+\hat{k}[a_1c_2-c_1a_2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aeb7d86907d66ff3a1764c2cdd25ddea_l3.png)
Thus,
=> ![Rendered by QuickLaTeX.com \vec{a}\times\vec{b}+\vec{a}\times\vec{c} = (\hat{i}[a_2b_3-b_2a_3]-\hat{j}[a_1b_3-b_1a_3]+\hat{k}[a_1b_2-b_1a_2]) + (\hat{i}[a_2b_3-c_2a_3]-\hat{j}[a_1c_3-c_1a_3]+\hat{k}[a_1c_2-c_1a_2])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7994d23b8520437132356a4731507265_l3.png)
=> ![Rendered by QuickLaTeX.com \vec{a}\times\vec{b}+\vec{a}\times\vec{c} = \hat{i}[a_2b_3+a_2c_3-a_3b_2-a_3c_2]+\hat{j}[-a_1b_3-a_1c_3+a_3b_1+a_3c_1]+\hat{k}[a_1b_2+a_1c_2-a_2b_1-a_2c_1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5d80eae220fe1ecb3f64cd24a250ce99_l3.png) …eq(2)
…eq(2)
Thus eq(1) = eq(2)
Hence proved.
Question 34(i). Using vectors find the area of the triangle with the vertices A(1, 1, 2), B(2, 3, 5), and C(1, 5, 5).
Solution:
Given, A(1, 1, 2), B(2, 3, 5), and C(1, 5, 5)
=> 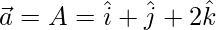
=>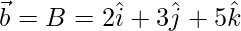
=>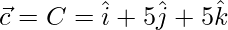
Now 2 sides of the triangle are given by,
=> 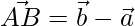
=> 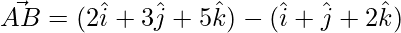
=> ![Rendered by QuickLaTeX.com \vec{AB} = \hat{i}[2-1] +\hat{j}[3-1]+\hat{j}[5-2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a23acbd968b13c7338f8661209200ba7_l3.png)
=> 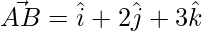
=> 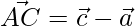
=> 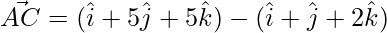
=> ![Rendered by QuickLaTeX.com \vec{AC} = \hat{i}[1-1] +\hat{j}[5-1]+\hat{j}[5-2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-83abe510e6db1c1e54ee6b5f1830e89c_l3.png)
=> 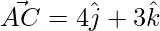
Area of the triangle whose adjacent sides are given is 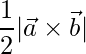
=> 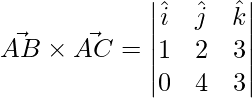
=> ![Rendered by QuickLaTeX.com \vec{AB}\times\vec{AC} = \hat{i}[6-12]-\hat{j}[3-0]+\hat{k}[4-0]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-08e2c2c7868a70bc2ea70b3fd353f02d_l3.png)
=> 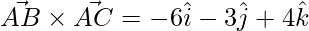
Thus area of the triangle is,
=> Area = 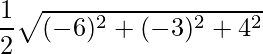
=> Area = 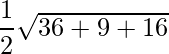
=> Area = √61/2
Question 34(ii). Using vectors find the area of the triangle with the vertices A(1, 2, 3), B(2, -1, 4), and C(4, 5, -1).
Solution:
Given, A(1, 2, 3), B(2, -1, 4), and C(4, 5, -1)
=> 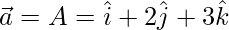
=> 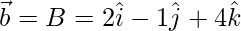
=> 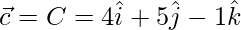
Now 2 sides of the triangle are given by,
=>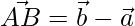
=>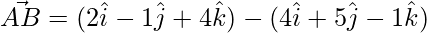
=> ![Rendered by QuickLaTeX.com \vec{AB} = \hat{i}[2-1] +\hat{j}[-1-2]+\hat{j}[4-3]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-19bb8730251934746252a49dd07ac872_l3.png)
=> 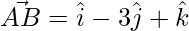
=>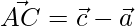
=> 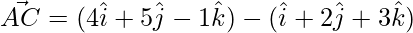
=> ![Rendered by QuickLaTeX.com \vec{AC} = \hat{i}[4-1] +\hat{j}[5-2]+\hat{j}[-1-3]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dc751f0ab79a24e922159d4a8710bceb_l3.png)
=> 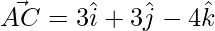
Area of the triangle whose adjacent sides are given is 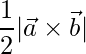
=> 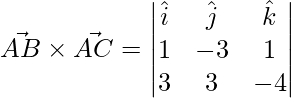
=> ![Rendered by QuickLaTeX.com \vec{AB}\times\vec{AC} = \hat{i}[12-3]-\hat{j}[-4-3]+\hat{k}[3+9]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-39a18f25e02ffeeb73e52a5187333305_l3.png)
=> 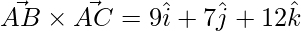
Thus area of the triangle is,
=> Area = 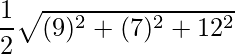
=> Area = 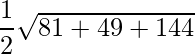
=> Area = √274/2
Question 35. Find all the vectors of magnitude 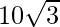 that are perpendicular to the plane of
that are perpendicular to the plane of 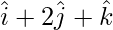 and
and 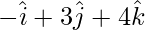 .
.
Solution:
Given, 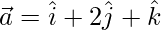 and
and 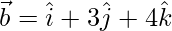
A vector perpendicular to both  and
and 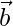 is,
is,
=> 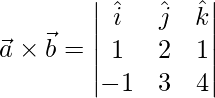
=> ![Rendered by QuickLaTeX.com \vec{a}\times\vec{b} = \hat{i}[8-3]-\hat{j}[4+1]+\hat{k}[3+2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5105a071eb73ce1404c12f2ab06b7190_l3.png)
=> 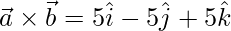
Unit vector is,
=> 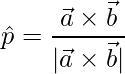
=>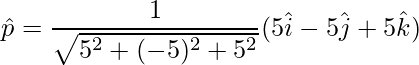
=> 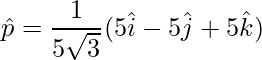
=> 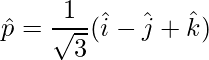
Now vectors of magnitude 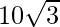 are given by,
are given by,
=> 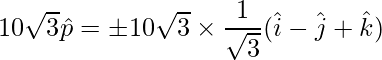
=> Required vectors, 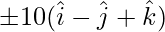
Question 36. The adjacent sides of a parallelogram are 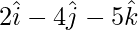 and
and 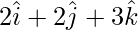 . Find the 2 unit vectors parallel to its diagonals. Also, find its area of the parallelogram.
. Find the 2 unit vectors parallel to its diagonals. Also, find its area of the parallelogram.
Solution:
Given, 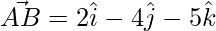 and
and 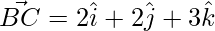
=> 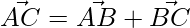
=>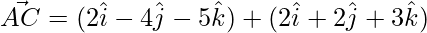
=> 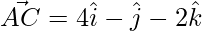
Unit vector is,
=> 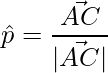
=> 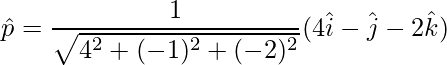
=> 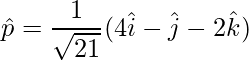
Area is given by 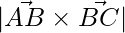 ,
,
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...