Class 12 RD Sharma Solutions – Chapter 25 Vector or Cross Product – Exercise 25.1 | Set 2
Last Updated :
28 Mar, 2021
Question 13. If 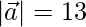 ,
, 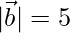 and
and 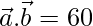 , find
, find 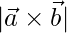
Solution:
We know that,
=> 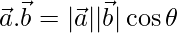
=>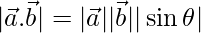
=> 
=> 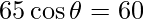
=>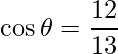
Also,
=>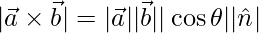
And 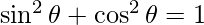
=> 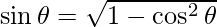
=> 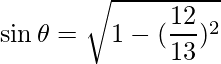
=> 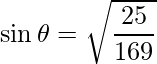
=> 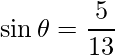
=> 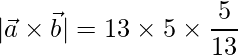
=>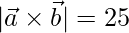
Question 14. Find the angle between 2 vectors 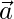 and
and 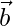 , if
, if 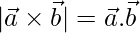
Solution:
Given 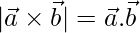
=>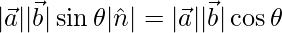
=>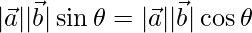 , as
, as 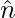 is a unit vector.
is a unit vector.
=> 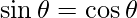
=> 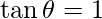
=> 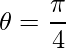
Question 15. If 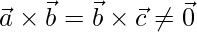 , then show that
, then show that 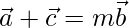 , where m is any scalar.
, where m is any scalar.
Solution:
Given that 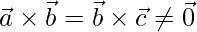
=> 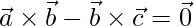
=> ![Rendered by QuickLaTeX.com \vec{a}\times\vec{b} -[-(\vec{c}\times\vec{a})] = \vec{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-248cba952e72a548dc0f5d4bc45d3f09_l3.png)
=>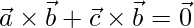
Using distributive property,
=> 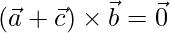
If two vectors are parallel, then their cross-product is 0 vector.
=> 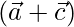 and
and 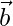 are parallel vectors.
are parallel vectors.
=> 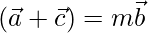
Hence proved.
Question 16. If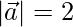 ,
, 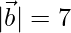 and
and 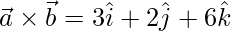 , find the angle between
, find the angle between 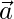 and
and 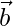
Solution:
Given that,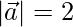 ,
, 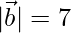 and
and 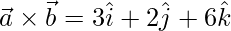
We know that,
=> 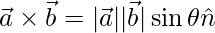
=> 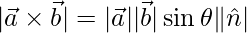
=> 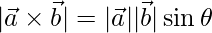
=> 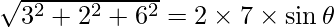
=> 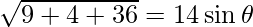
=> 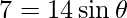
=> 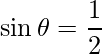
=> 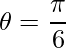
Question 17. What inference can you draw if 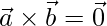 and
and 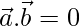
Solution:
Given, 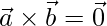 and
and 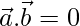
=>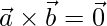
=>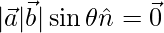
Either of the following conditions is true,
1.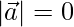
2. 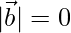
3. 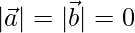
4.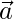 is parallel to
is parallel to 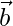
=> 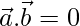
=> 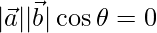
Either of the following conditions is true,
1. 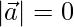
2.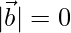
3. 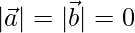
4. 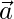 is perpendicular to
is perpendicular to 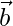
Since both these conditions are true, that implies atleast one of the following conditions is true,
1. 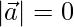
2. 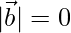
3. 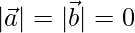
Question 18. If 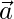 ,
, 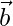 and
and 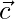 are 3 unit vectors such that
are 3 unit vectors such that 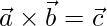 ,
, 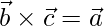 and
and 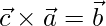 . Show that
. Show that 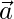 ,
,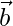 and
and 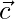 form an orthogonal right handed triad of unit vectors.
form an orthogonal right handed triad of unit vectors.
Solution:
Given, 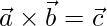 ,
, 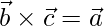 and
and 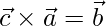
As,
=>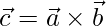
=> 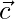 is perpendicular to both
is perpendicular to both 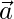 and
and 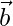 .
.
Similarly,
=> 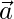 is perpendicular to both
is perpendicular to both 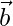 and
and 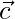
=> 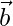 is perpendicular to both
is perpendicular to both 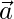 and
and 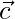
=> 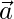 ,
, 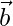 and
and 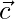 are mutually perpendicular.
are mutually perpendicular.
As, 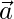 ,
, 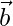 and
and 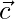 are also unit vectors,
are also unit vectors,
=> 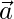 ,
, 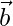 and
and 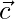 form an orthogonal right-handed triad of unit vectors
form an orthogonal right-handed triad of unit vectors
Hence proved.
Question 19. Find a unit vector perpendicular to the plane ABC, where the coordinates of A, B, and C are A(3, -1, 2), B(1, -1, 3), and C(4, -3, 1).
Solution:
Given A(3, -1, 2), B(1, -1, 3) and C(4, -3, 1).
Let,
=> 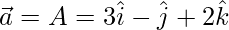
=> 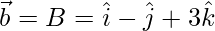
=> 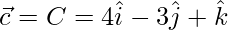
Plane ABC has two vectors 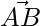 and
and 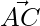
=> 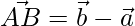
=> 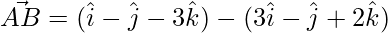
=> 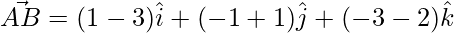
=> 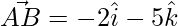
=> 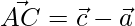
=> 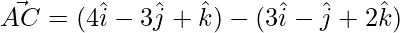
=> 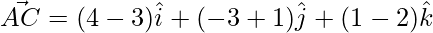
=> 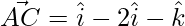
A vector perpendicular to both 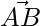 and
and 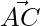 is given by,
is given by,
=> 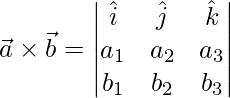
=> 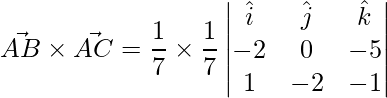
=> ![Rendered by QuickLaTeX.com \vec{AB}\times\vec{AC} = \hat{i}[(0)(-1)-(-2)(-5)] -\hat{j}[(-2)(-1)-(1)(-5)] +\hat{k}[(-2)(-2)-(1)(0)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5ca884f9c9d7761da4ced643aa6267fa_l3.png)
=> ![Rendered by QuickLaTeX.com \vec{AB}\times\vec{AC} = \hat{i}[0-10]-\hat{j}[2+5]+\hat{k}[4-0]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-301ad44b7482ed611d235752a4f1591b_l3.png)
=>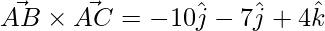
To find the unit vector,
=> 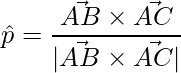
=> 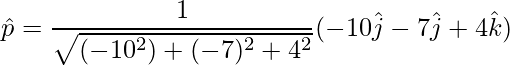
=> 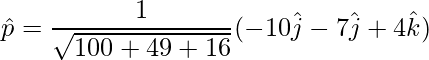
=> 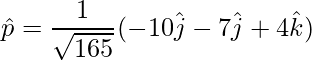
Question 20. If a, b and c are the lengths of sides BC, CA and AB of a triangle ABC, prove that 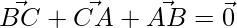 and deduce that
and deduce that 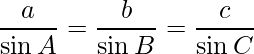
Solution:
Given that 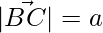 ,
, 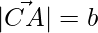 and
and 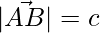
From triangle law of vector addition, we have
=> 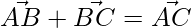
=> 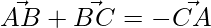
=> 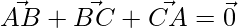
=> 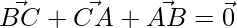
=> 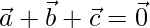
=> 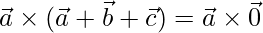
=> 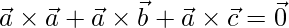
=> 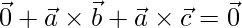
=> 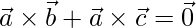
=> 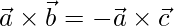
=> 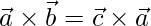
=> 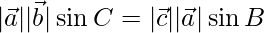
=>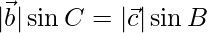
=> 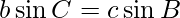
=> 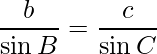
Similarly,
=> 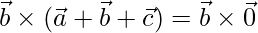
=> 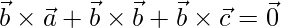
=> 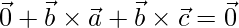
=> 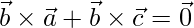
=> 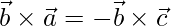
=> 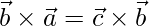
=>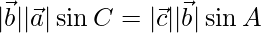
=> 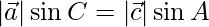
=> 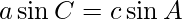
=> 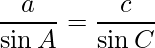
=> 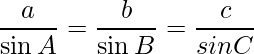
Hence proved.
Question 21. If 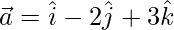 and
and 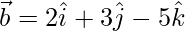 , then find
, then find  . Verify that
. Verify that  and
and  are perpendicular to each other.
are perpendicular to each other.
Solution:
Given, 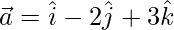 and
and 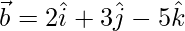
=>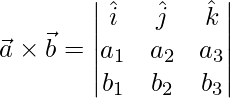
=>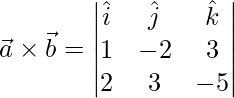
=> ![Rendered by QuickLaTeX.com \vec{a}\times\vec{b} = \hat{i}[(-2)(-5)-(3)(3)]-\hat{j}[(1)(-5)-(2)(3)]+\hat{k}[(1)(3)-(2)(-2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-03a058ff647d59bede2053332811093b_l3.png)
=>![Rendered by QuickLaTeX.com \vec{a}\times\vec{b} = \hat{i}[10-9]-\hat{j}[-5-6]+\hat{k}[3+4]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ebe823d05dd3b8963cbe5c2f8a582228_l3.png)
=> 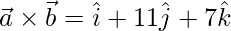
Two vectors are perpendicular if their dot product is zero.
=>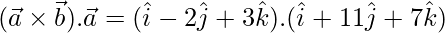
=> 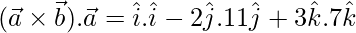
=> 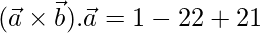
=> 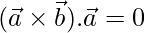
Hence proved.
Question 22. If 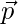 and
and 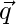 are unit vectors forming an angle of
are unit vectors forming an angle of 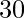 , find the area of the parallelogram having
, find the area of the parallelogram having 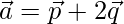 and
and 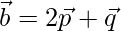 as its diagonals.
as its diagonals.
Solution:
Given 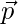 and
and 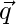 forming an angle of
forming an angle of 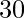 .
.
Area of a parallelogram having diagonals  and
and 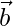 is
is 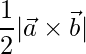
=> 
=> 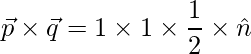
=>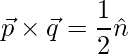
Thus area is,
=> Area = 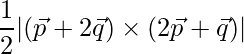
=> Area = 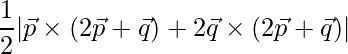
=> Area = 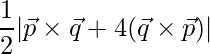
=> Area = 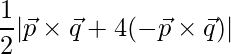
=> Area = 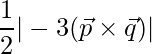
=> Area =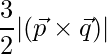
=> Area = 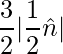
=> Area = 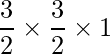
=> Area =  square units
square units
Question 23. For any two vectors  and
and 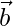 , prove that
, prove that 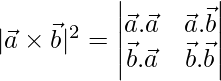
Solution:
We know that,
=> 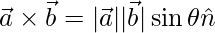
=>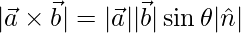
=>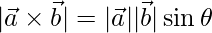
=>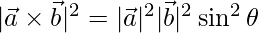
=> 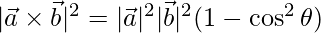
=> 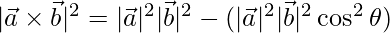
=> 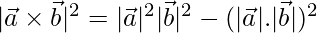
=>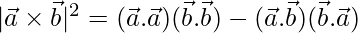
=>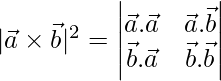
Hence proved.
Question 24. Define  and prove that
and prove that 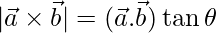 , where
, where 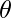 is the angle between
is the angle between  and
and 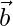
Solution:
Definition of  : Let
: Let  and
and 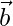 be 2 non-zero, non-parallel vectors. Then
be 2 non-zero, non-parallel vectors. Then  , is defined as a vector with the magnitude of
, is defined as a vector with the magnitude of 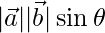 , and which is perpendicular to both the vectors
, and which is perpendicular to both the vectors  and
and 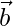 .
.
We know that,
=> 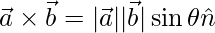
=> 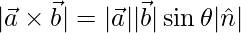
=>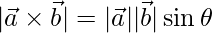 ……………..(eq.1)
……………..(eq.1)
And as,
=> 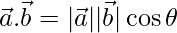
=>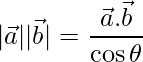
Substituting in (eq.1),
=> 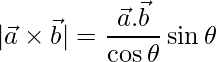
=> 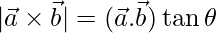
Share your thoughts in the comments
Please Login to comment...