Class 12 RD Sharma Solutions – Chapter 26 Scalar Triple Product – Exercise 26.1
Last Updated :
30 Sep, 2022
Question 1(i). Evaluate the following![Rendered by QuickLaTeX.com [ \hat{i} \hat{j} \hat{k} ] + [ \hat{j} \hat{k} \hat{i} ] + [ \hat{k} \hat{i} \hat{j} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-321bf65c7f550d4316a1b0e6ea13fe7b_l3.png)
Solution:
![Rendered by QuickLaTeX.com [ \hat{i} \hat{j} \hat{k} ] + [ \hat{j} \hat{k} \hat{i} ] + [ \hat{k} \hat{i} \hat{j} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4529ad1945763cf21caa47e6ce18e517_l3.png) =
= 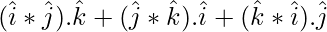
=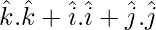
= 1 + 1 + 1
= 3
Question 1(ii). Evaluate the following ![Rendered by QuickLaTeX.com [ 2\hat{i}\ \hat{j}\ \hat{k} ] + [ \hat{i}\ \hat{k}\ \hat{2i} ] + [ \hat{k} \ \hat{j} \ 2\hat{i} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bdc1749ed82dfc078ced4def7bfb1e2e_l3.png)
Solution:
![Rendered by QuickLaTeX.com [ 2\hat{i}\ \hat{j}\ \hat{k} ] + [ \hat{i}\ \hat{k}\ \hat{2i} ] + [ \hat{k} \ \hat{j} \ 2\hat{i} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7affad9f2632e1e3a165c9ee8f2762a2_l3.png) =
= 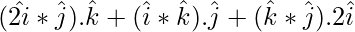
=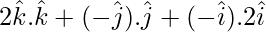
= 2 – 1 – 2
= -1
Question 2(i). Find ![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d3e3ef3aa6d69a1b387296bd8bd1fc6a_l3.png) , when
, when 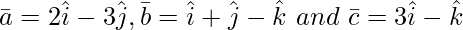
Solution:
![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8dd3c645a45be64c62c8f76dd8bd465f_l3.png) =
= 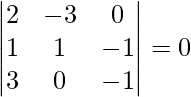
= 2(-1 – 0) + 3(-1 + 3)
= -2 + 6
= 4
Question 2(ii). Find![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8dd3c645a45be64c62c8f76dd8bd465f_l3.png) , when
, when 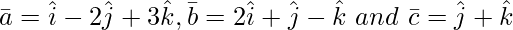
Solution:
![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-204100ba5d1f002ac625831b5ae0a8a4_l3.png) =
= 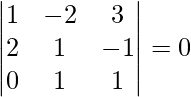
= 1(1 + 1) + 2(2 + 0) + 3(2 – 0)
= 2 + 4 + 6
= 12
Question 3(i). Find the volume of the parallelepiped whose coterminous edges are represented by vector 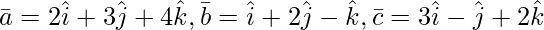
Solution:
Volume of a parallelepiped whose adjacent edges are 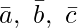 is equal to
is equal to ![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-427c1cfa816a3613e68dfee2651e0c5f_l3.png)
![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) =
= 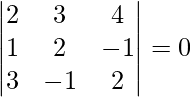
= 2(4 – 1) – 3(2 + 3) + 4(-1 – 6)
= 6 – 15 – 28
= -9 – 28
= -37
So, Volume of parallelepiped is | -37 | = 37 cubic unit.
Question 3(ii). Find the volume of the parallelepiped whose coterminous edges are represented by vector 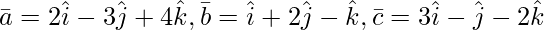
Solution:
Volume of a parallelepiped whose adjacent edges 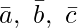 are equal to
are equal to ![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-427c1cfa816a3613e68dfee2651e0c5f_l3.png)
![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-204100ba5d1f002ac625831b5ae0a8a4_l3.png) =
= 
= 2(-4 – 1) + 3(-2 + 3) + 4(-1 – 6)
= -10 + 3 – 28
= -10 – 25
= -35
So, Volume of parallelepiped = | -35 | = 35 cubic unit.
Question 3(iii). Find the volume of the parallelepiped whose coterminous edges are represented by vector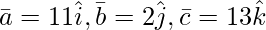
Solution:
Let a = 11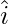 , b = 2
, b = 2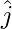 , c = 13
, c = 13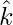
Volume of a parallelepiped whose adjacent edges are 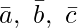 is equal to
is equal to ![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-427c1cfa816a3613e68dfee2651e0c5f_l3.png)
![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) =
= 
= 11(26 – 0) + 0 + 0
= 286
Volume of a parallelepiped = | 286| = 286 cubic units.
Question 3(iv). Find the volume of the parallelepiped whose coterminous edges are represented by vector 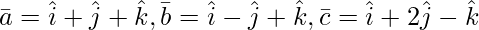
Solution:
Let 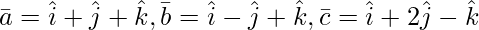
Volume of a parallelepiped whose adjacent edges 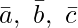 are equal to
are equal to ![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-427c1cfa816a3613e68dfee2651e0c5f_l3.png)
![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) =
=
= 1(1 – 2) – 1(-1 – 1) + 1(2 + 1)
= -1 + 2 + 3
= 4
Volume of a parallelepiped = |4| = 4 cubic units.
Question 4(i). Show of the following triads of vector is coplanar : 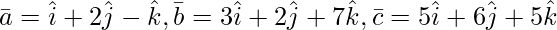
Solution:
As we know that three vectors 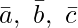 are coplanar if their
are coplanar if their ![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) = 0.
= 0.
![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) =
= 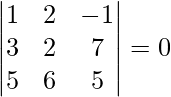
= 1(10 – 42) – 2(15 – 35) – 1(18 – 10)
= -32 + 40 – 8
= 0
So, the given vectors are coplanar.
Question 4(ii). Show of the following triads of vector is coplanar : 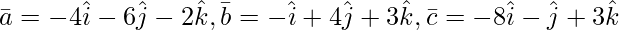
Solution:
As we know that three vectors 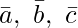 are coplanar if their
are coplanar if their ![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) = 0.
= 0.
![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) =
= 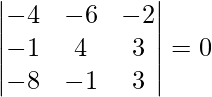
= -4(12 + 3) + 6(-3 + 24) – 2(1 + 32)
= -60 + 126 – 66
= 0
So, the given vectors are coplanar.
Question 4(iii). Show of the following triads of vector is coplanar : 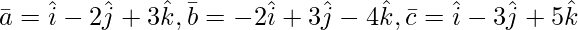
Solution:
As we know that three vectors 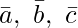 are coplanar if their
are coplanar if their ![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) = 0.
= 0.
![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) =
= 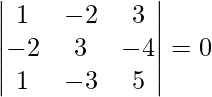
= 1(15 – 12) + 2(-10 + 4) + 3(6 – 3)
= 3 – 12 + 9
= 0
So, the given vectors are coplanar.
Question 5(i). Find the value of λ so that the following vector is coplanar: 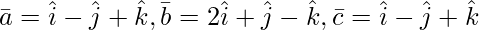
Solution:
As we know that three vectors 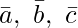 are coplanar if their
are coplanar if their ![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) = 0.
= 0.
![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) =
= 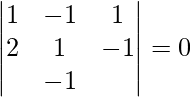
= 1(λ -1) + 1(2λ + λ) + 1(-2 – λ)
= λ – 1 + 3λ – 2 -λ
3 = 3λ
1 = λ
So, the value of λ is 1
Question 5(ii). Find the value of λ so that the following vector is coplanar: 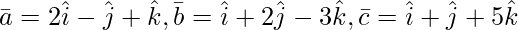
Solution:
As we know that three vectors 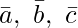 are coplanar if their
are coplanar if their ![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) = 0.
= 0.
![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) =
= 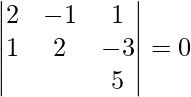
= 2(10 + 3 λ) + 1(5 + 3 λ) + 1(λ – 2 λ)
= 20 + 6 λ + 5 + 3 λ – λ
-25 = 8 λ
λ = – 25 / 8
So, the value of λ is -25/8
Question 5(iii). Find the value of λ so that the following vector is coplanar: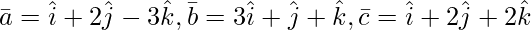
Solution:
Given:
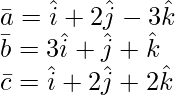
As we know that three vectors 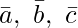 are coplanar if their
are coplanar if their ![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) = 0.
= 0.
![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) =
= 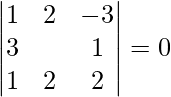
= 1(2λ – 2) – 2(6 – 1) – 3(6 – λ)
= 2λ – 2 -12 + 2 -18 + 3λ
= 5λ – 30
30 = 5λ
λ = 6
So, the value of the λ is 6
Question 5(iv). Find the value of λ so that the following vector is coplanar: 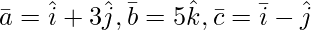
Solution:
Given:
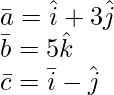
So, to prove that these points are coplanar, we have to prove that ![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) = 0
= 0
![Rendered by QuickLaTeX.com [ \bar{a}\ \bar{b}\ \bar{c} ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-404a9ca0caf96906199210c907b6b5e1_l3.png) =
= 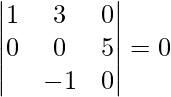
= 1(0 + 5) – 3(0 – 5λ) + 0
= 5 + 15λ
-5 = 15λ
λ = – 1 / 3
Question 6. Show that the four points having position vectors 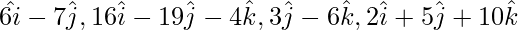 are not coplanar.
are not coplanar.
Solution:
Let us considered
OA = 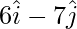
OB = 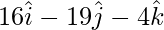
OC = 
OD = 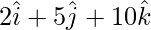
AB = OB – OA = 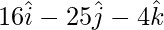
AC = OC – OA = 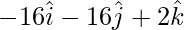
CD = OD – OC = 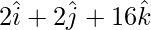
AD = OD – OA = 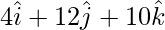
So, to prove that these points are coplanar, we have to prove that ![Rendered by QuickLaTeX.com [\overline{AB} \ \overline{AC} \ \overline{AD} ] =0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2f55526fb37bd7de40dbddb01e446838_l3.png)
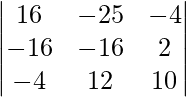
= 16(-160 – 24) + 25(-160 + 8) – 4(-144 + 64) ≠ 0
Hence, proved that the points are not coplanar.
Question 7. Show that the points A (-1, 4, -3), B(3, 2, -5), C(-3, 8, -5), and D(-3, 2, 1) are coplanar
Solution:
Given:
A = (-1, 4, -3)
B = (3, 2, -5)
C = (-3, 8, -5)
D = (-3, 2, 1)
 =
= 
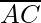 =
= 
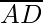 =
= 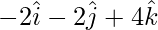
So, to prove that these points are coplanar, we have to prove that ![Rendered by QuickLaTeX.com [\overline{AB} \ \overline{AC} \ \overline{AD}] = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ad58e604a57d129faa663723394654b3_l3.png)
Thus, 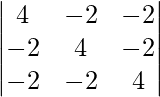
= 4[16 – 4] + 2[-8 -4] – 2[4 + 8]
= 48 – 24 – 24 = 0
Hence, proved.
Question 8. Show that four points whose position vectors are 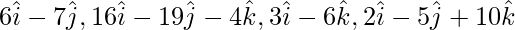
Solution:
Let us considered
OA =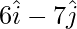
OB = 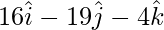
OC = 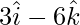
OD =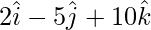
Thus,
AB = OB – OA = 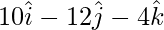
AC = OC – OA = 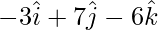
AD = OD – OA = 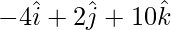
If the vectors AB, AC and AD are coplanar then the four points are coplanar
On simplifying, we get
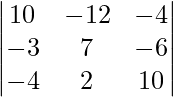
= 10(70 + 12) + 12(-30 – 24) – 4(-6 + 28)
= 820 – 648 – 88
= 84 ≠ 0
So, the points are not coplanar.
Question 9. Find the value of λ for which the four points with position vectors  are coplanar
are coplanar
Solution:
Let us considered:
Position vector of A = 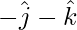
Position vector of B = 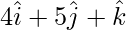
Position vector of C = 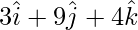
Position vector of D = 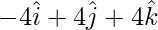
If the given vectors  are coplanar, then the four points are coplanar
are coplanar, then the four points are coplanar
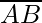 =
= 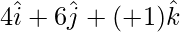
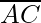 =
= 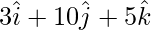
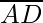 =
= 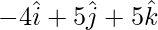
On simplifying, we get
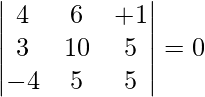
4(50 – 25) – 6(15 + 20) + (λ + 1)(15 + 40) = 0
100 – 210 + 55 + 55λ = 0
55λ = 55
λ = 1
So, when the value of λ = 1, the given points are coplanar.
Question 10. Prove that ![Rendered by QuickLaTeX.com ( \bar{a} - \bar{b} ) . [( \bar{b} - \bar{c} ) * (\bar{ c} - \bar{a} ) ] = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-22e5b3a461e009dffd2d94cffa30b439_l3.png)
Solution:
Given: ![Rendered by QuickLaTeX.com ( \bar{a} - \bar{b} ) . [( \bar{b} - \bar{c} ) * (\bar{ c} - \bar{a} ) ] = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-22e5b3a461e009dffd2d94cffa30b439_l3.png)
One solving the given equation we get
=![Rendered by QuickLaTeX.com [ ( \bar{a} - \bar{b} ) ( \bar{b} - \bar{c} ) ( \bar{c} - \bar{a} ) ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2a1fcce51286054613d2924e8cd2ae19_l3.png)
= ![Rendered by QuickLaTeX.com [ a( \bar{b} - \bar{c} ) ( \bar{c} - \bar{a} ) ] + [ -b ( \bar{b} - \bar{c} ) ( \bar{c} - \bar{a} ) ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d63c17db52dbdbd33466b046eaf3c064_l3.png)
= 6 [ a b c ] – 6 [ a b c ]
= 0
Hence proved
Question 11.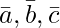 are the position vectors of points A, B and C respectively, prove that
are the position vectors of points A, B and C respectively, prove that  is a vector perpendicular to the plane of triangle ABC.
is a vector perpendicular to the plane of triangle ABC.
Solution:
In the given triangle ABC,
If 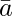 = AB
= AB
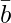 = BC
= BC
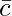 = AC
= AC
Then,
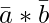 is perpendicular to the plane of the given triangle ABC
is perpendicular to the plane of the given triangle ABC
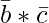 is perpendicular to the plane of the given triangle ABC
is perpendicular to the plane of the given triangle ABC
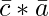 is perpendicular to the plane of the given triangle ABC
is perpendicular to the plane of the given triangle ABC
Hence, proved that 
is a vector perpendicular to the plane of the given triangle ABC.
Question 12(i). Let 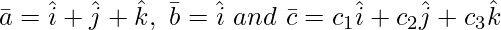 . Then, if c1 = 1 and c2 = 2, find c3 which makes
. Then, if c1 = 1 and c2 = 2, find c3 which makes 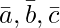 coplanar.
coplanar.
Solution:
Given:
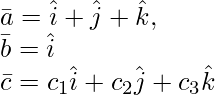
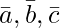 are coplanar only if
are coplanar only if ![Rendered by QuickLaTeX.com [\bar{a}, \bar{b}, \bar{c}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b4b8f2e04409d50020d81298b4215db5_l3.png) = 0
= 0
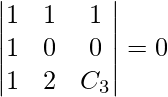
0 – 1(C3) + 1(2) = 0
C3 = 2
So, when the value C3 = 2, then these points are coplanar.
Question 12(ii). Let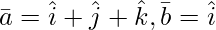 and
and 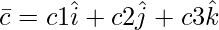 . Then, if c2 = -1 and c3 =1, show that no value of c1 can make
. Then, if c2 = -1 and c3 =1, show that no value of c1 can make 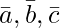 coplanar
coplanar
Solution:
Given:
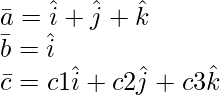
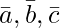 are coplanar only if
are coplanar only if ![Rendered by QuickLaTeX.com [\bar{a}, \bar{b}, \bar{c}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0c875c0fa56b9384070a2f4961cc63b7_l3.png) = 0
= 0
So,
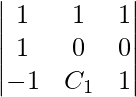
0 – 1 + 1 (C1) = 0
C1 = 1
Hence, prove that no value of C1 can make these points coplanar
Question 13. Find λ for which the points A (3, 2, 1), B (4, λ, 5), C (4, 2, -2), and D (6, 5, -1) are coplanar
Solution:
Let us considered:
Position vector of OA = 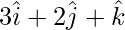
Position vector of OB = 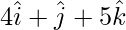
Position vector of OC = 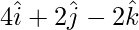
Position vector of OD = 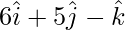
If the vectors AB, AC, and AD are coplanar, then the four points are coplanar
AB =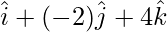
AC =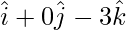
AD = 
On simplifying, we get
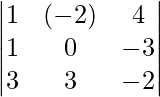
1(9) – (λ – 2)(-2 + 9) + 4(3 – 0) = 0
9 – 7 λ + 14 + 12 = 0
7 λ = 35
λ = 5
Hence, the value of λ is 5. So the coplanar points are, A(3, 2, 1), B(4, 5, 5), C(4, 2, -2), and D(6, 5, -1)
Share your thoughts in the comments
Please Login to comment...