Question 1. Determine whether the following operation define a binary operation on the given set or not:
(i) ‘*’ on N defined by a * b = ab for all a, b ∈ N.
(ii) ‘O’ on Z defined by a O b = ab for all a, b ∈ Z.
(iii) ‘*’ on N defined by a * b = a + b – 2 for all a, b ∈ N
(iv) ‘×6‘ on S = {1, 2, 3, 4, 5} defined by a × 6 b = Remainder when a b is divided by 6.
(v) ‘+6’ on S = {0, 1, 2, 3, 4, 5} defined by a +6 b
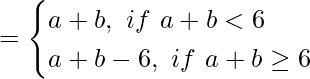
(vi) ‘⊙’ on N defined by a ⊙ b= ab + ba for all a, b ∈ N
(vii) ‘*’ on Q defined by a * b = (a – 1)/ (b + 1) for all a, b ∈ Q
Solution:
(i) Given ‘*’ on N defined by a * b = ab for all a, b ∈ N.
Let a, b ∈ N. Then,
ab ∈ N [∵ ab≠0 and a, b is positive integer]
⇒ a * b ∈ N
Therefore,
a * b ∈ N, ∀ a, b ∈ N
Thus, * is a binary operation on N.
(ii) Given ‘O’ on Z defined by a O b = ab for all a, b ∈ Z.
Both a = 3 and b = -1 belong to Z.
⇒ a * b = 3-1
= 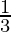 ∉ Z
∉ Z
Thus, * is not a binary operation on Z.
(iii) Given ‘*’ on N defined by a * b = a + b – 2 for all a, b ∈ N
If a = 1 and b = 1,
a * b = a + b – 2
= 1 + 1 – 2
= 0 ∉ N
Thus, there exist a = 1 and b = 1 such that a * b ∉ N
So, * is not a binary operation on N.
(iv) Given ‘×6‘ on S = {1, 2, 3, 4, 5} defined by a ×6 b = Remainder when a b is divided by 6.
Consider the composition table,
| X6 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 4 | 0 | 2 | 4 |
| 3 | 3 | 0 | 3 | 0 | 3 |
| 4 | 4 | 2 | 0 | 4 | 2 |
| 5 | 5 | 4 | 3 | 2 | 1 |
Here all the elements of the table are not in S.
⇒ For a = 2 and b = 3,
a ×6 b = 2 ×6 3 = remainder when 6 divided by 6 = 0 ≠ S
Thus, ×6 is not a binary operation on S.
(v) Given ‘+6’ on S = {0, 1, 2, 3, 4, 5} defined by a +6 b
Consider the composition table,
| +6 | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 | 0 |
| 2 | 2 | 3 | 4 | 5 | 0 | 1 |
| 3 | 3 | 4 | 5 | 0 | 1 | 2 |
| 4 | 4 | 5 | 0 | 1 | 2 | 3 |
| 5 | 5 | 0 | 1 | 2 | 3 | 4 |
Here all the elements of the table are not in S.
⇒ For a = 2 and b = 3,
a ×6 b = 2 ×6 3 = remainder when 6 divided by 6 = 0 ≠ Thus, ×6 is not a binary operation on S.
(vi) Given ‘⊙’ on N defined by a ⊙ b= ab + ba for all a, b ∈ N
Let a, b ∈ N. Then,
ab, ba ∈ N
⇒ ab + ba ∈ N [∵Addition is binary operation on N]
⇒ a ⊙ b ∈ N
Thus, ⊙ is a binary operation on N.
(vii) Given ‘*’ on Q defined by a * b = (a – 1)/ (b + 1) for all a, b ∈ Q
If a = 2 and b = -1 in Q,
a * b = 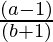
= 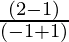
= 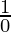 [which is not defined]
[which is not defined]
For a = 2 and b = -1
a * b does not belongs to Q
So, * is not a binary operation in Q.
Question 2. Determine whether or not the definition of * given below gives a binary operation. In the event that * is not a binary operation give justification of this.
(i) On Z+, defined * by a * b = a – b
(ii) On Z+, define * by a*b = ab
(iii) On R, define * by a*b = ab2
(iv) On Z+ define * by a * b = |a − b|
(v) On Z+ define * by a * b = a
(vi) On R, define * by a * b = a + 4b2
Here, Z+ denotes the set of all non-negative integers.
Solution:
(i) Given On Z+, defined * by a * b = a – b
If a = 1 and b = 2 in Z+, then
a * b = a – b
= 1 – 2
= -1 ∉ Z+ [because Z+ is the set of non-negative integers]
For a = 1 and b = 2,
a * b ∉ Z+
Thus, * is not a binary operation on Z+.
(ii) Given Z+, define * by a*b = a b
Let a, b ∈ Z+
⇒ a, b ∈ Z+
⇒ a * b ∈ Z+
Thus, * is a binary operation on R.
(iii) Given on R, define by a*b = ab2
Let a, b ∈ R
⇒ a, b2 ∈ R
⇒ ab2 ∈ R
⇒ a * b ∈ R
Thus, * is a binary operation on R.
(iv) Given on Z+ define * by a * b = |a − b|
Let a, b ∈ Z+
⇒ | a – b | ∈ Z+
⇒ a * b ∈ Z+
Therefore,
a * b ∈ Z+, ∀ a, b ∈ Z+
Thus, * is a binary operation on Z+.
(v) Given on Z+ define * by a * b = a
Let a, b ∈ Z+
⇒ a ∈ Z+
⇒ a * b ∈ Z+
Therefore, a * b ∈ Z+ ∀ a, b ∈ Z+
Thus, * is a binary operation on Z+.
(vi) Given On R, define * by a * b = a + 4b2
Let a, b ∈ R
⇒ a, 4b2 ∈ R
⇒ a + 4b2 ∈ R
⇒ a * b ∈ R
Therefore, a *b ∈ R, ∀ a, b ∈ R
Thus, * is a binary operation on R.
Question 3. Let * be a binary operation on the set I of integers, defined by a * b = 2a + b − 3. Find the value of 3 * 4.
Solution:
Given:
a * b = 2a + b – 3
3 * 4 = 2 (3) + 4 – 3
= 6 + 4 – 3
= 7
Question 4. Is * defined on the set {1, 2, 3, 4, 5} by a * b = LCM of a and b a binary operation? Justify your answer.
Solution:
| LCM | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 2 | 6 | 4 | 10 |
| 3 | 3 | 5 | 3 | 12 | 15 |
| 4 | 4 | 4 | 12 | 4 | 20 |
| 5 | 5 | 10 | 15 | 20 | 5 |
In the given composition table, all the elements are not in the set {1, 2, 3, 4, 5}.
If we consider a = 2 and b = 3, a * b = LCM of a and b = 6 ∉ {1, 2, 3, 4, 5}.
Thus, * is not a binary operation on {1, 2, 3, 4, 5}.
Question 5. Let S = {a, b, c}. Find the total number of binary operations on S.
Solution:
Number of binary operations on a set with n elements is 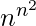
Here, S = {a, b, c}
Number of elements in S = 3
Number of binary operations on a set with 3 elements is 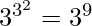
Question 6. Find the total number of binary operations on {a, b}.
Solution:
We have,
S = {a, b}
The total number of binary operation on S = {a, b} in 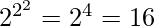
Question 7. Prove that the operation * on the set
M=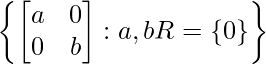 defined by A + B = AB is a binary operation.
defined by A + B = AB is a binary operation.
Solution:
We have,
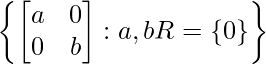 and
and
A + B = AB for all A, B ∈ M
Let A =\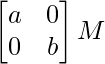 and B =
and B = 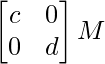
Now, AB = 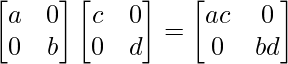
Therefore, a ∈ R, b ∈ R, c ∈ R and d ∈ R
⇒ ac ∈ R and bd ∈ R
⇒ 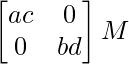
⇒ A * B ∈ M
Hence, the operator * defines a binary operation on M
Question 8. Let S be the set of all rational numbers of the form 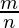 where m ∈ Z and n = 1, 2, 3. Prove that * on S defined by a * b = ab is not a binary operation
where m ∈ Z and n = 1, 2, 3. Prove that * on S defined by a * b = ab is not a binary operation
Solution:
S = set of rational numbers of the form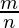 where m ∈ Z and n = 1, 2, 3
where m ∈ Z and n = 1, 2, 3
Also, a * b = ab
Let a ∈ S and b ∈ S
⇒ ab = 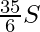
Therefore, a * b ∉ S
Hence, the operator * does not defines a binary operation on S
Question 9. The binary operation & : R × R → R is defined as a*b = 2a + b
Solution:
It is given that, a*b = 2a + b
Now,
(2*3) = 2 × 2 + 3
= 4 + 3
(2*3)*4 = 7*4 = 2 × 7 + 4
= 14 + 4
= 18
Question 10. Let * be a binary operation on N given by a*b = LCM(a, b) for all a, b ∈ N. Find 5*7.
Solution:
It is given that a*b = LCM (a, b)
Now,
5*7 = LCM (5, 7)
= 35
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...