Class 12 RD Sharma Solutions – Chapter 20 Definite Integrals – Exercise 20.1 | Set 1
Last Updated :
02 Jun, 2021
Evaluate the following definite integrals:
Question 1. 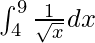
Solution:
We have,
I = 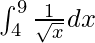
I = ![Rendered by QuickLaTeX.com \left[\frac{x^{\frac{-1}{2}+1}}{\frac{-1}{2}+1}\right]^9_4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-02b35b8e26df515cfadbc6b0f4052d5b_l3.png)
I = ![Rendered by QuickLaTeX.com \left[\frac{x^{\frac{1}{2}}}{\frac{1}{2}}\right]^9_4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b290aa2a3292080c88433221803b31cc_l3.png)
I = ![Rendered by QuickLaTeX.com \left[2\sqrt{x}\right]^9_4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ce12b764d79eaa71ca2f335918febc62_l3.png)
I = 2[√9 – √4 ]
I = 2 (3 − 2)
I = 2 (1)
I = 2
Therefore, the value of 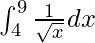 is 2.
is 2.
Question 2. 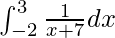
Solution:
We have,
I = 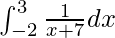
I = ![Rendered by QuickLaTeX.com \left[log(x+7)\right]^3_{-2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ef241fc80fde7ec46dc9370ccdb230ca_l3.png)
I = log (3 + 7) − log (−2 + 7)
I = log 10 − log 5
I = 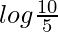
I = log 2
Therefore, the value of 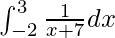 is log 2.
is log 2.
Question 3. 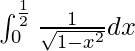
Solution:
We have,
I = 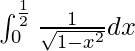
Let x = sin t, so we have,
=> dx = cos t dt
Now, the lower limit is,
=> x = 0
=> sin t = 0
=> t = 0
Also, the upper limit is,
=> x = 1/2
=> sin t = 1/2
=> t = π/6
So, the equation becomes,
I = 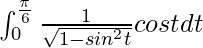
I = 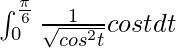
I = 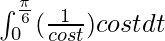
I = 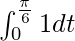
I = ![Rendered by QuickLaTeX.com \left[t\right]_0^{\frac{\pi}{6}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1fcabbbd6391d5c75d8a4dfd82d422dd_l3.png)
I = π/6 – 0
I = π/6
Therefore, the value of 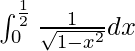 is π/6.
is π/6.
Question 4. 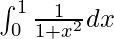
Solution:
We have,
I = 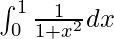
I = ![Rendered by QuickLaTeX.com \left[tan^{-1}x\right]_0^1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d1b68e7b102d6ec00cac374c5a7c28a8_l3.png)
I = 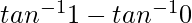
I = 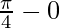
I = π/4
Therefore, the value of 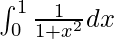 is π/4.
is π/4.
Question 5. 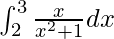
Solution:
We have,
I = 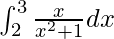
Let x2 + 1 = t, so we have,
=> 2x dx = dt
=> x dx = dt/2
Now, the lower limit is, x = 2
=> t = x2 + 1
=> t = (2)2 + 1
=> t = 4 + 1
=> t = 5
Also, the upper limit is, x = 3
=> t = x2 + 1
=> t = (3)2 + 1
=> t = 9 + 1
=> t = 10
So, the equation becomes,
I = 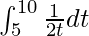
I = 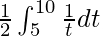
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[logt\right]^{10}_5](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-30da52960c871f4bbfe9b9dc7c477a42_l3.png)
I = 1/2[log10 – log5]
I = 1/2[log10/5]
I = 1/2[log2]
I = log√2
Therefore, the value of 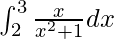 is log√2.
is log√2.
Question 6. 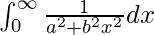
Solution:
We have,
I = 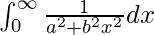
I = 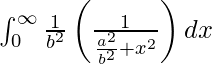
I = 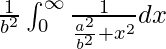
I = ![Rendered by QuickLaTeX.com \frac{1}{b^2}\left[\frac{b}{a}tan^{-1}\frac{bx}{a}\right]^{\infty}_{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f3a4358736d429ea04f0793269f8404c_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{ab}\left[tan^{-1}\frac{bx}{a}\right]^{\infty}_{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9bbe4891bbf69abcc8d2cb41df2ddada_l3.png)
I = 1/ab[tan-1∞ – tan-10]
I = 1/ab[π/2 – 0]
I = 1/ab[π/2]
I = π/2ab
Therefore, the value of 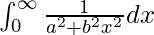 is π/2ab.
is π/2ab.
Question 7. 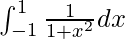
Solution:
We have,
I = 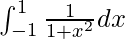
I = ![Rendered by QuickLaTeX.com \left[tan^{-1}x\right]_{-1}^{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7e36928b97b2207cdb45bae25fd98eaf_l3.png)
I = [tan-11 – tan-1(-1)]
I = [π/4 – (-π/4)]
I = [π/4 + π/4]
I = 2π/4
I = π/2
Therefore, the value of 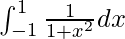 is π/2.
is π/2.
Question 8. 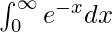
Solution:
We have,
I = 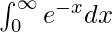
I = ![Rendered by QuickLaTeX.com \left[-e^{-x}\right]^{\infty}_{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a3cc718eacefecd2fbce56168a778a43_l3.png)
I = -e–∞ – (-e0)
I = − 0 + 1
I = 1
Therefore, the value of 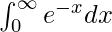 is 1.
is 1.
Question 9. 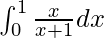
Solution:
We have,
I = 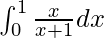
I = 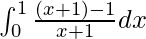
I = 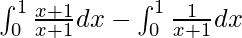
I = 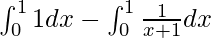
I = ![Rendered by QuickLaTeX.com \left[x\right]^1_0-\left[log(x+1)\right]^1_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1e3cfb2495ed4306090cfa31bb3e7bbd_l3.png)
I = [1 − 0] − [log(1 + 1) − log(0 + 1)]
I = 1 − [log2 − log1]
I = 1 – log2/1
I = 1 − log 2
I = log e − log 2
I = loge/2
Therefore, the value of 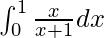 is loge/2.
is loge/2.
Question 10. 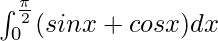
Solution:
We have,
I = 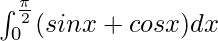
I = 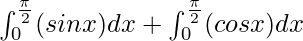
I = ![Rendered by QuickLaTeX.com \left[-cosx\right]_{0}^{\frac{\pi}{2}}+\left[sinx\right]_{0}^{\frac{\pi}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-45a7b48fa2a25a7fefb30e1ce72cd813_l3.png)
I = [-cosπ/2 + cos0] + [sinπ/2 – sin0]
I = [−0 + 1] + 1
I = 1 + 1
I = 2
Therefore, the value of 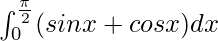 is 2.
is 2.
Question 11. 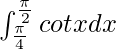
Solution:
We have,
I = 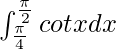
I = ![Rendered by QuickLaTeX.com \left[log(sinx)\right]_{\frac{\pi}{4}}^{\frac{\pi}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3bf8f7a7a5f7aa21f7e6d9d108caeb16_l3.png)
I = log(sinπ/2) – log(sinπ/4)
I = log1 – log1/√2
I = 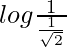
I = log√2
Therefore, the value of 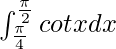 is log√2.
is log√2.
Question 12. 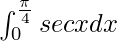
Solution:
We have,
I = 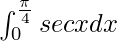
I = ![Rendered by QuickLaTeX.com \left[log(secx+tanx)\right]^{\frac{\pi}{4}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9349195a0cad21481d6a01077a4f6a90_l3.png)
I = log(secπ/4 + tanπ/4 – log(sec0 + tan0)
I = log(√2 + 1) – log(1 + 0)
I = 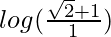
I = log(√2 + 1)
Therefore, the value of 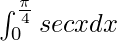 is log(√2 + 1).
is log(√2 + 1).
Question 13. 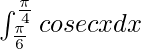
Solution:
We have,
I = 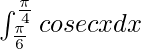
I = ![Rendered by QuickLaTeX.com \left[log|cosecx-cotx|\right]_{\frac{\pi}{6}}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-41a7506890c5a931d9cdc310ad306b66_l3.png)
I = [log|cosecπ/4 – cotπ/4|] – [log|cosecπ/6 – cotπ/6|]
I = [log|√2 – 1|] – [log|2 – √3|]
I = 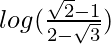
Therefore, the value of 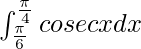 is
is 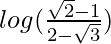 .
.
Question 14. 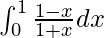
Solution:
We have,
I = 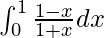
Let x = cos 2t, so we have,
=> dx = –2 sin 2t dt
Now, the lower limit is,
=> x = 0
=> cos 2t = 0
=> 2t = π/2
=> t = π/4
Also, the upper limit is,
=> x = 1
=> cos 2t = 1
=> 2t = 0
=> t = 0
So, the equation becomes,
I = 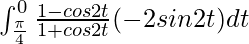
I = 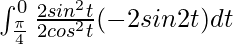
I = 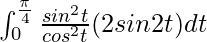
I = 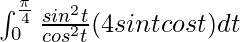
I = 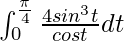
Let cos t = z, so we have,
=> – sin t dt = dz
=> sin t dt = – dz
Now, the lower limit is,
=> t = 0
=> z = cos t
=> z = cos 0
=> z = 1
Also, the upper limit is,
=> t = π/4
=> z = cos t
=> z = cos π/4
=> z = 1/√2
So, the equation becomes,
I = 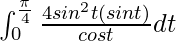
I = 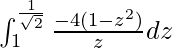
I = 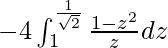
I = 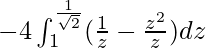
I = 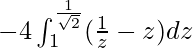
I = ![Rendered by QuickLaTeX.com -4\left[logz-\frac{z^2}{2}\right]^{\frac{1}{\sqrt{2}}}_1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7d85750d6b98e18a00af99aee3d4d8fc_l3.png)
I = -4[(log1/√2 – 1/2(2)) – (log1 – 1/2)]
I = -4[(log1/√2 – 1/4) – (0 – 1/2)]
I = -4[log1/√2 – 1/4 – 0 + 1/2]
I = -4[-log√2 + 1/4]
I = 4log√2 – 1
I = 4 × 1/2log2 – 1
I = 2log2 – 1
Therefore, the value of 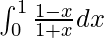 is 2log2 – 1.
is 2log2 – 1.
Question 15. 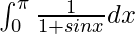
Solution:
We have,
I = 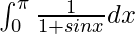
I = 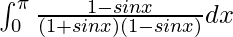
I = 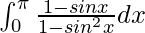
I = 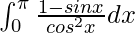
I = 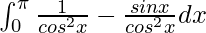
I = 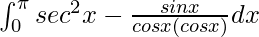
I = 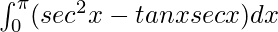
I = 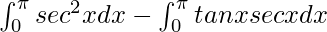
I = ![Rendered by QuickLaTeX.com \left[tanx\right]^{\pi}_0-\left[secx\right]^{\pi}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a10c8701e4a01eac9a86da3846103a0_l3.png)
I = [tan π – tan0] – [sec π – sec 0]
I = [0 – 0] – [–1 – 1]
I = 0 – (–2)
I = 2
Therefore, the value of 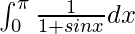 is 2.
is 2.
Question 16. 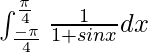
Solution:
We have,
I = 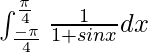
I = 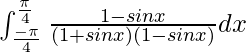
I = 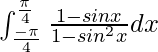
I = 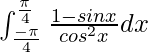
I = 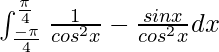
I = 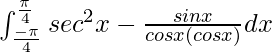
I = 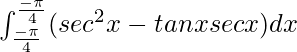
I = 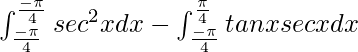
I = ![Rendered by QuickLaTeX.com \left[tanx\right]^{\frac{\pi}{4}}_{\frac{-\pi}{4}}-\left[secx\right]^{\frac{\pi}{4}}_{\frac{-\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0d76195c0a49c58bca6055ab7537bdb2_l3.png)
I = ![Rendered by QuickLaTeX.com \left[tanx\right]^{\frac{\pi}{4}}_{\frac{-\pi}{4}}-\left[secx\right]^{\frac{\pi}{4}}_{\frac{-\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0d76195c0a49c58bca6055ab7537bdb2_l3.png)
I = [tan π/4 – tan(–π/4)] – [sec π/4 – sec (–π/4)]
I = [1 – (–1)] – [sec π/4 – sec (π/4)]
I = 2 – 0
I = 2
Therefore, the value of 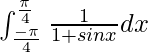 is 2.
is 2.
Question 17. 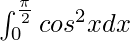
Solution:
We have,
I = 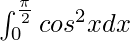
I = 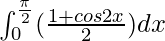
I = 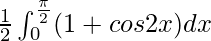
I = 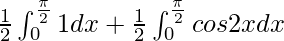
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[x\right]^{\frac{\pi}{2}}_0+\frac{1}{2}\left[\frac{sin2x}{2}\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a0ac14a066022f84853d74bb6c4ea910_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[x\right]^{\frac{\pi}{2}}_0+\frac{1}{4}\left[sin2x\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-309ecf3676d096a63fe4ed039a794d9c_l3.png)
I = 1/2[π/2 – 0] + 1/4[sinπ – sin0]
I = 1/2[π/2] + 1/4[0 – 0]
I = π/4
Therefore, the value of 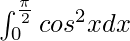 is π/4.
is π/4.
Question 18. 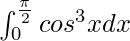
Solution:
We have,
I = 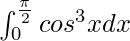
I = 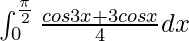
I = 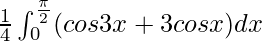
I = 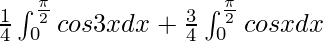
I = ![Rendered by QuickLaTeX.com \frac{1}{4}\left[\frac{sin3x}{3}\right]^{\frac{\pi}{2}}_0+\frac{3}{4}[sinx]^{\frac{\pi}{2}}_{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3fdfea882e0a05b7e73df7fda0aa037b_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{12}\left[sin3x\right]^{\frac{\pi}{2}}_0+\frac{3}{4}[sinx]^{\frac{\pi}{2}}_{0}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b8c64cde5a42a2c4938c81a4c943a6ce_l3.png)
I = 1/12 [-1 – 0] + 3/4[1 – 0]
I = 3/4 – 1/12
I = (9 – 1)/12
I = 8/12
I = 2/3
Therefore, the value of 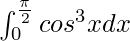 is 2/3.
is 2/3.
Question 19. 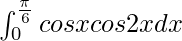
Solution:
We have,
I = 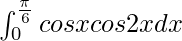
I = 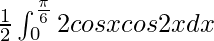
I = 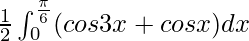
I = 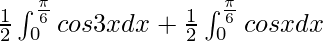
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[\frac{sin3x}{3}\right]^{\frac{\pi}{6}}_0 + \frac{1}{2}\left[sinx\right]^{\frac{\pi}{6}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0ac3bf553d5511e4ffa836e8286f543_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{6}\left[sin3x\right]^{\frac{\pi}{6}}_0 + \frac{1}{2}\left[sinx\right]^{\frac{\pi}{6}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-51fa994cdd67be3c99f696821ef49b43_l3.png)
I = 1/6[sinπ/2 – sin0] + 1/2[sinπ/6 – sin0]
I = 1/6[1 – 0] + 1/2[1/2 – 0]
I = 1/6 + 1/4
I = (4 + 6)/24
I = 10/24
I = 5/12
Therefore, the value of 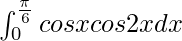 is 5/12.
is 5/12.
Question 20. 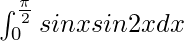
Solution:
We have,
I = 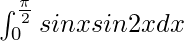
I = 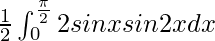
I = 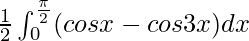
I = 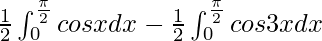
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[sinx\right]^{\frac{\pi}{2}}_0-\frac{1}{2}\left[\frac{sin3x}{3}\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1718138b2e734fce8da23ddf20bcec34_l3.png)
I = ![Rendered by QuickLaTeX.com \frac{1}{2}\left[sinx\right]^{\frac{\pi}{2}}_0-\frac{1}{6}[sin3x]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8a8edce3c8696170eadeb4ab57646ad6_l3.png)
I = 1/2[sinπ/2 – sin0] – 1/6[sin3π/2 – sin0]
I = 1/2[1 – 0] – 1/6[-1 – 0]
I = 1/2 – 1/6(-1)
I = 1/2 + 1/6
I = (6 + 2)/12
I = 8/12
I = 2/3
Therefore, the value of 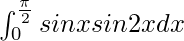 is 2/3.
is 2/3.
Question 21. 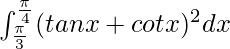
Solution:
We have,
I = 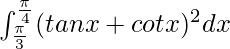
I = 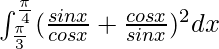
I = 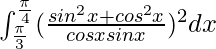
I = 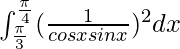
I = 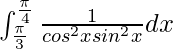
I = 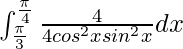
I = 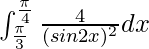
I = 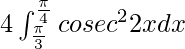
I = ![Rendered by QuickLaTeX.com 4\left[\frac{-cot2x}{2}\right]_{\frac{\pi}{3}}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-75273c4f5e72dbea1096376f56354734_l3.png)
I = ![Rendered by QuickLaTeX.com 2\left[-cot2x\right]_{\frac{\pi}{3}}^{\frac{\pi}{4}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ab97132b5d1a02903279059e7c8e736b_l3.png)
I = 2[-cotπ/2 + cot2π/3]
I = 2[-1/√3 – 0]
I = -2/√3
Therefore, the value of 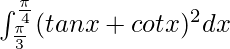 is -2/√3.
is -2/√3.
Question 22. 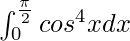
Solution:
We have,
I = 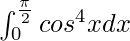
I = 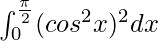
I = 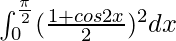
I = 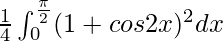
I = 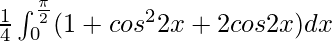
I = 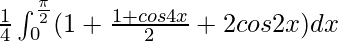
I = ![Rendered by QuickLaTeX.com \frac{1}{4}\left[x+\frac{x}{2}+\frac{sin4x}{8}+sin2x\right]^{\frac{\pi}{2}}_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-40131cf1e496f34031282dd21b7bbbfb_l3.png)
I = 1/4[π/2 + π/4 + 0 + 0 – 0 – 0 – 0 – 0]
I = 1/4[3π/4]
I = 3π/16
Therefore, the value of 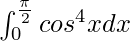 is 3π/16.
is 3π/16.
Share your thoughts in the comments
Please Login to comment...