Question 8. If 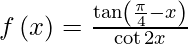 for x ≠ π/4, find the value which can be assigned to f(x) at x = π/4 so that the function f(x) becomes continuous every where in [0, π/2].
for x ≠ π/4, find the value which can be assigned to f(x) at x = π/4 so that the function f(x) becomes continuous every where in [0, π/2].
Solution:
If x ≠ π/4, tan (π/4 – x) and cot2x are continuous in [0, π/2]. Then the function 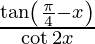 is continuous for each x ≠ π/4.
is continuous for each x ≠ π/4.
Now, let us assume that the point x = π/4.
We have,
(LHL at x = π/4) = lim{x -> π/4-} f(x)
= lim{h -> 0} f(π/4 – h)
= 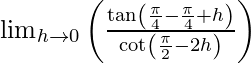
= lim{h -> 0} tan h/tan 2h
= 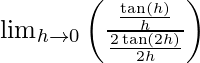
= 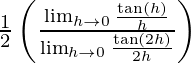
= 1/2
(RHL at x = π/4) = lim{x -> π/4+} f(x)
= lim{h -> 0} f(π/4 + h)
= 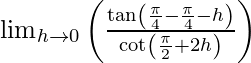
= lim{h -> 0} tan (-h)/tan (-2h)
= lim{h -> 0} tan h/tan 2h
= 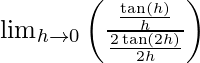
= 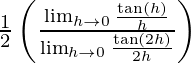
= 1/2
If f(x) is continuous at x = π/4 then
lim{x -> π/4-} f(x) = lim{x -> π/4+} f(x) = f(π/4)
∴ f(π/4) = 1/2
Hence, the function will be everywhere continuous.
Question 9. Discuss the continuity of the function 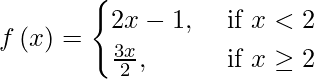 .
.
Solution:
When x < 2, f(x) being a polynomial function is continuous.
When x > 2, f(x) being a polynomial and continuous function is continuous.
At x = 2, we have:
(LHL at x = 2) = lim{x -> 2-} f(x)
= lim{h -> 0} f(2 – h)
= lim{h -> 0} (2(2 – h) – 1)
= 4 – 1
= 3
(RHL at x = 2) = lim{x -> 2+} f(x)
= lim{h -> 0} f(2 + h)
= lim{h -> 0} 3 (h + 2)/2
= 3
Also, f(2) = 3(2)/2 = 3
∴ 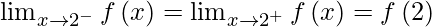
So, f(x) is continuous at x = 2.
Question 10. Discuss the continuity of f(x) = sin |x|.
Solution:
f is clearly the composition of two functions, f = h o g, where g (x) = |x| and h (x) = sin x
Since, hog(x) = h(g(x)) = h(|x|) = \sin|x|
g(x)=|x| being a modulus function must be continuous for all real numbers.
Let us assume that a be a real number.
Case 1:
If a > 0 then g(a) = a
lim{x -> c} (g(x)) = lim{x -> c} (x) = a
So, lim{x -> c} (g(x)) = g(a)
So, g is the continuous on all the points, i.e., x > 0
Case 2:
If a < 0 then g(a) = -a
lim{x -> c} (g(x)) = lim{x -> c} (-x) = -a
So, lim{x -> c} (g(x)) = g(a)
So, g is the continuous on all the points x < 0
Case 3:
If a = 0 then g(a) = g(0) = 0
lim{x -> 0–} (g(x)) = lim{x -> 0–} (-x) = 0
lim{x -> 0+} (g(x)) = lim{x -> 0+} (x) = 0
So, lim{x -> 0–} (g(x)) = lim{x -> 0+}(g(x)) = g(0)
So, g is continues at point x = 0
So, lim{x -> c} (g(x)) = g(a)
So we conclude that h(x) = sinx is defined for every real number.
Let us considered b be the real number. Now put x = b + k
If x->b , then k ->0
So, h(b) = sin b
lim{x -> b} (h(x)) = lim{x -> b} sin x
= lim{k -> 0} sin (b + k)
= lim{k -> 0} (sinb cos k + cos b sink)
= lim{k -> 0} (sinb cos k) + lim{k -> 0}(cos b sink)
= sinb cos 0 + cos b sin 0
= sin b + 0
= sin b
Hence, lim{x -> c} h(x) = g(c)
So, h is continuous function
Hence, f(x) = hog(x) = h(g(x)) = h(|x|) = sin|x|
Question 11. Prove that 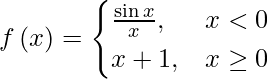 is everywhere continuous.
is everywhere continuous.
Solution:
When x < 0, sin x/x being the composite of two continuous functions is continuous.
When x > 0, we have f(x) being a polynomial function is continuous.
At x = 0:
(LHL at x = 0) = lim{x -> 0–} f(x)
= lim{h -> 0} f(0 – h)
= lim{h -> 0} f(-h)
= lim{h -> 0} (sin (-h)/(-h))
= lim{h -> 0} (sin h/h)
= 1
(RHL at x = 0) = lim{x -> 0+} f(x)
= lim{h -> 0} f(0 + h)
= lim{h -> 0} f(h)
= lim{h -> 0} (h + 1)
= 1
Also, f(x) = 0 + 1 = 1
So we conclude that lim{x -> 0–} f(x) = lim{x -> 0+} f(x) = f(0)
So, f(x) is everywhere continuous.
Question 12. Show that the function g (x) = x − [x] is discontinuous at all integral points. Here [x] denotes the greatest integer function.
Solution:
g is defined at all integral points. Let n be an integer. Then,
g(n) = n − [n]
= n − n
= 0
At x = n, we have:
LHL = lim{x -> n–}g(x) = lim{x->n–}(x – [x])
= lim{x->n–}(x) – lim_{x->n–}[x]
= n − (n − 1)
= 1
RHL = lim{x->n+}g(x) = lim{x->n+} (x – [x])
= lim{x-> n+}(x) – lim{x->n+}[x]
= n − n
= 0
So we conclude that lim{x -> 0–} f( x ) ≠ lim{x -> 0+} f(x)
So, g is discontinuous at all integral points.
Question 13. Discuss the continuity of the following functions:
(i) f(x) = sin x + cos x
(ii) f(x) = sin x − cos x
(iii) f(x) = sin x cos x
Solution:
We know that if g and h are two continuous functions, then g + h, g − h and g o h are also continuous.
Let g (x) = sin x, defined for every real number.
Let a be a real number. Put x = a + h
If x → a, then h → 0 g(a)=sin a.
lim{x->a}g(x) = lim{x->a} sina
= lim{h->0} sin (a+h)
= lim{h->0}[sin a cos h + cos a sin h]
= lim{h->0}(sin a cos h )+lim{h->0}(cos a sin h)
= sin a cos 0 + cos a sin 0
= sin (a + 0)
= sin a
∴ lim{x->c}g(x) = g(c)
Similarly, cos x can be proved as a continuous function.
So we conclude that
(i) f (x) = g (x) + h (x) = sin x + cos x is a continuous function.
(ii) f (x) = g (x) − h (x) = sin x − cos x is a continuous function.
(iii) f (x) = g (x) h (x) = sin x cos x is a continuous function.
Question 14. Show that f (x) = cos x2 is a continuous function.
Solution:
f can be written as the composition of two functions as f = g o h, where g (x) = cos x and h (x) = x2
∵ (g o h)(x) = g(h (x)) = g(x2) = cos(x2) = f(x)
Let c be a real number.
Then, g(c) = cos c
If x-> c , then h->0 and lim{x->c} g(x)
= lim{x->c}cos c
= cos c
∴ lim{x->c}g(x) = g(c)
So, g(x) = cos x is a continuous function.
Now, h(x) = x2
Let k be a real number, then h(k) = k2
limx->h(x) = lim{x->k} x2 = k2
∴ lim{x->k}h(x) = h(k)
So, h is a continuous function.
So, f(x) being a composite of two continuous functions is a continuous function.
Question 15. Show that f (x) = |cos x| is a continuous function.
Solution:
f is the composition of two functions as, f = g o h, where g(x) = |x| and h(x) = cos x
(g o h)(x) = g(h(x)) = g(cos x) = |cos x| = f(x)
Clearly, g(x) being a modulus function would be continuous at all points.
Now, h (x) = cos x. We know that h (x) = cos x is defined for every real number.
Let c be a real number.
Put x = c + h.
If x → c, then h → 0.
⇒ h(c) = cos c
So, h (x) = cos x is a continuous function.
Therefore, f(x) being a composite of two continuous functions is a continuous function.
Question 16. Find all the points of discontinuity of f defined by f (x) = |x| − |x + 1|.
Solution:
f is the composition of two functions as f(x) = g(x) – h(x), where g(x) = |x| and h(x) = |x + 1|.
Let c be a real number.
Case I: If c < 0 , then g(c) = -c and lim{x->c}g(x) = lim{x->c} = -c
∴ lim{x->c}g(x) = g(c)
So, g is continuous at all points x < 0.
Case II: If c < 0 , then g(c) = -c and lim(x->c)g(x) = lim(x->c)(-x) = -c
∴ lim(x->c)g(x) = g(c)
So, g is continuous at all points x > 0.
Case III: if c = 0 , then g (c) = g(0) = 0
lim{x->0-}g(x) = lim{x->0-}(- x) = 0
lim{x->0+}g(x) = lim{x->0+}(x) = 0
∴ lim{x->0+}g(x) = lim{x->0+}(x) = g(0)
So, g is continuous everywhere.
Clearly, h is defined for every real number. Let c be a real number.
Case I: if c < – 1, then h (c) = – (c + 1)
lim{x->c}h (x) = lim{x->c}[-(x + 1)]
= -(c + 1)
∴ lim{x-> c} h (x) = h(c)
Therefore, f being a composite of two continuous functions is a continuous function.
Question 17. Determine if 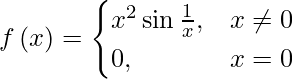 is a continuous function?
is a continuous function?
Solution:
Let us assume that c be a real number.
Case I: If c ≠ 0 , then f(c)= c2 sin (1/c)
lim{x->c}f(x) = lim{x->c}(x2 sin 1/x)
= (lim{x->c}x2) (lim{x->c} sin 1/x)
= c2 sin (1/c)
lim{x->c}f(x) = f(c)
So, f is continuous at all points such that x ≠ 0
Case II: If c = 0 then f(0) = 0
lim{x -> 0–} f(x) = lim{x -> 0–} (x2 sin 1/x) = lim{x -> 0} (x2 sin 1/x)
So, -1 ≤ sin 1/x ≤ 1, x ≠ 0
-x2 ≤ x2sin 1/x ≤ x2
lim{x -> 0} (-x2) ≤ lim{x -> 0} (x2 sin 1/x) ≤ lim{x -> 0} x2
0 ≤ lim{x -> 0} (x2 sin 1/x) ≤ 0
lim{x -> 0} (x2 sin 1/x) = 0
lim{x -> 0–} f(x) = 0
Similarly, lim{x -> 0+} f(x) = lim{x -> 0+} (x2 sin 1/x) = lim{x -> 0} (x2 sin 1/x) = 0
Thus, f is a continuous function.
Question 18. Given the function 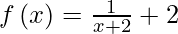 . Find the points of discontinuity of the function f(f(x)).
. Find the points of discontinuity of the function f(f(x)).
Solution:
Here, ![Rendered by QuickLaTeX.com f[f(x)]=\frac{1}{\frac{1}{x+2}+2}=\frac{x+2}{2x+5}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3d6dcc48fd7182e1f6eb056669d187b6_l3.png)
We observe that f(f( x )) is not defined at x + 2 = 0 and 2x + 5 = 0.
If x + 2 = 0, then x = – 2 and if 2x + 5 = 0, then x = -5/2
Hence, the function is discontinuous at x = -5/2 and – 2.
Question 19. Find all point of discontinuity of the function f(t) = 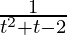 , where t = 1/(x – 1).
, where t = 1/(x – 1).
Solution:
Here, 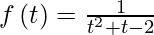
Now, let u = 1/(x – 1)
Therefore f( u ) = 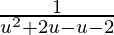
= 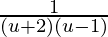
So, f (u ) is not defined at u = -2 and u = 1.
If u = – 2, then -2 = 1/(x – 1)
⇒ 2x = 1
⇒ x = 1/2
If u = 1, then 1 = 1/(x – 1)
⇒ x = 2
Hence, the function is discontinuous at x = 1/2 , 2.
Share your thoughts in the comments
Please Login to comment...