Question 1. Prove that the function 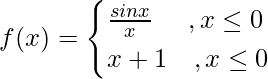 is continuous everywhere.
is continuous everywhere.
Solution:
We know sin x/ x is continuous everywhere since it is the composite function of the functions sin x and x which are continuous.
When x > 0, we have f(x) = x + 1.
Given that 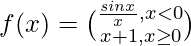
Now, (LHL at x = 0) = lim{x ⇢ 0–} f(x)
= lim{h ⇢ 0} f(0 – h)
= lim{h ⇢ 0} f(-h)
= lim{h ⇢ 0} (sin (-h)/(-h))
= lim{h ⇢ 0} (sin h/ h)
= 1
(RHL at x = 0) = lim{x ⇢ 0+} f(x)
= lim{h ⇢ 0} f(0 + h)
= lim{h ⇢ 0} f(h)
= lim{h ⇢ 0} (h + 1)
= 1
and, f(0) = 0 + 1 = 1.
We observe that: lim{x ⇢ 0–}f(x) = lim{x ⇢ 0+} f(x) = f(0).
Therefore, f(x) is everywhere continuous.
Question 2. Discuss the continuity of the function 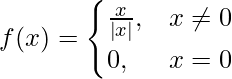 .
.
Solution:
We have,
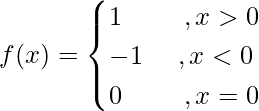
Now: (LHL at x = 0) = lim{x ⇢ 0–} f(x)
= lim{h ⇢ 0} f(0 – h)
= lim{h ⇢ 0} f(–h)
= lim{h⇢ 0} (–1)
= –1
(RHL at x = 0) = lim{x ⇢ 0+} f(x)
= lim{h ⇢ 0} f(0 + h)
= lim{h ⇢ 0} (1)
= 1
We observe that, lim{x ⇢ 0–} f(x) ≠ lim{x ⇢ 0+} f(x).
Therefore, f(x) is discontinuous at x = 0.
Question 3. Find the points of discontinuity, if any, of the following functions:
(i) 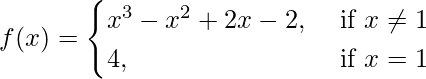
Solution:
Since a polynomial function is everywhere continuous.
At x = 1, we have
(LHL at x = 1) = lim{x ⇢ 1–} f(x)
= lim{h ⇢ 0} f(1 – h)
= lim{h ⇢ 0} ((1 – h)3 – (1 – h )2 + 2(1 – h) – 2)
= 1 – 1 + 2 – 2
= 0
(RHL at x = 1) = lim{x ⇢ 1+} f(x)
= lim{h ⇢ 0} f(1 + h)
= lim{h ⇢ 0} ((1 + h)3 – (1 + h )2 + 2(1 + h) – 2)
= 1 – 1 + 2 – 2
= 0
Also, f(1) = 4.
We observe that, lim{x ⇢ 0–} f(x) = lim{x ⇢ 0+} f(x) ≠ f(1).
Therefore, f(x) is discontinuous only at x = 1.
(ii) 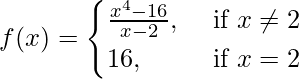
Solution:
When x ≠ 2 then
f(x) = 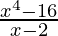
= 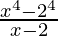
= 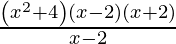
= (x2 + 4)(x + 2)
Since a polynomial function is everywhere continuous, (x2 + 4) and (x + 2) are continuous everywhere.
So, the product function (x2 + 4)(x + 2) is continuous.
Thus, f(x) is continuous at every x ≠ 2 .
We observe that lim{x->2-}f(x) = lim{x->2+}f(x) = f(2)
Therefore, f(x) is discontinuous only at x = 2.
(iii) 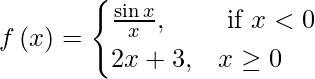
Solution:
When x < 0, then f(x) = sin x/ x.
Since sin x as well as the identity function x are everywhere continuous, the quotient function sin x/x is continuous at each x < 0.
For x > 0, f(x) becomes a polynomial function. Therefore, f(x) is continuous at each x > 0.
We have: (LHL at x = 0) = lim{x->0-}f(x)
= lim{h -> 0} f(0 – h)
= lim{h -> 0} f (-h)
= lim{h -> 0} (sin(-h)/(-h))
= lim{h -> 0} (sin h/h)
= 1
(RHL at x = 0) = lim_{x -> 0+} f(x)
= lim{h -> 0} f(0 + h)
= lim{h -> 0} f(h)
= lim{h -> 0} (2h + 3)
= 3
We observe that lim{x -> 0-} f(x) ≠ lim{x -> 0+} f(x)
Therefore, f(x) is discontinuous only at x = 0.
(iv) 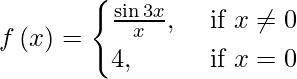
Solution:
At x ≠ 0, then f(x) = sin 3x/ x.
Since the functions sin 3x and x are everywhere continuous. So, the quotient function sin 3x/x is continuous at each x ≠ 0.
We have: (LHL at x = 0) = lim{x -> 0+} f(x)
= lim{h -> 0} f(0 + h)
= lim{h -> 0} f(h)
= lim{h -> 0} (sin 3h/h)
= lim{h -> 0} 3 (sin h/h) = 3
(RHL at x = 0) = lim{x -> 0+} f(x)
= lim{h -> 0} f(0 + h)
= lim{h -> 0} f(h)
= lim{h -> 0} (sin 3h/h)
= lim{h -> 0} 3 (sin 3h/h)
= 3
Also, f(0) = 4.
We observe that lim{x -> 0-} f(x) = lim{x -> 0+} f(x) = f(0)
Therefore, f(x) is discontinuous only at x = 0.
(v) 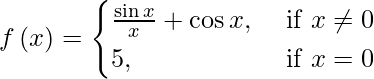
Solution:
When x ≠ 0, then f(x) = sin x/ x + cos x.
We know that sin x as well as cos x are everywhere continuous. Thus, the given function is continuous at each x ≠ 0.
Let us consider the point x = 0.
Given: 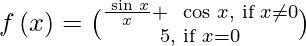
We have: (LHL at x = 0) = lim{x -> 0-} f(x)
= lim{h -> 0} f(0 – h)
= lim{h -> 0} f(-h)
= lim{h -> 0} [(sin (-h)/(-h)) + cos (-h)]
= lim{h -> 0} sin(-h)/(-h) + lim{h -> 0} cos(-h)
= 1 + 1
= 2
(RHL at x = 0) = lim{x -> 0+} f(x)
= lim{h -> 0} f(0 + h)
= lim{h -> 0} f(h)
= lim{h -> 0} [(sin h/h) + cos (-h)]
= lim{h -> 0} sin h/h + lim{h -> 0} cos(-h)
= 1 + 1
= 2
Also, f(0) = 5.
We observe that lim{x -> 0-} f(x) = lim{x -> 0^+} f(x) ≠ f(0)
Therefore, f(x) is discontinuous only at x = 0.
(vi) 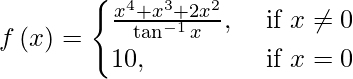
Solution:
When x ≠ 0, then 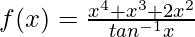
x4 + x3 + 2x2 being a polynomial function is continuous everywhere.
Also, tan-1x is everywhere continuous.
Let us consider the point x = 0.
We have:
(LHL at x = 0) = lim{x -> 0-} f(x)
= lim{h -> 0} f(0 – h)
= lim{h -> 0} f(-h)
= 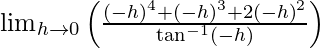
= 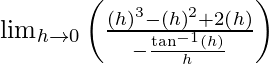
= 0
(RHL at x = 0) = lim{x -> 0+} f(x)
= lim{h -> 0} f(0 + h)
= lim{h -> 0} f(h)
= 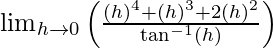
= 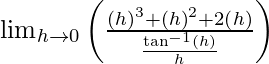
= 0
Also, f(0) = 10.
We observe that lim{x -> 0-} f(x) = lim{x -> 0+} f(x) ≠ f(0)
Therefore, f(x) is discontinuous only at x = 0.
(vii) 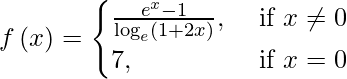
Solution:
We have,
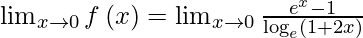
= 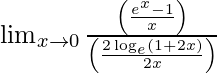
= 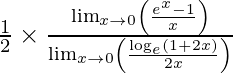
= 1/2
It is given that f(0) = 7.
We observe that lim{x -> 0} f(x) ≠ f(0)
Therefore, f(x) is discontinuous only at x = 0.
(viii) 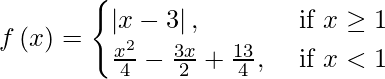
Solution:
At x > 1, f(x) being a modulus function is continuous for each x > 1.
When x < 1, then f( x ) being a composite of polynomial and continuous functions would be continuous.
At x = 1, we have
(LHL at x = 1) = lim{x -> 1-} f(x)
= lim{h -> 0} f(1 – h)
= ![Rendered by QuickLaTeX.com \lim_{h\to0} \left[ \frac{\left( 1 - h \right)^2}{4} - \frac{3\left( 1 - h \right)}{2} + \frac{13}{4} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8cb1facd7269b05ce0c200cab77dbac9_l3.png)
= 1/4 – 3/2 + 13/4
= 2
(RHL at x = 1) = lim{x -> 1+} f(x)
= lim{h -> 0} f(1 + h)
= lim{h -> 0} |1 + h – 3|
= |-2|
= 2
Also f(1) = |1 – 3| = |- 2| = 2
We observe that, lim{x -> 1-} f(x) = lim{x -> 1+} f(x) = f(1)
Therefore, the given function is everywhere continuous.
(ix) 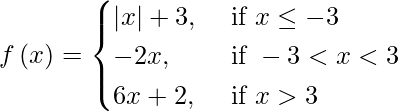
Solution:
f(x) being a modulus function is continuous for each x ≤ – 3.
At – 3 < x < 3 f(x) being a polynomial function is continuous.
At x > 3, f(x) being a polynomial function is continuous.
At x = 3,
We have: (LHL at x = 3) = lim{x -> 3-} f(x)
= lim{h -> 0} f(3 – h)
= lim{h -> 0} -2(3 – h)
= -6
(RHL at x = 3) = lim{x -> 3+} f(x)
= lim{h -> 0} f(3 + h)
= lim{h -> 0} 6(3 + h) + 2
= 20
We observe that lim{x -> 3-} f(x) ≠ lim{x -> 3+} f(x)
Therefore, f(x) is discontinuous only at x = 3.
(x) 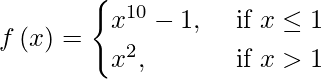
Solution:
According to the question it is given that function f is defined at all the points of the real line.
Let us considered c be a point on the real line.
Case I: If c< 1, then f(c) = c10 −1 and
lim{x-> c} f(x) = lim{x->c} (x10 – 1)
= c10 −1.
∴ lim{x->c} f(x) = f(c)
Hence, f is continuous for all x < 1.
Case II: If c = 1, then the left hand limit of f at x = 1.
The right hand limit of f at x = 1 is, lim(x->1) f(x) = lim(x->1) (x2) = 12 = 1
So we conclude that the left and right hand limit of f at x = 1 do not coincide. So, f is not continuous at x = 1.
Case III: If c>1, then f(c) = c2
lim(x->c) f(x) = lim(x->c) f(c) = c2
∴ lim(x->c) f(x) = f(c)
Therefore, f(x) is discontinuous only at x = 1.
(xi) 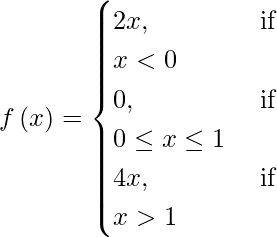
Solution:
Let us considered a be a point on the real line.
Case I: if a < 0, then f(c) = 2a.
lim{x->a}(a) = 2a.
∴ lim{N -> 0}f(x) = f(a)
So, f is continuous at all points such that x < 0.
Case II: If 0 < a < 1 then f(x) and lim{x->a}f(x)=lim{x->a}(0)=0 .
∴ lim{x->a}f(x)=f(a)
So, f is continuous at all points of the interval (0, 1).
Case III: If a =1 then f(a) = f(1) = 0.
The left hand limit of f at x = 1 is,
lim{x->1}f(x) = lim{x->1}f(1)
The right hand limit of f at x = 1 is,
lim{x->1}f(x) = lim{x->1}(4x) = 4(1) = 4
So we conclude that LHL ≠ RHL. Thus, f is not continuous at x = 1.
Case IV: If a > 1, then f(a) = 4a and lim{x->a}f(4x) = 4a .
∴ lim{x->a}f(x) = f(a)
So, f(x) is discontinuous only at x = 1.
(xii) 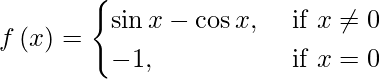
Solution:
It is evident that f is defined at all points of the real line. Let p be a real number.
Case I: if p ≠ 0 , then f (p) = sin p – cos p
lim{x → p}f(x) = lim{x→p}( sin x – cos x ) = sin p – cos p
∴ lim{x →p}f(x) = f(p)
Therefore, f is continuous at all points x, such that x ≠ 0.
Case II: if p = 0 , then f (0) = – 1.
lim{x →0-}f(x) = lim{x →0^-}(sin x – cos x) = sin 0 – cos 0 = 0 – 1 = -1
lim{x →0+}f(x) = lim{x →0}(sin x – cos x) = sin 0 – cos 0 = 0 – 1 = -1
We observe that: lim{x →0-} f (x) = lim{x →0+}f (x)= f(0)
Therefore, f is a continuous function everywhere.
(xiii) 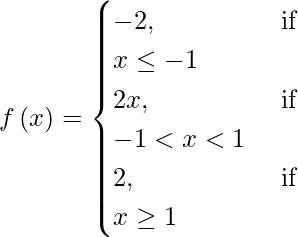
Solution:
The given function is defined at all points of the real line. Let us considered a be a point on the real line.
Case I: If a < -1 then f(a)= -2 and lim{x->a}(x) = lim{x->a}(-2) = -2
∴ lim{x->a}f(x) = f(a)
f is continuous for all x < −1.
Case II: If a =1 then f(a) = f(-1) = -2
LHL = lim{x->-1}f(x) = lim{x->-1}f(-2) = -2
RHL = lim{x->-1}f(x) = lim{x->-1}f(2x) = 2(-1) = -2
We observe that lim{x->-1}f(x) = f(-1)
Therefore, f is continuous at x = −1.
Case III: if -1 < a < 1,then f(a) = 2a
lim{x->a}f(x) = lim{x->a}f(2x) = 2a
∴ lim{x->a}f(x) = f(a)
Therefore, f is continuous at all points of the interval (−1, 1).
Case IV: if a = 1, then f(c) = f(1) = 2(1) = 2.
LHL = lim{x->1}f(x) = lim{x->1}2 = 2
RHL = lim{x->1}f(x) = lim{x->1}2 = 2
We observe that: lim{x->1}f(x) = lim{x->1}f(c)
Therefore, f is continuous at x = 2.
Therefore, f is a continuous function everywhere.
Question 4. In the following, determine the value of constant involved in the definition so that the given function is continuous:
(i) 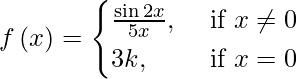
Solution:
If f( x ) is continuous at x = 0, then
⇒ lim{x -> 0} f(x) = f(0)
⇒ lim{x -> 0} sin 2x/5x = f(0)
⇒ lim{x -> 0} 2 sin 2x/10x = f(0)
⇒ 2/5 lim{x -> 0} sin 2x/2x = f(0)
⇒ k = 2/15
(ii) 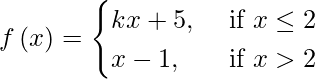
Solution:
If f(x) is continuous at x = 2, then
lim{x -> 2-} f(x) = lim{x -> 2+} f(x)
⇒ lim{h -> 0} (k (2 – h) + 5) = lim{h -> 0} (2 + h -1)
⇒ lim{h -> 0} f(2 – h) = lim{h -> 0} f(2 + h)
⇒ 2k + 5 = 1
⇒ 2k = – 4
⇒ k = – 2
(iii) 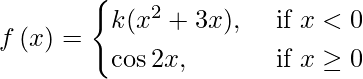
Solution:
If f(x) is continuous at x = 0, then
lim{x -> 0-} f(x) = lim{x -> 0+} f(x)
⇒ lim{h -> 0} f(-h) = lim{h -> 0} f(h)
⇒ 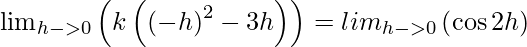
⇒ 0 = 1, which is not possible
Therefore, the given function is not continuous for any value of k.
(iv) 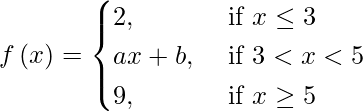
Solution:
If f(x) is continuous at x = 3 and 5, then
lim{x -> 3-} f(x) = lim{x -> 3+} f(x)
and lim{x -> 5-} f(x) = lim{x -> 5+} f(x)
⇒ lim{h -> 0} f(3 – h) = lim{h -> 0} f(3 + h)
and lim{h -> 0} f(5 – h) = lim{h -> 0} f(5 + h)
⇒ 2 = 3a + b and 5a + b = 9
⇒ 2 = 3a + b and 5a + b = 9
⇒ a = 7/2 and b = -17/2.
(v) 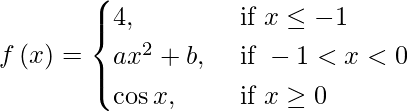
Solution:
If f(x) is continuous at x = −1 and 0, then
lim{x -> -1-} f(x) = lim{x -> – 1+} f(x) and lim{x -> 0-} f(x) = lim{x -> 0+} f(x)
⇒ lim{h -> 0} f(-1 – h) = lim{h -> 0} f(-1 + h) and lim{h -> 0} f(-h) = lim{h -> 0} f(h)
⇒ lim{h -> 0} (4) = lim{h -> 0} (a (-1 + h)2 + b)
Also, 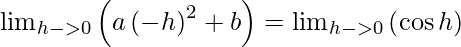
⇒ 4 = a + b and b = 1
⇒ a = 3 and b = 1.
(vi) 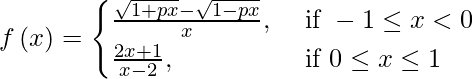
Solution:
If f(x) is continuous at x = 0, then 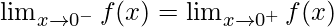
⇒ 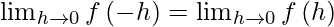
⇒ 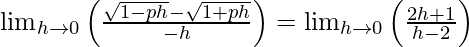
⇒ 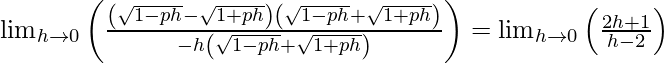
⇒ 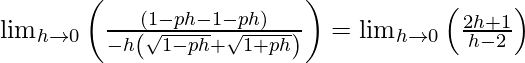
⇒ 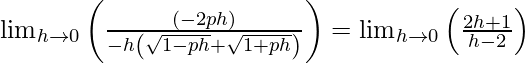
⇒ 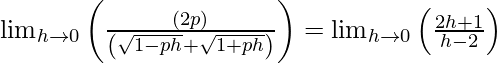
⇒ 2p/2 = -1/2
⇒ p = -1/2.
(vii) 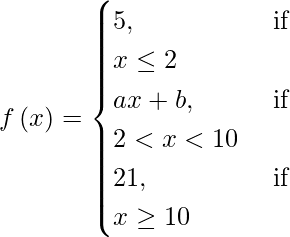
Solution:
If f(x) is continuous at x = 2 and x = 10, then
lim{x -> 2-} f(x) = lim{x -> 2+} f(x) and lim{x -> {10}–} f(x) = lim{x -> {10}+} f(x)
⇒ lim{h -> 0} f(2 – h) = lim{h -> 0} f(2 + h) and lim{h -> 0} f(10 – h) = lim{h -> 0} f(10 + h)
⇒ lim{h -> 0} (5) = lim{h -> 0} (a (2 + h) + b)
And lim{h -> 0} a (10 – h) + b = lim{h -> 0} (21)
On solving equations, we get,
⇒ a = 2 and b = 1.
(viii) 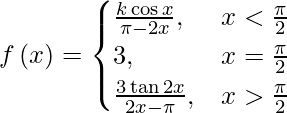
Solution:
If f(x) is continuous at x = π/2, then
lim{x -> π/2-} f(x) = f(π/2)
⇒ lim{h -> 0} f(π/2 – h) = f(π/2)
⇒ lim{h -> 0} f(π/2 – h) = 3
⇒ ![Rendered by QuickLaTeX.com \lim_{h \to 0} \left[ \frac{k \cos \left( \frac{\pi}{2} - h \right)}{\pi - 2\left( \frac{\pi}{2} - h \right)} \right] = 3](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b473429557488541c8a5594f1623c241_l3.png)
⇒ ![Rendered by QuickLaTeX.com \lim_{h \to 0} \left[ \frac{k \sin h}{\pi - \pi + 2h} \right] = 3](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6a74d22a0b8bb9c010069cd835e25a32_l3.png)
⇒ lim{h -> 0} (k sin h/2h) = 3
⇒ k/2 lim{h -> 0} sin h/h =3
⇒ k/2 = 3
⇒ k = 6
Question 5. The function  is continuous on (0, ∞), then find the most suitable values of a and b.
is continuous on (0, ∞), then find the most suitable values of a and b.
Solution:
Given that f is continuous on ( 0, ∞ ).
So, f is continuous at x = 1 and x = √2.
At x = 1, we have lim{x -> 1-} f(x)
= lim{h -> 0} f(1 – h)
= lim{h -> 0} [(1 – h)2/a]
= 1/a
At x = √2, we have
lim{x -> √2-} f(x) = lim{h -> 0} f(√2 + h)
= lim{h -> 0} (a)
= a
![Rendered by QuickLaTeX.com \lim_{x \to \sqrt{2}^+} f\left( x \right) = \lim_{h \to 0} f\left( \sqrt{2} + h \right) = \lim_{h \to 0} \left[ \frac{2 b^2 - 4b}{\left( \sqrt{2} + h \right)^2} \right] = \frac{2 b^2 - 4b}{2} = b^2 - 2b](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a87ad24717e1664aed6493de772b5d24_l3.png)
f is continuous at x = 1 and √2.
⇒ 1/a = a and b2 – 2b = a
⇒ a2 = 1 and b2 – 2b = a
⇒ a = ±1 and b2 – 2b = a . . . (1)
If a = 1, then b2 – 2b = 1
⇒ b2 – 2b – 1 = 0
⇒ b = 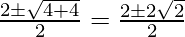 = 1 ± √2
= 1 ± √2
If a = −1, then b2 – 2b = – 1
⇒ b2 – 2b + 1 = 0
⇒ b = 1
Therefore, a = −1, b = 1 or a = 1, b = √2.are the most suitable values of a and b.
Question 6. Find the values of a and b so that the function f(x) defined by 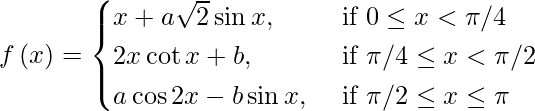 becomes continuous on [0, π].
becomes continuous on [0, π].
Solution:
f is continuous at x = π.
At x = π/4, we have
lim{x -> π/4-} f(x) = lim{h -> 0} f(π/4 – h)
= lim{h -> 0} [(π/4 – h) + √2a sin (π/4 – h)]
= π/4 + √2a sin π/4
= π/4 + a
= lim{h -> 0} [2 (π/4 + h) cot (π/4 + h) + b]
= [2 π/4 cot π/4 + b]
= π/2 + b
⇒ – b – a = b and π/4 + a = π/2 + b
⇒ a = π/6 and b = -π/12
Question 7. The function f(x) is defined as follows: 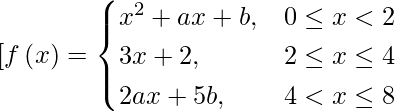 . If f is continuous on [0, 8], find the values of a and b.
. If f is continuous on [0, 8], find the values of a and b.
Solution:
Given that f is continuous on [0, 8].
So, f is continuous at x = 2 and x = 4
At x = 2,
lim{x -> 2-} f(x) = lim{h -> 0} f(2 – h)
= lim{h -> 0} (2 – h)2 + a(2 – h) + b
= 4 + 2a + b
lim{x -> 2+} f(x) = lim{h -> 0} f(2 + h)
= lim{h -> 0} [3(2 + h) + h]
= 8
At x = 4,
lim{x -> 4-} f(x) = lim{h -> 0} f(4 – h)
= lim_{h -> 0} [3(4 – h) + 2]
= 14
lim{x -> 4+} f(x) = lim{h -> 0} f(4 + h)
= lim{h -> 0} [2a(4 + h) + 5b]
= 8a + 5b
So, f is continuous at x = 2 and x = 4.
lim{x -> 2-} f(x) = lim{x -> 2+} f(x)
and, lim{x -> 4-} f(x) = lim{x -> 4+} f(x)
⇒ 4 + 2a + b = 8 and 8a + 5b = 14
⇒ 2a + b = 4 and 8a + 5b = 14
On solving, we get
a = 3 and b = -2
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...