Class 12 NCERT Solutions- Mathematics Part I – Chapter 5 Continuity And Differentiability – Exercise 5.6
Last Updated :
18 Mar, 2021
If x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find 
Question 1. x = 2at2, y = at4
Solution:
Here, x = 2at2, y = at4
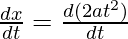
= 2a 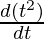
= 2a (2t)
= 4at
And, now
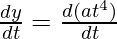
= a 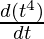
= a (4t3)
= 4at3
Now, as
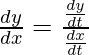
= 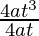
 = t2
= t2
Question 2. x = a cos(θ), y = b cos(θ)
Solution:
Here, x = a cos(θ), y = b cos(θ)
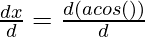
= a 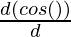
= a (-sin(θ))
= – a sin(θ)
And, now
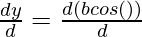
= b 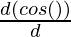
= b (-sin(θ))
= – b sin(θ)
Now, as
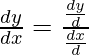
= 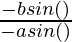
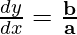
Question 3. x = sin(t), y = cos(2t)
Solution:
Here, x = sin(t), y = cos(2t)
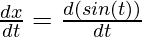
= cos(t)
And, now
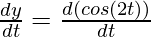
= -sin(2t) 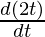
= – 2sin(2t)
Now, as
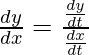
= 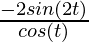
= 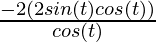 (Using the identity: sin(2θ) = 2 sinθ cosθ)
(Using the identity: sin(2θ) = 2 sinθ cosθ)
 = – 4 sin(t)
= – 4 sin(t)
Question 4. x = 4t, y = 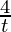
Solution:
Here, x = 4t, y = 4/t
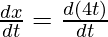
= 4 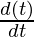
= 4
And, now
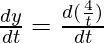
= 4 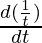
= 4 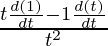
= 4 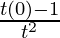
= 4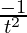
= 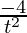
Now, as
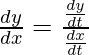
= 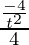
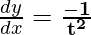
Question 5. x = cos(θ) – cos(2θ), y = sin(θ) – sin(2θ)
Solution:
Here, x = cos(θ) – cos(2θ), y = sin(θ) – sin(2θ)
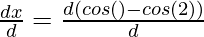
= 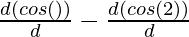
= – sin(θ) – (-sin(2θ)) 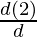
= – sin(θ) + 2sin(2θ)
And, now
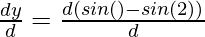
= 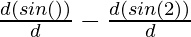
= cos(θ) – (cos(2θ)) 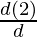
= cos(θ) – (2 cos(2θ)
Now, as
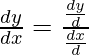
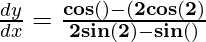
Question 6. x = a (θ – sin(θ)), y = a (1 + cos(θ))
Solution:
Here, x = a (θ – sin(θ)), y = a (1 + cos(θ))
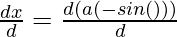
= a (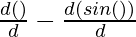 )
)
= a (1 – cos(θ))
And, now
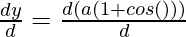
= a (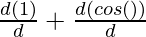 )
)
= a (0 + (- sin (θ)))
= – a sin (θ)
Now, as
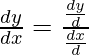
=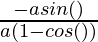
= 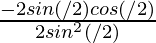 (Using identity: sin(2θ) = 2 sinθ cosθ and 1- cos(2θ) = 2 sin2θ)
(Using identity: sin(2θ) = 2 sinθ cosθ and 1- cos(2θ) = 2 sin2θ)
 = – cot(θ/2)
= – cot(θ/2)
Question 7. x = 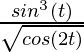 , y =
, y = 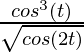
Solution:
Here, x = 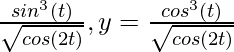
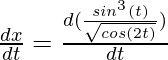
= 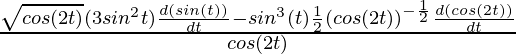
= 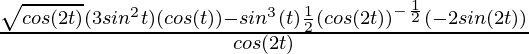
=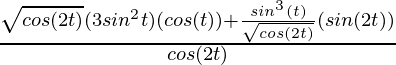
= 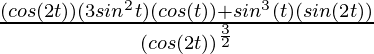
= 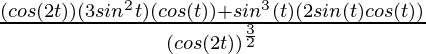
= 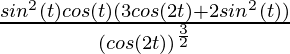
And, now
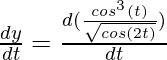
=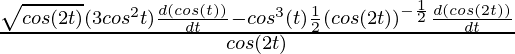
= 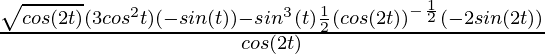
= 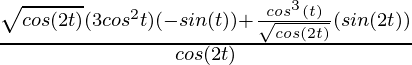
= 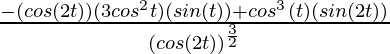
= 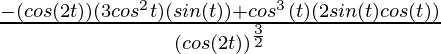
= 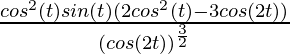
Now, as
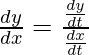
= 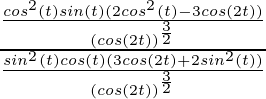
= ![Rendered by QuickLaTeX.com \frac{cos(t) [2cos^2(t) - 3(2 cos^2(t) - 1)]}{sin(t) [3(1 - sin^2(t)) + 2 sin^2(t)]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-295c7057206b40a643349963cbaf953e_l3.png)
= ![Rendered by QuickLaTeX.com \frac{cos(t) [3 - 4 cos^2(t)]}{sin(t) [3 - 4 sin^2(t)]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f41702bb1126338aea529467f1f771f9_l3.png)
= 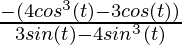
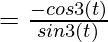
 = – cot 3(t)
= – cot 3(t)
Question 8. x = a (cos(t) + log tan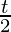 ), y = a sin(t)
), y = a sin(t)
Solution:
Here, x = a (cos(t) + log tan 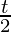 ), y = a sin(t)
), y = a sin(t)
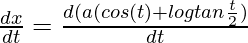
= a (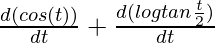 )
)
= a (-sin(t) + 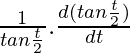 )
)
= a (-sin(t) + 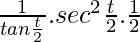 )
)
= a (-sin(t) + 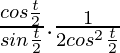 )
)
= a (-sin(t) + 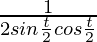 )
)
= a (-sin(t) + 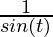 ) (Using identity: 2 sinθ cosθ = sin(2θ))
) (Using identity: 2 sinθ cosθ = sin(2θ))
= a (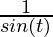 – sin(t))
– sin(t))
= a (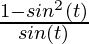 )
)
= a (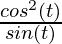 )
)
=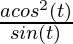
And, now
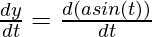
= a 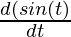
= a cos(t)
Now, as
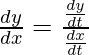
= 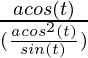
 = tan(t)
= tan(t)
Question 9. x = a sec(θ), y = b tan(θ)
Solution:
Here, x = a sec(θ), y = b tan(θ)
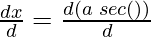
= a (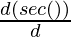 )
)
= a (sec(θ) tan(θ))
= a sec(θ) tan(θ)
And, now
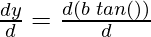
= b (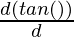 )
)
= b (sec2(θ))
Now, as
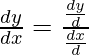
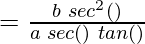
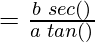
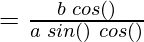
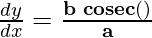
Question 10. x = a (cos(θ) + θ sin(θ)), y = a (sin(θ) – θ cos(θ))
Solution:
Here, x = a (cos(θ) + θ sin(θ)), y = a (sin(θ) – θ cos(θ))
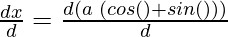
= a (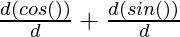 )
)
= a (- sin(θ) + (θ.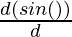 ) + sin(θ).
) + sin(θ).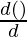 )
)
= a (- sin(θ) + (θ.(cos(θ) + sin(θ).1))
= a (- sin(θ) + θ cos(θ) + sin(θ))
= aθ cos(θ)
And, now
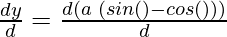
= a (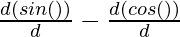 )
)
= a (cos (θ) – (θ.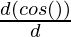 ) + cos(θ).
) + cos(θ).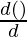 )
)
= a (cos(θ) – (θ.(-sin (θ) + cos(θ).1))
= a (cos(θ) + θ sin(θ) – cos(θ))
= aθ sin(θ)
Now, as
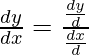
= 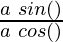
 = tan(θ)
= tan(θ)
Question 11. If x = 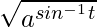 , y =
, y = 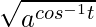 , show that
, show that 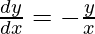
Solution:
Here, Let multiply x and y.
xy = (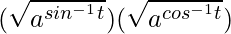 )
)
= (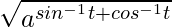 )
)
= (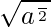 ) (Using identity: sin-1θ + cos-1θ =
) (Using identity: sin-1θ + cos-1θ = 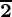 )
)
Let’s differentiate w.r.t x,
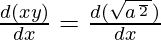
x.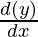 + y.
+ y.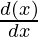 = 0
= 0
x. + y = 0
+ y = 0
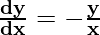
Hence, Proved !!!
Share your thoughts in the comments
Please Login to comment...