Question 31. If 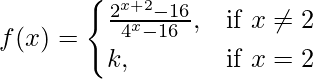 is continuous at x = 2, find k.
is continuous at x = 2, find k.
Solution:
Given that,
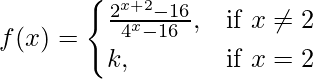
Also, f(x) is continuous at x = 2
So, LHL = RHL = f(2) …..(i)
Now,
f(2) = k ……(ii)
Let us consider LHL,
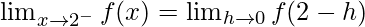
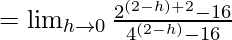
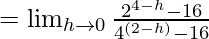
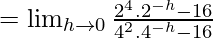
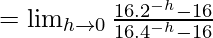
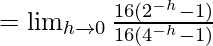
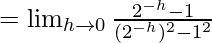
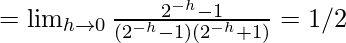 ……(iii)
……(iii)
Using eq(i), (ii) and (iii), we get
k = 1/2
Question 32. If 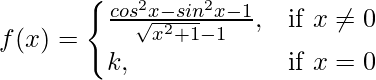 is continuous at x = 0, find k.
is continuous at x = 0, find k.
Solution:
Given that,
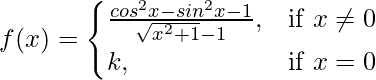
Also, f(x) is continuous at x = 2
So, LHL = RHL
Now,
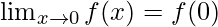
⇒ 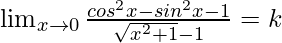
⇒ 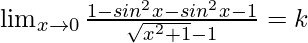
⇒ 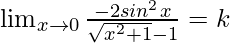
⇒ 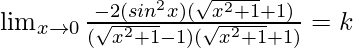
⇒ 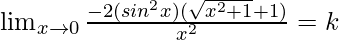
⇒ 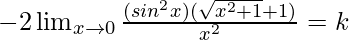
⇒ 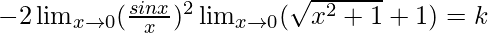
⇒ -2 × 1 × (1 + 1) = k
⇒ k = -4
Question 33. Extend the definition of the following by continuity f(x) = 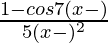 at the point x = π.
at the point x = π.
Solution:
Given that,
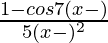
As we know that a f(x) is continuous at x = π if,
LHL = RHL = f(π) ……(i)
Let us consider LHL,
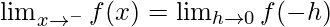
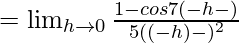
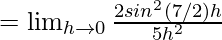
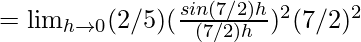
= (2/5) × (49/4) = 49/10
Thus, from eq(i) we get,
f(π) = 49/10
Hence, f(x) is continuous at x = π
Question 34. If f(x) = 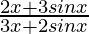 , x ≠ 0 is continuous at x = 0, then find f(0).
, x ≠ 0 is continuous at x = 0, then find f(0).
Solution:
Given that,
f(x) = 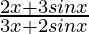
Also, f(x) is continuous at x = 0
So, LHL = RHL = f(0) ……(i)
Let us consider LHL,
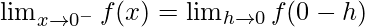
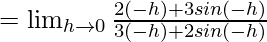
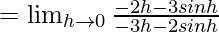
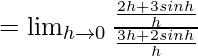
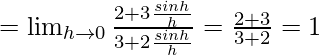
From eq(i) we get,
f(0) = 1
Question 35. Find the value of k for which 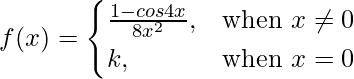 is continuous at x = 0
is continuous at x = 0
Solution:
Given that,
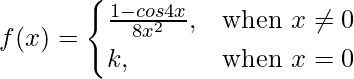
Also, f(x) is continuous at x = 0
LHL = RHL = f(0) …..(i)
f(0) = k
Let us consider LHL,
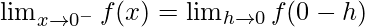
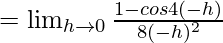
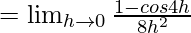
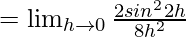
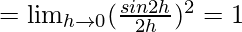
Thus, from eq(i) we get,
k = 1
Question 36. In each of the following, find the value of the constant k so that the given function is continuous at the indicated point:
(i) 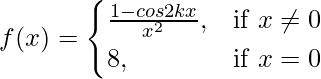 at x = 0
at x = 0
Solution:
Given that,
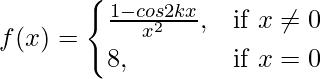
Also, f(x) is continuous at x = 0
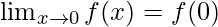
⇒ 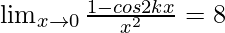
⇒ 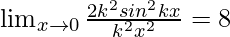
⇒ 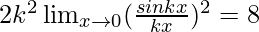
⇒ 2k2 × 1 = 8
⇒ k2 = 4
⇒ k = ±2
(ii) 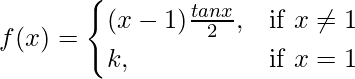 at x = 1
at x = 1
Solution:
Given that,
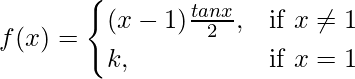
Also, f(x) is continuous at x = 1
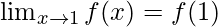
⇒ 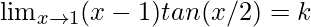
Now, on putting x – 1 = y, we get
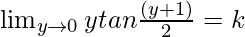
⇒ 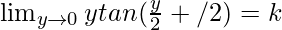
⇒ 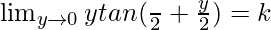
⇒ 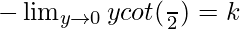
⇒ 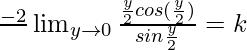
⇒ 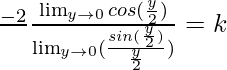
⇒ (-2/π) × (1/1) = k
⇒ k = (-2/π)
(iii) 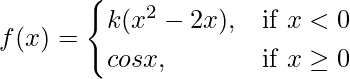 at x = 0
at x = 0
Solution:
Given that,
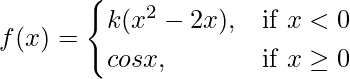
Also, f(x) is continuous at x = 0
Let us consider LHL, at x = 0
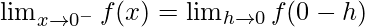
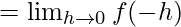
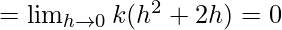
Let us consider RHL at x = 0
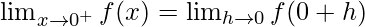
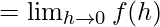
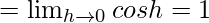
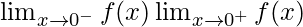
Hence, no value of k exists for which function is continuous at x = 0.
(iv) 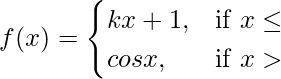 at x = π
at x = π
Solution:
Given that,
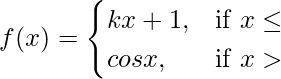
Also, f(x) is continuous at x = π
Let us consider LHL
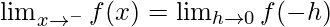
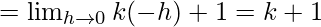
Let us consider RHL
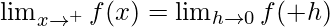
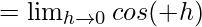
cosπ = -1
As we know that f(x) is continuous at x = π, so
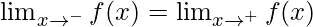
⇒ kπ + 1 = -1
⇒ k = (-2/π)
(v) 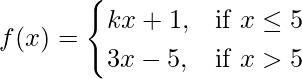 at x = 5
at x = 5
Solution:
Given that,
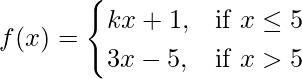
Also, f(x) is continuous at x = 5
Let us consider LHL
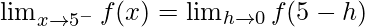
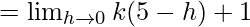
= 5k + 1
Let us consider RHL
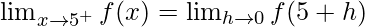
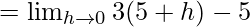
= 10
As we know that f(x) is continuous at x = 5, so
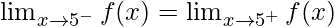
⇒ 5k + 1 = 10
⇒ k = 9/5
(vi) 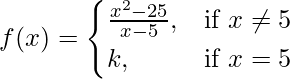 at x = 5
at x = 5
Solution:
Given that,
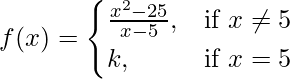
Also, f(x) is continuous at x = 5
So,
f(x) = (x2 – 25)/(x – 5), if x ≠ 5 & f(x) = k, if x = 5
⇒ f(x)= {(x – 5)(x+5)/(x-5)}, if x ≠ 5 & f(x) = k, if x = 5
⇒ f(x)= (x + 5), if x ≠ 5 & f(x) = k, if x = 5
As we know that f(x) is continuous at x = 5, so
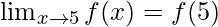
⇒ 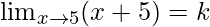
⇒ k = 5 + 5 = 10
(vii) 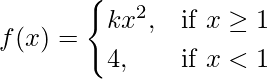 at x = 1
at x = 1
Solution:
Given that,
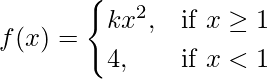
Also, f(x) is continuous at x = 1
Let us consider LHL
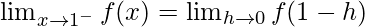
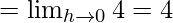
Let us consider RHL
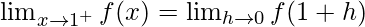
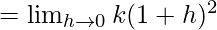
= k
As we know that f(x) is continuous at x = 1, so
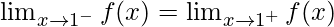
⇒ k = 4
(viii) 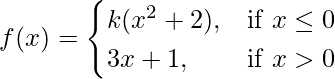 at x = 0
at x = 0
Solution:
Given that,
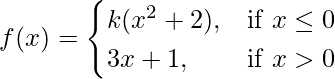
Also, f(x) is continuous at x = 0
Let us consider LHL
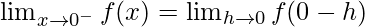
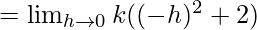
= 2k
Let us consider RHL
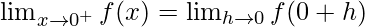
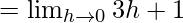
= 1
As we know that f(x) is continuous at x = 0, so
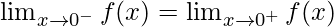
⇒ 2k = 1
⇒ k = 1/2
(ix) 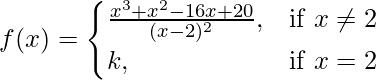 at x = 2
at x = 2
Solution:
Given that,
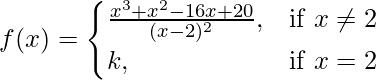
Also, f(x) is continuous at x = 2
f(x)= 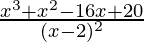 , if x ≠ 2 & f(x) = k, if x = 2
, if x ≠ 2 & f(x) = k, if x = 2
⇒ f(x)= 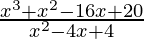 , if x ≠ 2 & f(x) = k, if x = 2
, if x ≠ 2 & f(x) = k, if x = 2
⇒ f(x)= 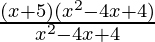 , if x ≠ 2 & f(x) = k, if x = 2
, if x ≠ 2 & f(x) = k, if x = 2
⇒ f(x)= (x + 5), if x ≠ 2 & f(x) = k, if x = 2
As we know that f(x) is continuous at x = 2, so
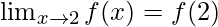
⇒ 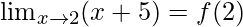
⇒ k = 2 + 5 = 7
Question 37. Find the values of a and b so that the function f given by
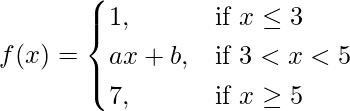 is continuous at x = 3 and x = 5.
is continuous at x = 3 and x = 5.
Solution:
Given that,
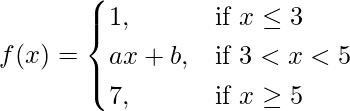
Let us consider LHL at x = 3,
= 1
Let us consider RHL at x = 3,
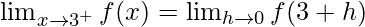
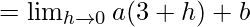
= 3a + b
Let us consider LHL at x = 5,
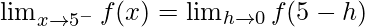
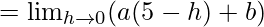
= 5a + b
Let us consider RHL at x = 5,
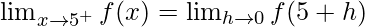
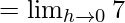
= 7
It is given that f(x) is continuous at x = 3 and x = 5, then
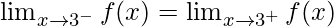 and
and 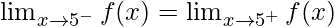
⇒ 1 = 3a + b …..(i)
and 5a + b = 7 …….(ii)
On solving eq(i) and (ii), we get
a = 3 and b = -8
Question 38. If 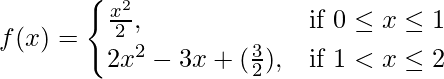 . Show that f is continuous at x = 1.
. Show that f is continuous at x = 1.
Solution:
Given that,
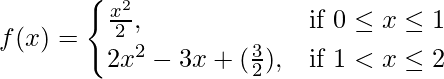
So,
Let us consider LHL at x = 1,
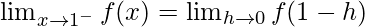
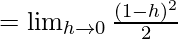
= 1/2
Let us consider RHL at x = 1,
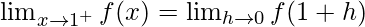
![Rendered by QuickLaTeX.com =\lim_{h\to0}[2(1+h)^2-3(1+h)+3/2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-114c6a8291f2d90b0bfd7d09b82ff15c_l3.png)
= 2 – 3 + 3/2 = 1/2
Also,
f(1) = (1)2/2 = 1/2
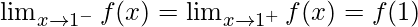
LHL = RHL = f(1)
Hence, the f(x) is continuous at x = 1
Question 39. Discuss the continuity of the f(x) at the indicated points:
(i) f(x) = |x| + |x – 1| at x = 0, 1.
Solution:
Given that,
f(x) = |x| + |x – 1|
So, here we check the continuity of the given f(x) at x = 0,
Let us consider LHL at x = 0,
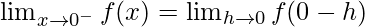
![Rendered by QuickLaTeX.com =\lim_{h\to0}[|0-h|+|0-h-1|]=1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-db43c01835bd0071bc8b033ad5665c26_l3.png)
Let us consider RHL at x = 0,
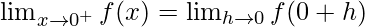
![Rendered by QuickLaTeX.com =\lim_{h\to0}[|0+h|+|0+h-1|]=1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-148f7c3ea7ef59dc454e0329f9222762_l3.png)
Also,
f(0) = |0| + |0 – 1| = 0 + 1 = 1
LHL = RHL = f(0)
Now, we check the continuity of the given f(x) at x = 1,
Let us consider LHL at x = 1,
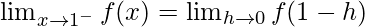
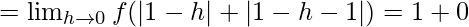
= 1
Let us consider RHL at x = 1
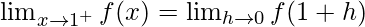
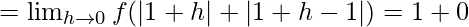
= 1
Also,
f(1) = |1| + |1 – 1| = 1 + 0 = 1
LHL = RHL = f(1)
Hence, f(x) is continuous at x = 0, 1.
(ii) f(x) = |x – 1| + |x + 1| at x = -1, 1.
Solution:
Given that,
f(x) = |x – 1| + |x + 1| at x = -1, 1.
So, here we check the continuity of the given f(x) at x = -1,
Let us consider LHL at x = -1,
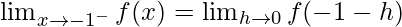
![Rendered by QuickLaTeX.com =\lim_{h\to0}[|-1-h-1|+|-1-h+1|]=2+0=2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b79480bd2b39e2e947ef4577d70999a7_l3.png)
Let us consider RHL at x = -1,
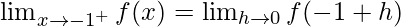
![Rendered by QuickLaTeX.com =\lim_{h\to0}[|-1+h-1|+|-1+h+1|]=2+0=2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9026a8de78b7683c36ff82b727d36910_l3.png)
Also,
f(-1) = |-1 – 1| + |-1 + 1| = |-2| = 2
LHL = RHL = f(-1)
Now, we check the continuity of the given f(x) at x = 1,
Let us consider LHL at x = 1,
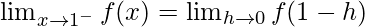
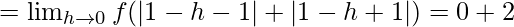
= 2
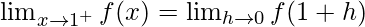
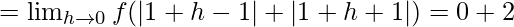
= 2
Also,
f(1) = |1 + 1| + |1 – 1| = 2
LHL = RHL = f(1)
Hence, f(x) is continuous at x = -1, 1.
Question 40. Prove that 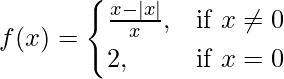 is discontinuous at x = 0.
is discontinuous at x = 0.
Solution:
Prove that 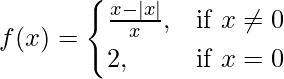 is discontinuous at x = 0.
is discontinuous at x = 0.
Proof:
Let us consider LHL at x = 0,
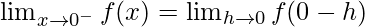
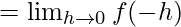
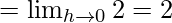
Let us consider RHL at x = 0,
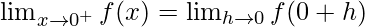
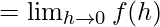
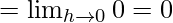
LHL ≠ RHL
Hence, f(x) is discontinuous at x = 0.
Question 41. If 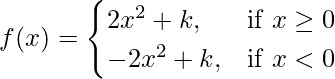 then what should be the value of k so that f(x) is continuous at x = 0.
then what should be the value of k so that f(x) is continuous at x = 0.
Solution:
Given that,
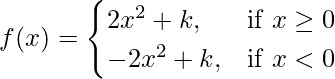
Let us consider LHL at x = 0,
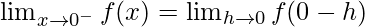
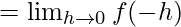
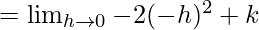
= k
Let us consider RHL at x = 0,
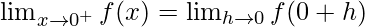
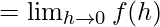
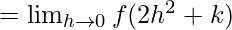
= k
It is given that f(x) is continuous at x = 0.
LHL = RHL = f(0)
⇒ 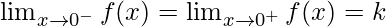
k can be any real number.
Question 42. For what value λ of is the function
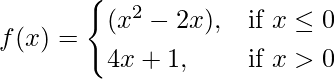 continuous at x = 0 ? What about continuity at x = ±1?
continuous at x = 0 ? What about continuity at x = ±1?
Solution:
Given that,
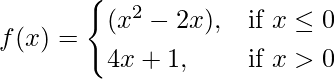
Check for x = 0,
Hence, there is no value of λ for which f(x) is continuous at x = 0.
Now for x = 1,
f(1) = 4x + 1 = 4 × 1 + 1 = 5
Hence, for any values of λ, f is continuous at x = 1.
Now for x = -1,
f(-1) = λ(1 + 2)= 3λ
Hence, for any values of λ, f is continuous at x=-1.
Question 43. For what values of k is the following function continuous at x = 2?
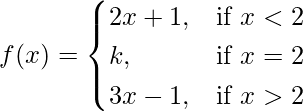
Solution:
Given that,
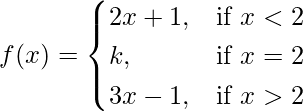
We have,
Let us consider LHL at x = 2,
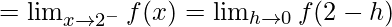
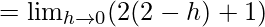
= 5
Let us consider RHL at x = 2,
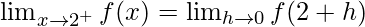
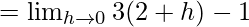
= 5
Also,
f(2) = k
It is given that f(x) is continuous at x = 2.
LHL = RHL = f(2)
⇒ 5 = 5 = k
Hence, for k = 5, f(x) is continuous at x = 2.
Question 44. Let 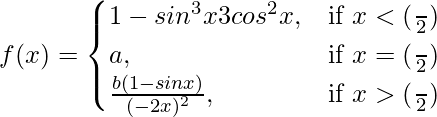 If f(x) is continuous at x = (π/2), find a and b.
If f(x) is continuous at x = (π/2), find a and b.
Solution:
Given that,
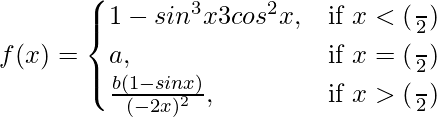
Let us consider LHL at x = π/2
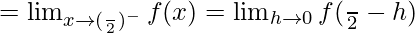
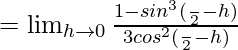
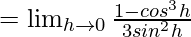
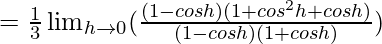
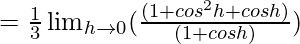
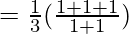
= 1/2
Let us consider RHL at x = π/2
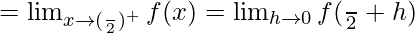
![Rendered by QuickLaTeX.com =\lim_{h\to0}(\frac{b[1-sin(\frac{π}{2}+h)]}{[π-2(\frac{π}{2}+h)]^2})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ae12e394649a5a3c940636de12521e82_l3.png)
![Rendered by QuickLaTeX.com =\lim_{h\to0}(\frac{b(1-cosh)}{[-2h]^2})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f90c115eab1cb0cfeb014b5fdc663190_l3.png)
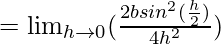
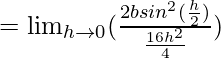
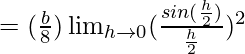
= b/8 × 1
= b/8
Also,
f(π/2) = a
It is given that f(x) is continuous at x = π/2.
LHL = RHL = f(π/2)
So,
⇒ 1/2 = b/8 = a
⇒ a = 1/2 and b = 4
Question 45. If the functions f(x), defined below is continuous at x = 0, find the value of k,
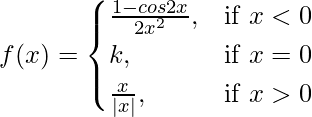
Solution:
Given that,
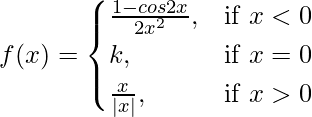
Let us consider LHL at x = 0,
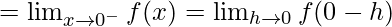
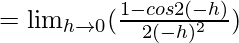
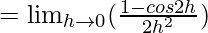
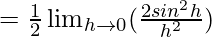
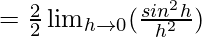
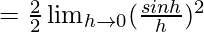
= 1 × 1
Let us consider RHL at x = 0,
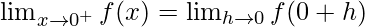
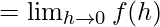
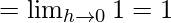
Also,
f(0) = k
It is given that f(x) is continuous at x = 0,
LHL = RHL = f(0)
So,
⇒ 1 = 1 = k
Hence, the required value of k is 1.
Question 46. Find the relationship between ‘a’ and ‘b’ so that function ‘f’ defined by
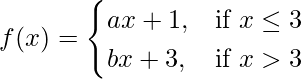 is continuous at x = 3.
is continuous at x = 3.
Solution:
Given that,
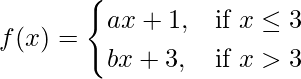
Let us consider LHL at x = 3,
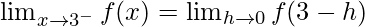
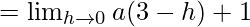
= 3a + 1
Let us consider RHL at x = 3,
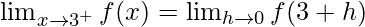
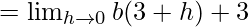
= 3b + 3
It is given that f(x) is continuous at x = 3,
LHL = RHL = f(3)
So,
⇒ 3a + 1 = 3b + 3
⇒ 3a – 3b = 2
Hence, the required relationship between a and b is 3a – 3b = 2.
Share your thoughts in the comments
Please Login to comment...