Class 12 RD Sharma Solutions – Chapter 23 Algebra of Vectors – Exercise 23.9
Last Updated :
28 Mar, 2021
Question 1: Can a vector have direction angles 45°, 60°, and 120°.
Solution:
We know that if l, m and n are the direction cosines and 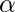 ,
, 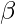 and
and 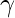 are the direction angles then,
are the direction angles then,
=> 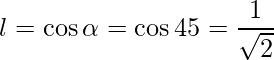
=> 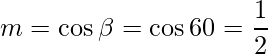
=> 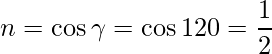
Also,
=> l2 + m2 + n2 = 1
=> 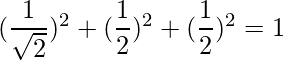
=> 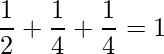
=> As LHS = RHS, the vector can have these direction angles.
Question 2: Prove that 1,1 and 1 can not be the direction cosines of a straight line.
Solution:
Given that, l=1, m=1 and n=1.
We know that,
=> l2 + m2 + n2 = 1
=> 12 + 12 + 12 = 1
=> 3 ≠ 1
Thus, 1, 1 and 1 can never be the direction cosines of a straight line.
=> Hence proved.
Question 3: A vector makes an angle of 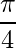 with each of x-axis and y-axis. Find the angle made by it with the z-axis.
with each of x-axis and y-axis. Find the angle made by it with the z-axis.
Solution:
We know that if l, m and n are the direction cosines and 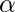 ,
, 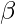 and
and 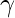 are the direction angles then,
are the direction angles then,
=> 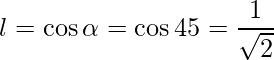
=> 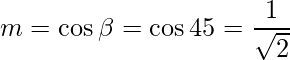
Let 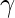 be the angle we have to calculate.
be the angle we have to calculate.
We know that,
=> l2 + m2 + n2 = 1
=> ![Rendered by QuickLaTeX.com n^2 = 1- [(\dfrac{1}{\sqrt{2}})^2+(\dfrac{1}{\sqrt{2}})^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-11b5e5562f22f79b315f5ec4d28cfad1_l3.png)
=> n2 = 1 – 1
=> n2 = 0
=> 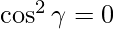
=> 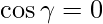
=> 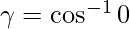
=> 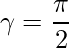
Question 4: A vector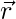 is inclined at equal acute angles to x-axis, y-axis and z-axis. If
is inclined at equal acute angles to x-axis, y-axis and z-axis. If 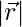 = 6 units, find
= 6 units, find 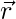 .
.
Solution:
Given that 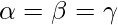
=> 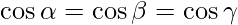
=> l = m = n = p (say)
We know that,
=> l2 + m2 + n2 = 1
=> p2 + p2 + p2 = 1
=> 3p2 = 1
=> 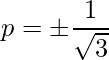
The vector 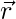 can be described as,
can be described as,
=> 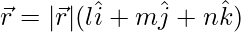
=> 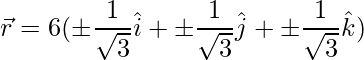
=>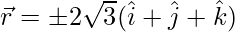
Question 5: A vector 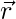 is inclined to the x-axis at 45° and y-axis at 60°. If
is inclined to the x-axis at 45° and y-axis at 60°. If 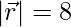 units, find
units, find 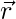 .
.
Solution:
Given that 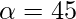 and
and 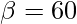
We know that,
=> l2 + m2 + n2 = 1
=> 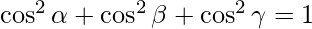
=> 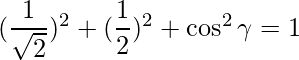
=> ![Rendered by QuickLaTeX.com \cos^2 \gamma = 1- [\dfrac{1}{2}+\dfrac{1}{4}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-681e487ff624c315893ac985c72d6924_l3.png)
=> 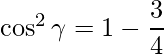
=> 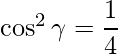
=> 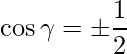
The vector 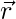 can be described as,
can be described as,
=> 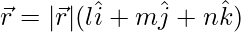
=> 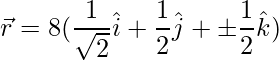
=> 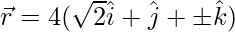
Question 6: Find the direction cosines of the following vectors:
(i): 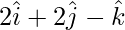
Solution:
The direction ratios are given as 2, 2 and -1.
Direction cosines are given as,
=> 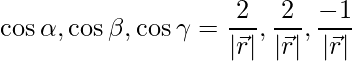
=> 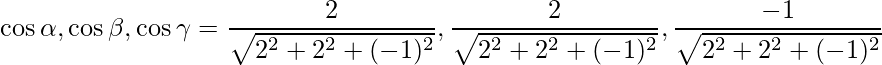
=> 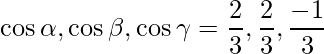
(ii): 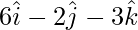
Solution:
The direction ratios are given as 6, -2 and -3.
Direction cosines are given as,
=> 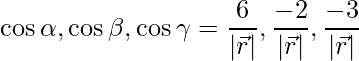
=> 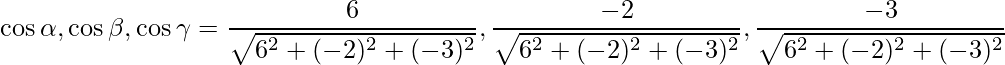
=> 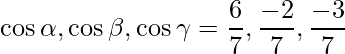
(iii): 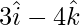
Solution:
The direction ratios are given as 3, 0 and -4.
Direction cosines are given as,
=> 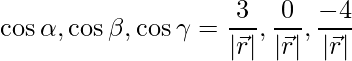
=> 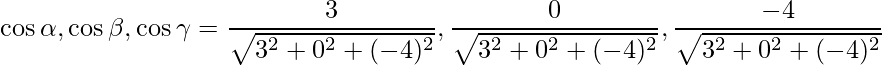
=> 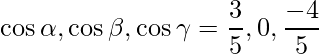
Question 7: Find the angles at which the following vectors are inclined to each of the coordinates axes.
(i): 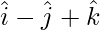
Solution:
The given direction ratios are: 1,-1,1.
Thus,
=> 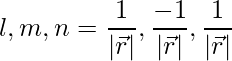
=> 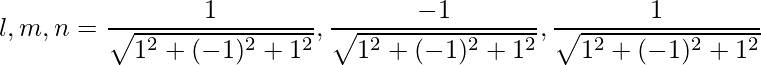
=> 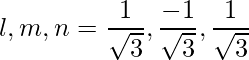
=> 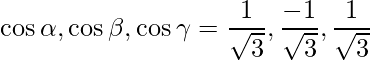
=> 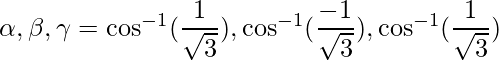
(ii): 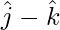
Solution:
The given direction ratios are: 0,1,-1.
Thus,
=> 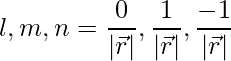
=> 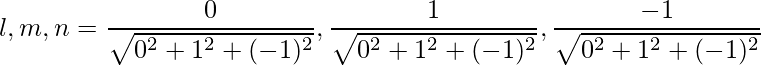
=> 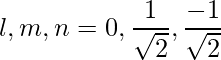
=> 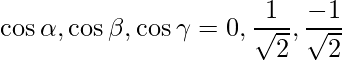
=> 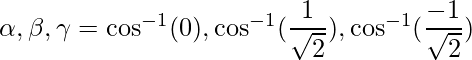
=> 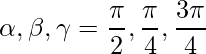
(iii): 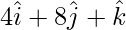
Solution:
The given direction ratios are: 4, 8, 1.
Thus,
=> 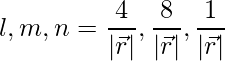
=> 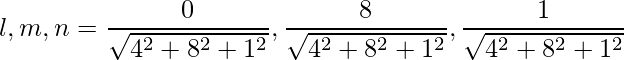
=> 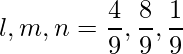
=> 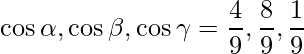
=> 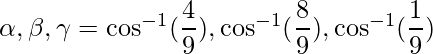
Question 8: Show that the vector 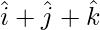 is equally inclined with the axes OX, OY and OZ.
is equally inclined with the axes OX, OY and OZ.
Solution:
Let 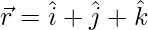
Thus, 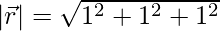
=> 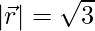
Thus the direction cosines are: 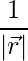 ,
, 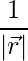 and
and 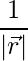
=> 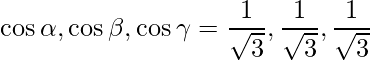
Thus,
=>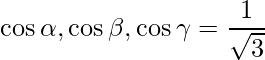
=> Thus, the vector is equally inclined with the 3 axes.
Question 9: Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ are 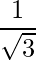 ,
,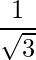 ,
, 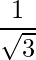 .
.
Solution:
Let the vector be equally inclined at an angle of 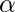 .
.
Then the direction cosines of the vector l, m, n are: 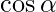 ,
, 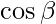 and
and 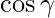
We know that,
=> l2 + m2 + n2 = 1
=> 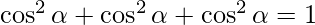
=> 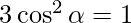
=> 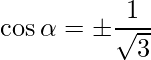
=> Thus the direction cosines are: 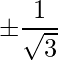 ,
, 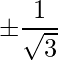 ,
, 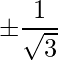 .
.
Question 10: If a unit vector  makes an angle
makes an angle  with
with 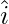 ,
, 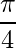 with
with 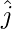 and an acute angle
and an acute angle 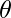 with
with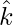 , then find \theta and hence the components of
, then find \theta and hence the components of  .
.
Solution:
The unit vector be,
=> 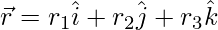
=> 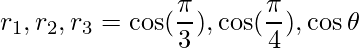
Given that 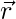 is unit vector,
is unit vector,
=> 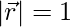
=> 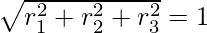
=>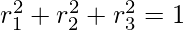
=> 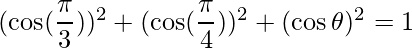
=> ![Rendered by QuickLaTeX.com (\cos \theta)^2 = 1-[\dfrac{1}{2}+\dfrac{1}{4}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6e7c5721bc9b3df9932d5456f3d2448d_l3.png)
=> 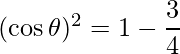
=> 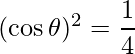
=> 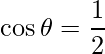
=> 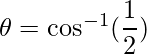
=> 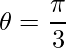
Question 11: Find a vector 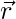 of magnitude
of magnitude 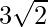 units which makes an angle of
units which makes an angle of 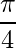 and
and 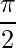 with y and z axes respectively.
with y and z axes respectively.
Solution:
Let l, m, n be the direction cosines of the vector 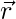 .
.
We know that,
=> l2 + m2 + n2 = 1
=> 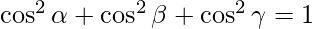
=> ![Rendered by QuickLaTeX.com l^2 =1 - [(\dfrac{1}{\sqrt{2}})^2+(0)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7974ed6442dd6f3ae0c7efea13d5b062_l3.png)
=> 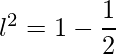
=> 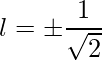
Thus vector is,
=> 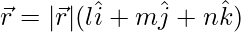
=> 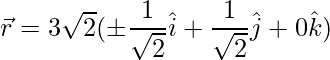
=> 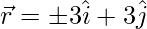
Question 12: A vector 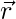 is inclined at equal angles to the 3 axes. If the magnitude of
is inclined at equal angles to the 3 axes. If the magnitude of 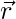 is
is 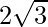 , find
, find 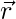 .
.
Solution:
Let l, m, n be the direction cosines of the vector 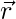 .
.
Given that the vector is inclined at equal angles to the 3 axes.
=> 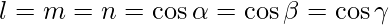
We know that,
=> l2 + m2 + n2 = 1
=> 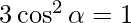
=>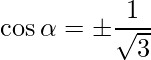
Hence, the vector is given as,
=> 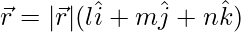
=> 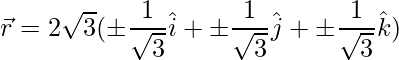
=> 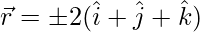
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...