Class 12 RD Sharma Solutions – Chapter 7 Adjoint and Inverse of a Matrix – Exercise 7.1 | Set 2
Last Updated :
28 Mar, 2021
Question 10. For the following parts of matrices verify that (AB)-1 = B-1A-1.
(i) A = 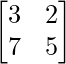 and B =
and B = 
Solution:
To prove (AB)-1= B-1A-1
We take LHS
AB = 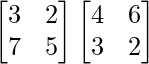
= 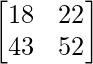
|AB| = 18 × 52 – 22 × 43
= 936 – 946 = -10
adj(AB) = 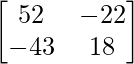
AB-1= adj(AB)/|AB| = 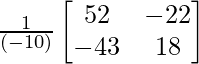
= 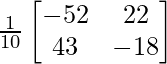
Now,
A = 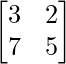
|A| = 15 – 14 = 1
adj A = 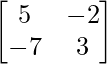
Therefore, A-1 = adj A/|A| = 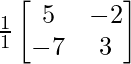
B = 
|B| = 8 – 18 = -10
adj B = 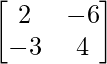
Therefore, B-1= adj B/|B| = 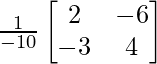
Now, we take RHS
B-1A-1 = 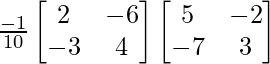
= 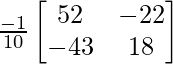
= 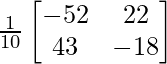
LHS = RHS
Hence, Proved
(ii) A = 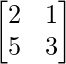 and B =
and B = 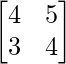
Solution:
To prove (AB)-1 = B-1A-1
We take LHS
AB = 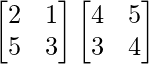
= 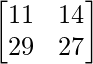
|AB| = 11 × 27 – 29 × 14
= 407 – 406 = 1
adj(AB) = 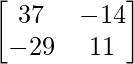
AB-1= adj(AB)/|AB| = 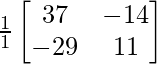
=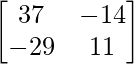
Now,
A = 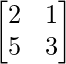
|A| = 6 – 5 = 1
adj A=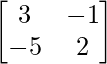
Therefore, A-1 = adj A/|A| = 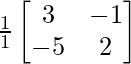
B = 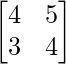
|B| = 16 – 15 = 1
adj B =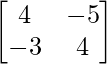
Therefore, B-1= adj B/|B| = 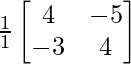
Now, we take RHS
B-1A-1 = 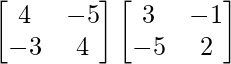
= 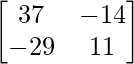
LHS = RHS
Hence, Proved
Question 11. Let A = 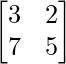 and B =
and B = 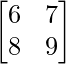 . Find (AB)-1.
. Find (AB)-1.
Solution:
AB =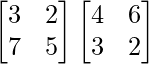
=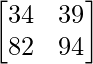
|AB| = 34 × 94 – 39 × 82 = -2
adj(AB) = 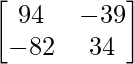
AB-1 = adj(AB)/|AB| = 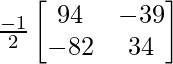
= 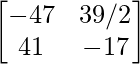
Question 12. Given A = 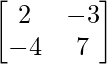 , Compute A-1 and show that 2A-1 = 9I – A.
, Compute A-1 and show that 2A-1 = 9I – A.
Solution:
A =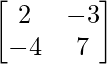
|A| = 14 – 12 = 2
adj A = 
Therefore, A-1 = adj A/|A| = 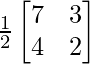
To show 2A-1 = 9I – A.
LHS = 2 × (1/2) 
= 
Now we take RHS
= 9I – A
= 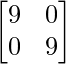 –
– 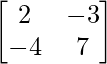
=
LHS = RHS
Hence Proved
Question 13. If A =  , then show that A – 3I = 2(I + 3A-1).
, then show that A – 3I = 2(I + 3A-1).
Solution:
Here, A = 
|A| = 4 – 10 = -6
adj A =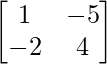
Therefore, A-1 = adj A/|A| = 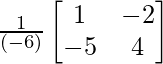
To show, A – 3I = 2(I + 3A-1)
Now we take LHS
= A – 3I
= – 3
– 3
=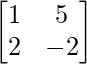
Now we take RHS
= 2I + 6A-1
= 2 + 6 × (1/6)
+ 6 × (1/6)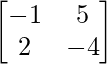
= 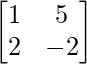
LHS = RHS
Hence Proved
Question 14. Find the inverse of the matrix A = 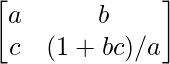 and show that aA-1 = (a2 + bc + 1)I – aA.
and show that aA-1 = (a2 + bc + 1)I – aA.
Solution:
Here, A = 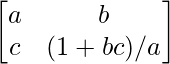
|A| = (a + abc)/a – bc = 1
Therefore, inverse of A exists
Cofactor of A are,
C11 = (1 + bc)/a C12 = -c
C21 = -b C22 = a
adj A = 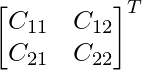
= 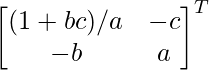
= 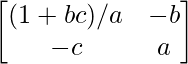
A-1 = 1/|A|. adj A
= 1/1 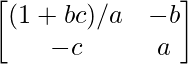
= 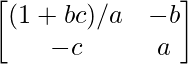
To show that
aA-1 = (a2 + bc + 1)I – aA.
LHS = aA-1
= a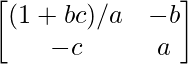
= 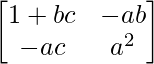
RHS = (a2 + bc + 1)I – aA
= 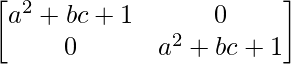 – a
– a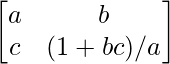
= 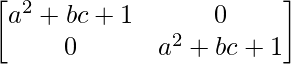 –
– 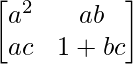
= 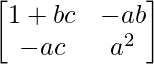
LHS = RHS
Hence Proved
Question 15. Given A = 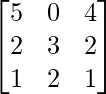 , B-1 =
, B-1 = 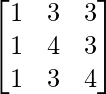 , Compute (AB)-1.
, Compute (AB)-1.
Solution:
We know (AB)-1 = B-1A-1
Here, A = 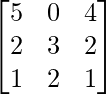
|A| = 5(3 – 4) + 4(4 – 3) = -5 + 4 = -1
Co-factors of A are:
C11 = -1 C12 = 0 C13 = 1
C21 = 8 C22 = 1 C23 = -10
C31 = -12 C32 = -2 C33 = 15
adj A = 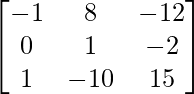
A-1 = 1/|A|. adj A
Hence, A-1 = 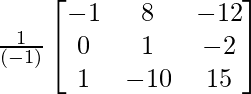
= 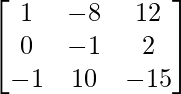
(AB)-1 = B-1A-1
= 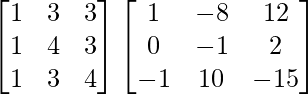
= 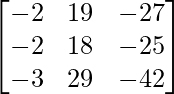
Question 16. Let F(α) = 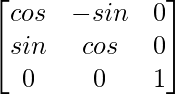 and G(β) =
and G(β) = 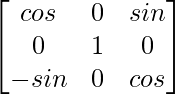 , Show that
, Show that
(i) [F(α)]-1 = F(-α)
Solution:
We have F(α) = 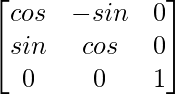
|F(α)| = cos2α + sin2α = 1
Therefore, inverse of F(α) exists
Cofactors of F(α) are:
C11 = cosα C12 = -sinα C13 = 0
C21 = sinα C22 = cosα C23 = 0
C31 = 0 C32 = 0 C33 = 1
Adj F(α) = 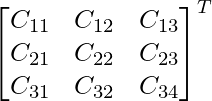
=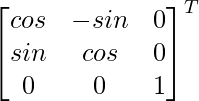
=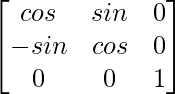
[F(α)]-1 = 1/|F(α)|. adj F(α)
Hence, [F(α)]-1 = 1/1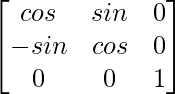
=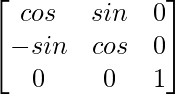
Now, F(-α) = 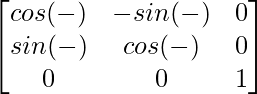
=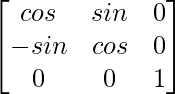
So, [F(α)]-1 = F(-α)
Hence, Proved
(ii) [G(β)]-1 = G(-β)
Solution:
We have G(β) = 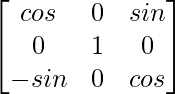
|G(β)| = cos2β + sin2β = 1
Therefore, inverse of G(β) exists
Cofactors of G(β) are:
C11 = cosβ C12 = 0 C13 = sinβ
C21 = 0 C22 = 1 C23 = 0
C31 = -sinβ C32 = 0 C33 = sinβ
Adj G(β) = 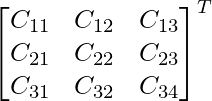
=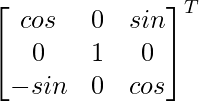
=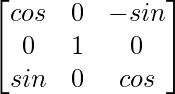
[G(β)]-1 = 1/|G(β)|. adj G(β)
Hence, [G(β)]-1 = 1/1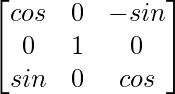
= 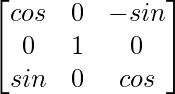
Now, G(-β) =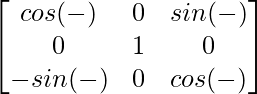
= 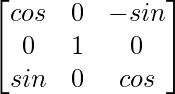
So, [G(β)]-1 = G(-β)
Hence, Proved
(iii) [F(α)G(β)]-1 = F(-α)G(-β)
Solution:
We already know that S[G(β)]-1 = G(-β)
[F(α)]-1 = F(-α)
Taking LHS = [F(α)G(β)]-1
= [F(α)]-1[G(β)]-1
= F(-α)G(-β) = RHS
Hence, Proved
Question 17. If A =  , Verify that A2 – 4A + I = O, where I =
, Verify that A2 – 4A + I = O, where I =  and O =
and O =  , Hence, find A-1.
, Hence, find A-1.
Solution:
Here, A = 
A2 = 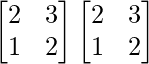
= 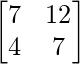
4A = 4
= 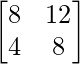
A2 – 4A + I = O
= 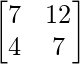 –
–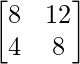 +
+ 
= 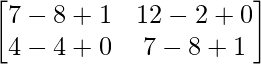
Hence, = 
Now, A2 – 4A + I = O
A2 – 4A = -I
Multiplying both side by A-1 both sides we get
A.A(A-1) – 4AA-1 = -IA-1
AI – 4I = -A-1
A-1 = 4I – AI
= 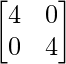 –
– 
= 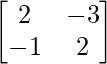
Question 18. Show that A = 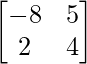 satisfies the equation A2 + 4A – 42I = O. Hence, Find A-1.
satisfies the equation A2 + 4A – 42I = O. Hence, Find A-1.
Solution:
Here, A = 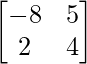
A2 = 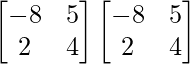
=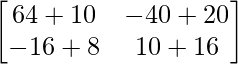
=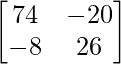
4A = 4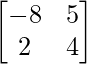
= 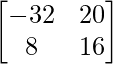
A2 + 4A – 42I = 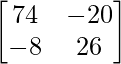 +
+ 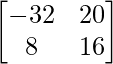 –
– 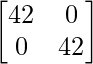
=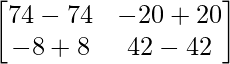
Hence, 
Now, A2 + 4A – 42I = 0
⇒ A-1A.A + 4A-1.A – 42A-1I = 0
⇒ IA + 4I – 42A-1 = 0
⇒ A-1 = 1/42 [A + 4I]
⇒ A-1 = 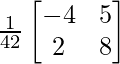
Question 19. If A = 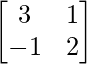 , show that A2 – 5A + 7I = O. Hence find A-1.
, show that A2 – 5A + 7I = O. Hence find A-1.
Solution:
Here, A = 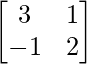
A2 = 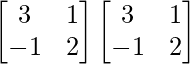
=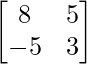
Now, A2 – 5A + 7I = 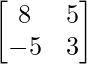 + 5
+ 5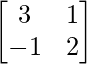 + 7
+ 7
=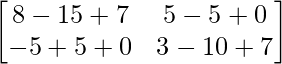
=
Now, A2 – 5A + 7I = O
Multiplying by A-1 both sides
⇒ A-1AA + 5AA – 1 + 7IA-1 = 0
⇒ A-1 = 1/7[5I – A]
⇒ A-1 = 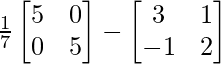
⇒ A-1 = 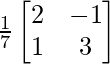
Question 20. If A = 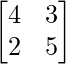 , find x and y such that A2 – xA + yI = O. Hence, evaluate A-1.
, find x and y such that A2 – xA + yI = O. Hence, evaluate A-1.
Solution:
Here, A = 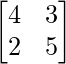
A2 = 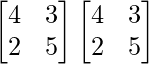
= 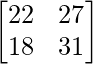
Now, A2 – xA + yI = O
⇒ 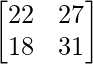 –
– 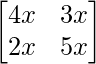 +
+ 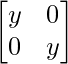
= 
⇒ 22 – 4x + y = 0
⇒ 4x – y = 22 ………(i)
or
18 – 2x = 0
⇒ x = 9
Putting x = 9 in eq (i)
⇒ y = 14
A2 – 9A + 14I = 0
⇒ 9A = A2 + 14I
⇒ 9A-1A = A-1AA + 14A-1
⇒ 9I = IA + 14A-1
⇒ A-1 = 1/14[9I – A] = 1/14(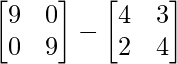 )
)
⇒ A-1= 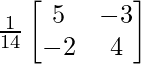
Question 21. If A = 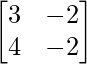 , find the value of λ so that A2 = λA – 2I. Hence, find A-1.
, find the value of λ so that A2 = λA – 2I. Hence, find A-1.
Solution:
Here, A = 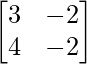
A2 = 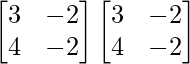
= 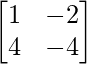
If A2 = λA – 2I
λA = A2 + 2I
⇒ λ 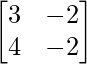 =
= 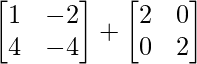
⇒ λ 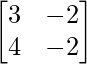 =
= 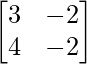
⇒ λ = 1
Now, A2 = λA – 2I
Multiplying both side A-1
⇒ A-1AA = A-1A – 2A-1I
⇒ A = I – 2A-1
⇒ 2A-1 = I – A = 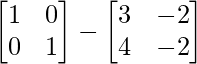
A-1 = 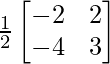
Question 22. Show that A = 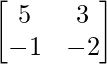 satisfies the equation x2 – 3x – 7 = 0. Thus, find A-1.
satisfies the equation x2 – 3x – 7 = 0. Thus, find A-1.
Solution:
Here, A = 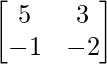
A2 = 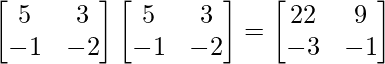
Now, A2 – 3A – 7= 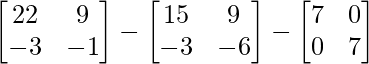
=
We have, A2 – 3A – 7 = 0
⇒ A-1AA – 3A-1A – 7A-1 = 0
⇒ A-3I – 7A-1 = 0
⇒ 7A-1 = A – 3I
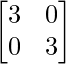
⇒ 7A-1 = 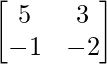 –
– 
A-1 = 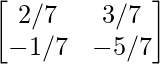
Question 23. Show that A =  satisfies the equation x2 – 12x + 1 = 0. Thus, find A-1.
satisfies the equation x2 – 12x + 1 = 0. Thus, find A-1.
Solution:
Here, A = 
A2 = 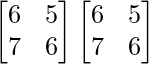
= 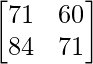
Now, A2 – 12A + I =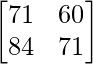 –
– 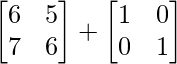
=
We have, A2 – 12A + I = 0
⇒ A – 12I + A-1 = 0
⇒ A-1 = 12I – A
⇒ A-1 = 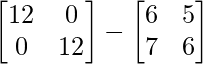
⇒ A-1 = 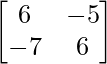
Question 24. For the matrix A =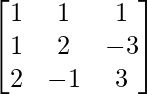 show that A3 – 6A2 + 5A + 11I3 = O. Hence, find A-1.
show that A3 – 6A2 + 5A + 11I3 = O. Hence, find A-1.
Solution:
Here, A =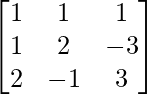
A2 = 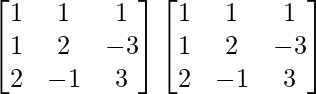
= 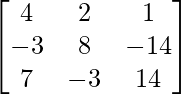
A3 = 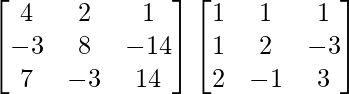
= 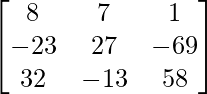
A3 – 6A2 + 5A + 11I
= 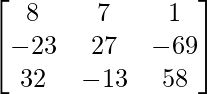 – 6
– 6 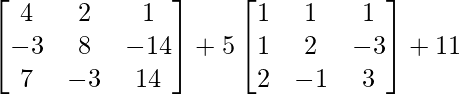
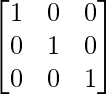
=
= 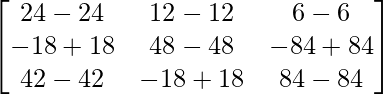
= 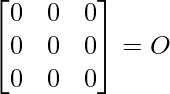
We have, A3 – 6A2 + 5A + 11I = O.
⇒ A-1(AAA) – 6A-1(AA) + 5A-1A + 11IA-1 = 0
⇒ A2 – 6A + 5I = -11A-1
⇒ -11A-1 = (A2 – 6A + 5I)
=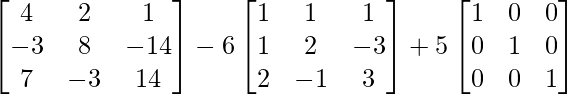
=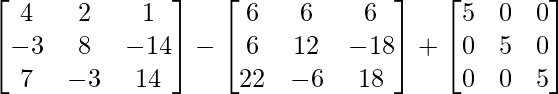
=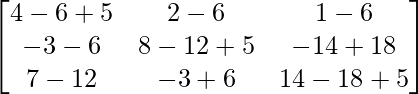
=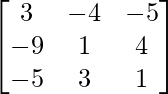
Therefore, A-1 = 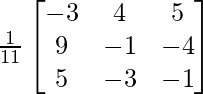
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...