Question 1. Show that the three lines with direction cosines 12/13, -3/13, – 4/13; 4/13, 12/13, 3/13; 3/13, – 4/13, 12/13 are mutually perpendicular.
Solution:
The direction cosines of the three lines are
l1 = 12/13, m1 = -3/13, n1 = -4/13
l2 = 4/13, m2 = 12/13, n2 = 3/13
l3 = 3/13, m3 = -4/13, n3 = 12/13
So, l1 l2 + m1 m2 + n1 n2 =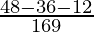 = 0
= 0
Also,
l2 l3 + m2 m3 + n2 n3 =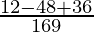 = 0
= 0
l1 l3 + m1 m3 + n1 n3 =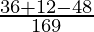 = 0
= 0
Therefore, the given lines are perpendicular to each other.
Hence proved.
Question 2. Show that the line through the points (1, −1, 2) and (3, 4, −2) is perpendicular to the through the points (0, 3, 2) and (3, 5, 6).
Solution:
We have,
 is passing through the points (1, -1, 2) and (3, 4, -2).
is passing through the points (1, -1, 2) and (3, 4, -2).
Also, is passing through the points (0, 3, 2) and (3, 5, 6).
is passing through the points (0, 3, 2) and (3, 5, 6).
Then,
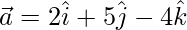
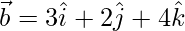
Now,
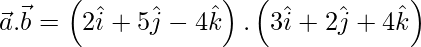
= 6 + 10 – 16
= 0
Therefore, the given lines are perpendicular to each other.
Hence proved.
Question 3. Show that the line through the points (4, 7, 8) and (2, 3, 4) is parallel to the line through the points (−1, −2, 1) and, (1, 2, 5).
Solution:
Equations of lines passing through the points (x1, y1, z1) and (x2, y2, z2) are given by
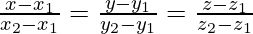
So, the equation of a line passing through (4, 7, 8) and (2, 3, 4) is
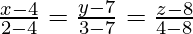
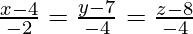
Also, the equation of the line passing through the points ( -1, -2,1) and (1, 2, 5) is
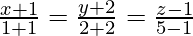
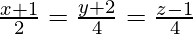
We know that two lines are parallel if,
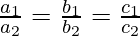
And the Cartesian equations of the two lines are given by,
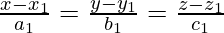
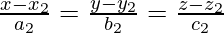
So, we get,
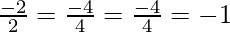
Therefore, the given lines are parallel to each other.
Hence proved.
Question 4. Find the cartesian equation of the line which passes through the point (−2, 4, −5) and parallel to the line given by 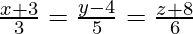 .
.
Solution:
We know that the cartesian equation of a line passing through a point with position vector and parallel to the vector
and parallel to the vector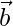 is given by,
is given by,
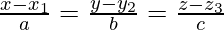
Here,
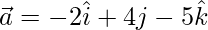
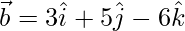
The cartesian equation of the required line is,
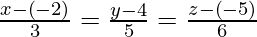
=>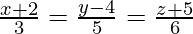
Question 5. Show that the lines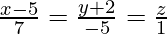 and
and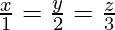 are perpendicular to each other.
are perpendicular to each other.
Solution:
We have
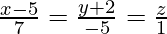
And also,
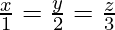
These equations can be re-written as,
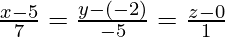 . . . . (1)
. . . . (1)
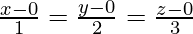 . . . . (2)
. . . . (2)
Therefore, the vector parallel to line (1) is given by,
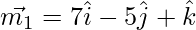
And the vector parallel to line (2) is given by,
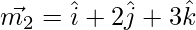
Now,
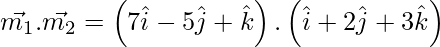
= 7 – 10 + 3
= 0
Therefore, the given two lines are perpendicular to each other.
Hence proved.
Question 6. Show that the line joining the origin to the point (2, 1, 1) is perpendicular to the line determined by the points (3, 5, −1) and (4, 3, −1).
Solution:
The direction ratios of the line joining the origin to the point (2, 1, 1) are 2, 1, 1.
Let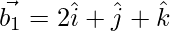
The direction ratios of the line joining the points (3, 5, -1) and (4, 3, -1) are 1, -2, 0.
Let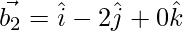
Now,
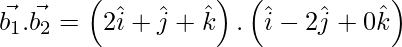
= 2 – 2 + 0
= 0
So, we get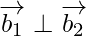 .
.
Therefore, the two lines joining the given points are perpendicular to each other.
Hence proved.
Question 7. Find the equation of a line parallel to x-axis and passing through the origin.
Solution:
The direction ratios of the line parallel to x-axis are proportional to 1, 0, 0.
Equation of the line passing through the origin (0, 0, 0) and parallel to x-axis is
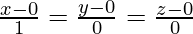
=>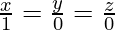
Question 8. Find the angle between the following pair of line:
(i)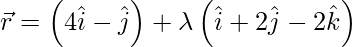 and
and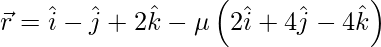
Solution:
We have,
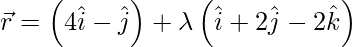
And also,
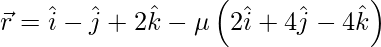
Let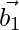 and
and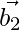 be vectors parallel to the given lines .
be vectors parallel to the given lines .
Now,
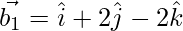
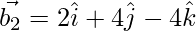
If θ is the angle between the given lines, then
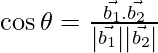
=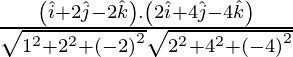
=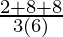
= 1
As cos θ = 1
=> θ = 0°
Therefore, the angle between two lines is 0°.
(ii)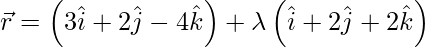 and
and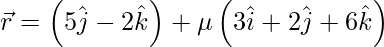
Solution:
We have,
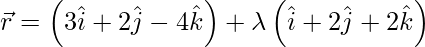
And also,
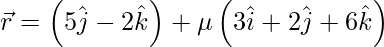
Let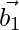 and
and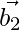 be vectors parallel to the given lines .
be vectors parallel to the given lines .
Now,
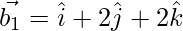
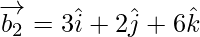
If θ is the angle between the given line, then
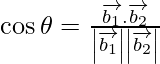
=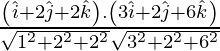
=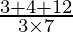
= 19/21
As cos θ = 19/21
=> θ = cos-1 (19/21)
Therefore, the angle between two lines is cos-1 (19/21).
(iii)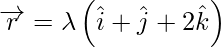 and
and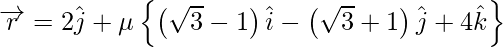
Solution:
We have,
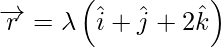
And also,
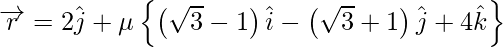
Let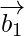 and
and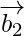 be vector parallel to the given line.
be vector parallel to the given line.
Now,
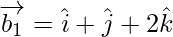
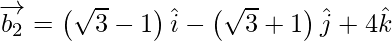
If θ is the angle between the given line, then
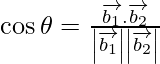
=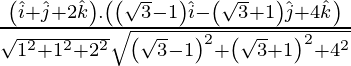
=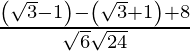
= 6/12
= 1/2
As cos θ = 1/2
=> θ = π/3
Therefore, the angle between two lines is π/3.
Question 9. Find the angle between the following pair of line:
(i)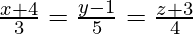 and
and 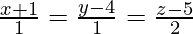
Solution:
We have,
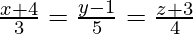
And also,
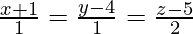
Let,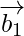 and
and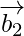 be vectors parallel to the given line.
be vectors parallel to the given line.
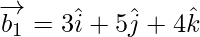
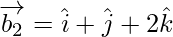
If θ is the angle between the given line, then
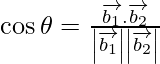
=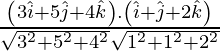
=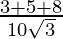
= 8/5√3
As cos θ = 8/5√3
=> θ = cos-1 (8/5√3)
Therefore, the angle between two lines is cos-1 (8/5√3).
(ii)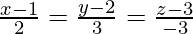 and
and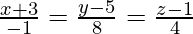
Solution:
We have,
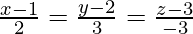
And also,
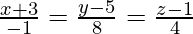
Let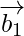 and
and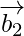 be vectors parallel to the given lines.
be vectors parallel to the given lines.
Now,
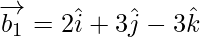
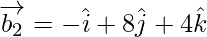
If θ is the angle between the given lines, then
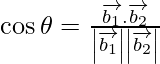
=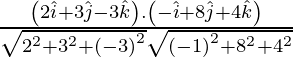
=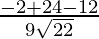
=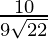
As cos θ =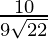
=> θ =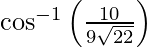
Therefore, the angle between two lines is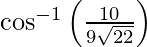 .
.
(iii)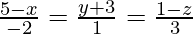 and
and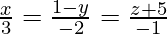
Solution:
We have,
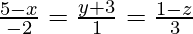
And also,
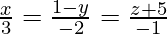
The equation of the given line can be re-written as
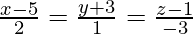
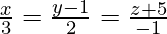
Let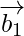 and
and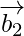 be vectors parallel to the given lines.
be vectors parallel to the given lines.
Now,
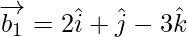
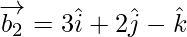
If θ is the angle between the given lines, then
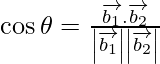
=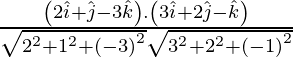
=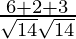
= 11/14
As cos θ = 11/14
=> θ = cos-1 (11/14)
Therefore, the angle between two lines is cos-1 (11/14).
(iv) and
and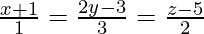
Solution:
We have,
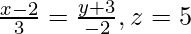
And also,
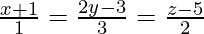
The equations of the given lines can be re-written as
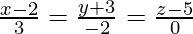
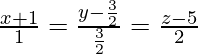
Let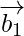 and
and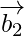 be vectors parallel to the given lines.
be vectors parallel to the given lines.
Now,
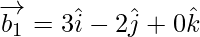
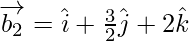
If θ is the angle between the given lines, then
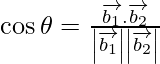
=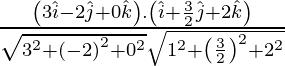
=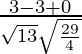
= 0
As cos θ = 0
=> θ = π/2
Therefore, the angle between two lines is π/2.
(v)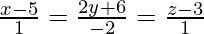 and
and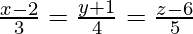
Solution:
We have,
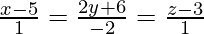
And also,
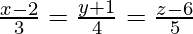
The equations of the given lines can be re-written as,
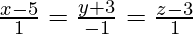
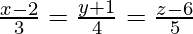
Let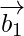 and
and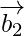 be vectors parallel to the given lines.
be vectors parallel to the given lines.
Now,
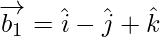
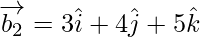
If θ is the angle between the given lines, then
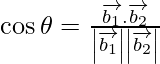
=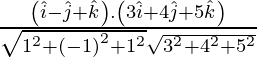
=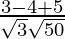
= 4/5√6
As cos θ = 4/5√6
=> θ = cos-1 (4/5√6)
Therefore, the angle between two lines is cos-1 (4/5√6).
(vi)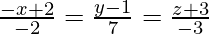 and
and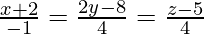
Solution:
We have,
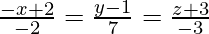
And also,
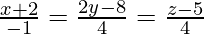
The equations of the given lines can be re-written as
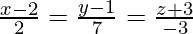
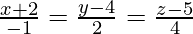
Let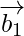 and
and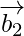 be vectors parallel to the given lines.
be vectors parallel to the given lines.
Now,
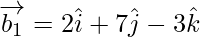
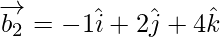
If θ is the angle between the given lines, then
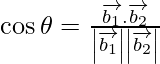
=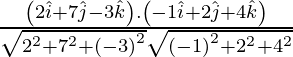
=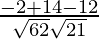
= 0
As cos θ = 0
=> θ = π/2
Therefore, the angle between two lines is π/2.
Question 10. Find the angle between the pairs of lines with direction ratios proportional to:
(i) 5, −12, 13 and −3, 4, 5
Solution:
We have pairs of lines with direction ratios proportional to 5, −12, 13 and −3, 4, 5.
Let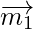 and
and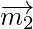 be vectors parallel to the two given lines.
be vectors parallel to the two given lines.
Then, the angle between the two given lines is same as the angle between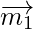 and
and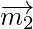 .
.
Now,
The vector parallel to the line having direction ratios proportional to 5, – 12, 13 is,
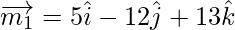
And the vector parallel to the line having direction ratios proportional to -3, 4, 5 is,
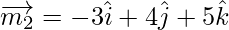
Let θ be the angle between the lines.
Now,
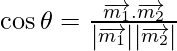
=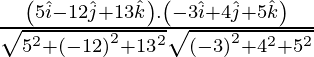
=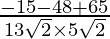
= 1/65
As cos θ = 1/65
=> θ = cos-1 (1/65)
Therefore, the angle between two lines is cos-1 (1/65).
(ii) 2, 2, 1 and 4, 1, 8
Solution:
We have pairs of lines with direction ratios proportional to 2, 2, 1 and 4, 1, 8.
Let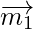 and
and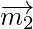 be vectors parallel to the given two lines.
be vectors parallel to the given two lines.
Then, the angle between the lines is same as the angle between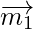 and
and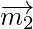 .
.
Now,
The vector parallel to the line having direction ratios proportional to 2, 2, 1 is,
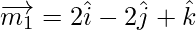
And the vector parallel to the line having direction ratios proportional to 4, 1, 8 is,
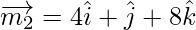
Let θ be the angle between the lines.
Now,
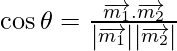
=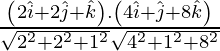
=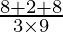
= 2/3
As cos θ = 2/3
=> θ = cos-1 (2/3)
Therefore, the angle between two lines is cos-1 (2/3).
(iii) 1, 2, −2 and −2, 2, 1
Solution:
We have pairs of lines with direction ratios proportional to 1, 2, −2 and −2, 2, 1.
Let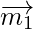 and
and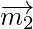 be vectors parallel to the two given lines.
be vectors parallel to the two given lines.
Then, the angle between the two given lines is same as the angle between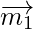 and
and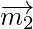 .
.
Now,
The vector parallel to the line having direction ratios proportional to 1, 2, – 2 is,
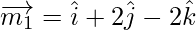
And the vector parallel to the line having direction ratios proportional to -2, 2, 1 is,
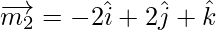
Let θ be the angle between the lines.
Now,
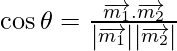
=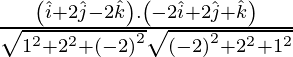
=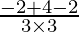
= 0
As cos θ = 0
=> θ = π/2
Therefore, the angle between two lines is π/2.
(iv) a, b, c and b − c, c − a, a − b
Solution:
We have pairs of lines with direction ratios proportional to a, b, c and b − c, c − a, a − b.
Let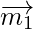 and
and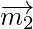 be vectors parallel to the given two lines.
be vectors parallel to the given two lines.
Then, the angle between the two lines is same as the angle between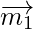 and
and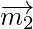 .
.
Now,
The vector parallel to the line having direction ratios proportional to a, b, c is,
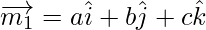
And the vector parallel to the line having direction ratios proportional to b – c, c – a, a – b is,
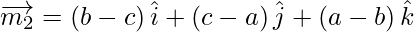
Let θ be the angle between the lines.
Now,
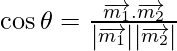
=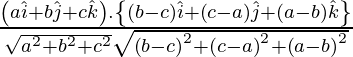
=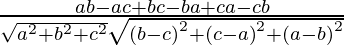
= 0
As cos θ = 0
=> θ = π/2
Therefore, the angle between two lines is π/2.
Question 11. Find the angle between two lines, one of which has direction ratios 2, 2, 1 while the other one is obtained by joining the points (3, 1, 4) and (7, 2, 12).
Solution:
The direction ratios of the line joining the points (3, 1, 4) and (7, 2, 12) are proportional to 4, 1, 8.
Let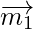 and
and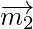 be vectors parallel to the lines having direction ratios proportional to 2, 2, 1 and 4, 1, 8.
be vectors parallel to the lines having direction ratios proportional to 2, 2, 1 and 4, 1, 8.
Now,
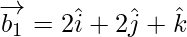
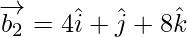
If θ is the angle between the given lines, then
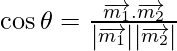
=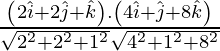
=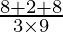
= 2/3
As cos θ = 2/3
=> θ = cos-1 (2/3)
Therefore, the angle between two lines is cos-1 (2/3).
Question 12. Find the equation of the line passing through the point (1, 2, −4) and parallel to the line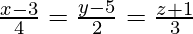 .
.
Solution:
The direction ratios of the line parallel to line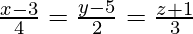 are proportional to 4, 2, 3.
are proportional to 4, 2, 3.
Equation of the required line passing through the point (1, 2,-4) having direction ratios proportional to 4, 2, 3 is
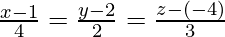
=>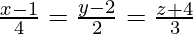
Share your thoughts in the comments
Please Login to comment...