Class 12 RD Sharma Solutions- Chapter 28 The Straight Line in Space – Exercise 28.4
Last Updated :
14 Nov, 2022
Question 1. Find the perpendicular distance of the point (3, -1, 11) from the line 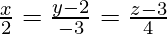
Solution:
Let the foot of the perpendicular drawn from P (3, -1, 11) to the line 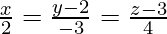 is Q, so we have to find length of PQ is general point on the line
is Q, so we have to find length of PQ is general point on the line 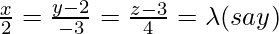
Coordinate of Q = 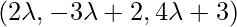 , direction ratios of the given line = 2,-3,4. Since PQ is the perpendicular to the given line interface.
, direction ratios of the given line = 2,-3,4. Since PQ is the perpendicular to the given line interface.
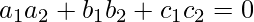
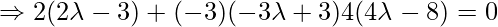
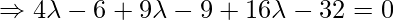
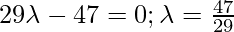
So, the coordinates of Q are:
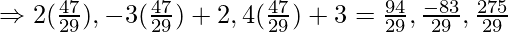
Distance between P and Q is given as:
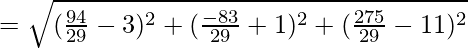
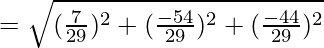
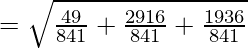
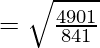
So, the required distance is 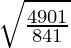 units
units
Question 2. Find the perpendicular distance of the point (1,0,0) from the line 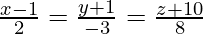 . Also, find the coordinates of the foot of the perpendicular and the equation of the perpendicular.
. Also, find the coordinates of the foot of the perpendicular and the equation of the perpendicular.
Solution:
Let us consider the foot of the perpendicular drawn from P (1,0,0) to the line 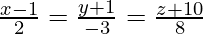 is Q. So let us find the length of PQ i.e.
is Q. So let us find the length of PQ i.e. 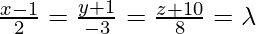
Coordinate of Q = 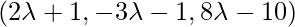
The direction ratios of the given line: 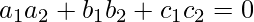
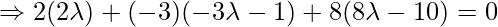
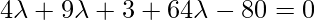
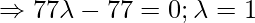
So the Coordinates of Q are as follows:
![Rendered by QuickLaTeX.com (2\lambda+1, -3\lambda-1, 8\lambda-10)= [2(1)+1,-3(1)-1,8(1)-10]= [3,4,-2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d275fd734406bf6af3e3658bf4b8529_l3.png)
Distance between P and Q is given by:
PQ = 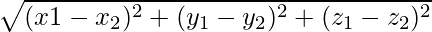
PQ = 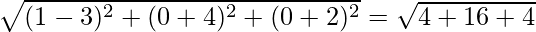
PQ = 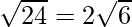
Hence, the foot of the perpendicular = (3,-4,-2);
Length of the perpendicular = 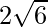 units.
units.
Question 3. Find the foot of the perpendicular drawn from the point A(1,0,3) to the joint of the points B(4,7,1) and C(3,5,3).
Solution:
Let us consider, the foot of the perpendicular drawn from A(1,0,3) to the line joining
Points B(4,7,1) and C(3,5,3) be D. The equation of the line passing through
points B(4,7,1) and C(3,5,3) is
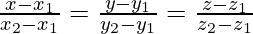
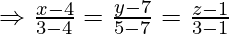
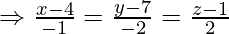
Let 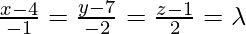
So, the direction ratio of AD is 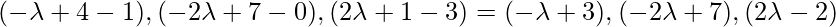
Line AD is the perpendicular to BC so, 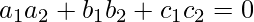
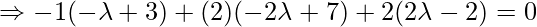
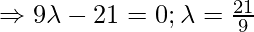
Hence, coordinates of D are: 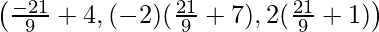
= 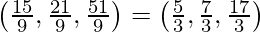
Question 4. A (1,0,4), B (0,-11,3), C (2,-3,1) are three points and D is the foot of the perpendicular from A on BC. Find the coordinates of D.
Solution:
Given: D is the perpendicular from A(1,0,4) on BC. So,
Equation of line passing through BC is:
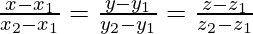
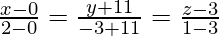
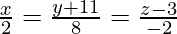
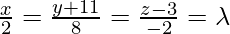
Coordinates of D = ( 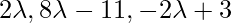 )
)
Direction ratios of AD is 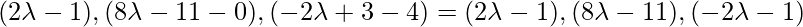
Line AD is perpendicular to BS so,
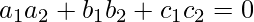
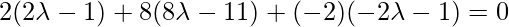
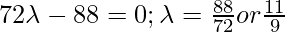
So, coordinates of D are = 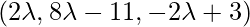
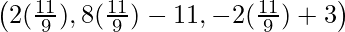 =
=
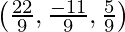
Question 5. Find the foot of the perpendicular from the point (2,3,4) to the line 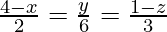 . Also, find the perpendicular distance from the given point to the line.
. Also, find the perpendicular distance from the given point to the line.
Solution:
Let us consider that The foot of the perpendicular drawn from P(2,3,4) to the line
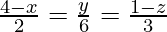 is
is 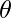 .
.
Equation of the line is 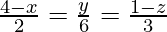
Let 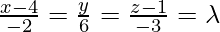
Coordinates of Q = 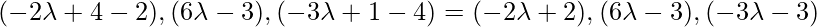
So, PQ is perpendicular to the given line, 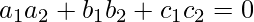
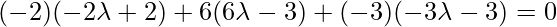
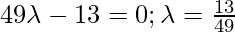
Coordinates of Q = 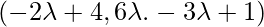
= 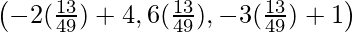
= 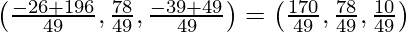
Distance between P and Q is given by: PQ = 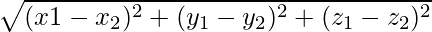
= 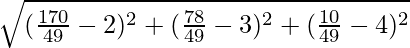
= 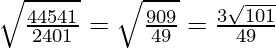
Hence, perpendicular distance from (2,3,4) to the given line is 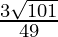 units.
units.
Question 6. Find the equation of the perpendicular drawn from the point P (2,4,-1) to the line 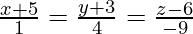 . Also, write down the coordinates of the foot of the perpendicular from P.
. Also, write down the coordinates of the foot of the perpendicular from P.
Solution:
Let 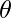 be the foot of the perpendicular drawn from P(2,4,-1) to the line
be the foot of the perpendicular drawn from P(2,4,-1) to the line
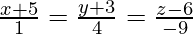
Given line is 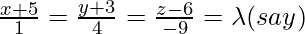
Coordinate of Q (General point on the line) = 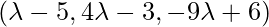
Direction ratios of PQ are: 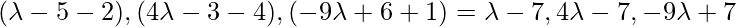
As line PQ is perpendicular to the given line, so: 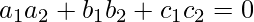
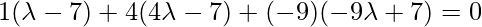
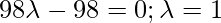
Therefore, coordinates of foot of perpendicular = {-4, 1, -3}
So equation of the perpendicular PQ is : 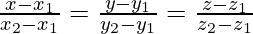
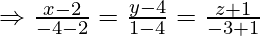
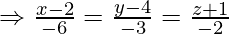
Question 7. Find the length of the perpendicular drawn from the point (5,4,-1) to the line 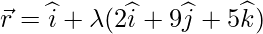
Solution:
Let the foot of the perpendicular drawn from P(5,4,-1) to the given line is Q, so given equation of line is:
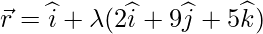
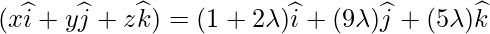
Equating the coefficients of 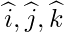
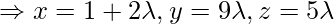
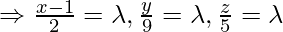
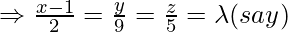
Coordinate of Q = 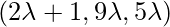
Direction ratios of line PQ are: 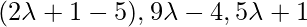
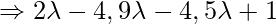
As line PQ is perpendicular to the given line, so: 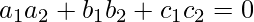
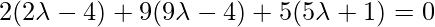
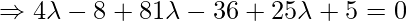
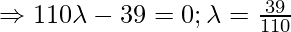
Coordinate of Q = { 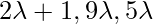 }
}
= 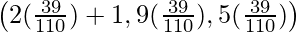
= 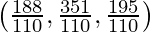
Length of perpendicular = PQ = 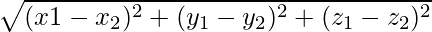
= 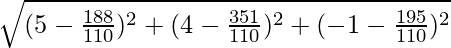
PQ = 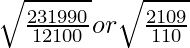
Question 8. Find the foot of the perpendicular drawn from the point 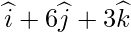 to the line
to the line 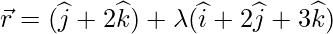 . Also, find the length of the perpendicular.
. Also, find the length of the perpendicular.
Solution:
Let position vector of foot of perpendicular drawn from p 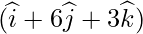 on
on 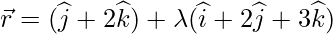 be Q
be Q 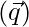 . So, Q is on the line
. So, Q is on the line 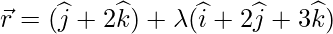
So, position vector of Q = 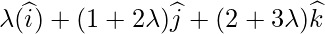
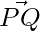 is the position vector of Q – position vector of p =
is the position vector of Q – position vector of p = 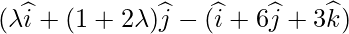
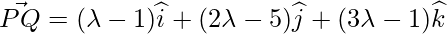
Here, PQ vector is perpendicular to the given line. So,
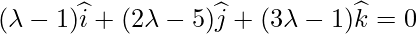
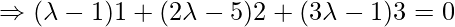
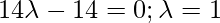
Position vector of Q = {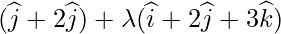 }
}
= 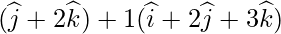
Foot of the perpendicular = 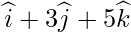
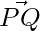 = Position vector of Q – Position vector of P
= Position vector of Q – Position vector of P
= 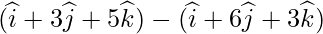
= 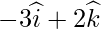
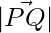 =
= 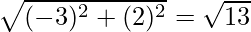 units
units
Question 9. Find the equation of the peprendicular drwan from the point P (-1,3,2) to the line 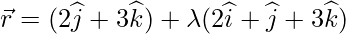 . Also, find the coordinates of the foot of the perpendicular from P.
. Also, find the coordinates of the foot of the perpendicular from P.
Solution:
Let Q be the perpendicular drawn from P {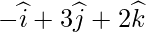 } on the
} on the
vector 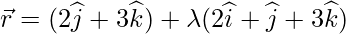
Let the position vector of Q be : 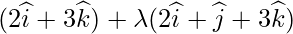
: 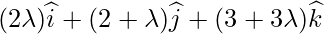
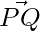 = Position Vector of Q – Position Vector of P =
= Position Vector of Q – Position Vector of P = 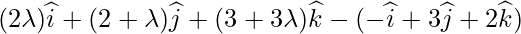
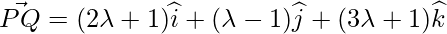
As PQ vector is perpendicular to the given line,
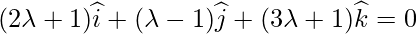
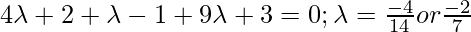
Position Vector of Q = 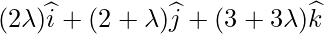 is
is
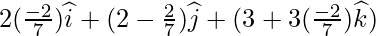
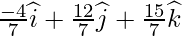
Coordinates of foot of the perpendicular: 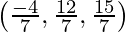
Equation of PQ is: 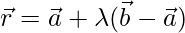
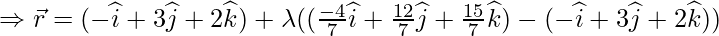
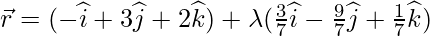
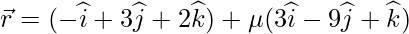
Question 10. Find the foot of the perpendicular from (0,2,7) on the line 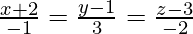
Solution:
Let the foot of the perpendicular drawn from (0,2,7) to the line 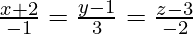 be Q.
be Q.
Given equation of the line is 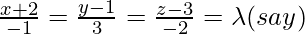
Coordinate of Q = {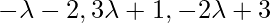 }
}
Direction Ratios of PQ are 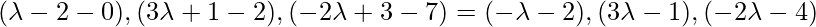
Since, PQ is perpendicular to the given line, so 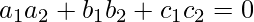
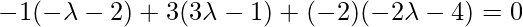
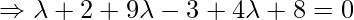
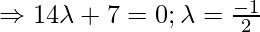
Foot of the perpendicular = {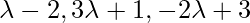 }\
}\
= 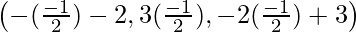
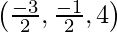
Question 11. Find the foot of the perpendicular from (1,2,-3) to the line 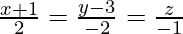
Solution:
Let the foot of perpendicular from P (1,2,-3) to the line 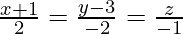 be Q.
be Q.
Given the equation of line is 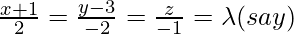
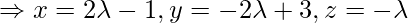
Coordinates of Q are {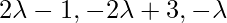 }
}
Direction Ratios of PQ are: 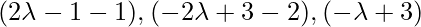 =
=
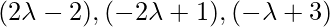
Let PQ be the perpendicular to the given line, so 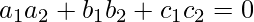
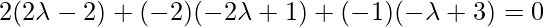
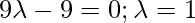
Coordinate of the perpendicular: 
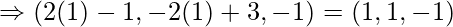
Question 12. Find the equation of the line passing through the points A (0,6,-9) and B (-3, 6, 3). If D is the foot of the perpendicular drawn from a point C (7,4,-1) on the line AB, then find the coordinates of the point D and the equation of the line CD.
Solution:
Equation of line AB is 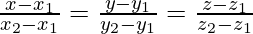
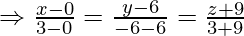
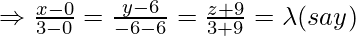
Coordinate of point D = {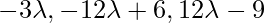 }
}
Direction ratios of CD = 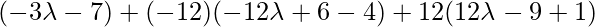
= 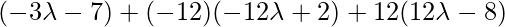
As line CD is perpendicular to the line AB, so 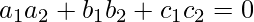
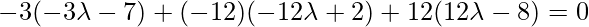
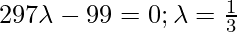
Coordinate of D = {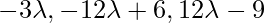 }
}
= {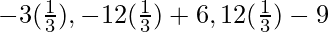 }
}
= (-1,2,-5)
Equation of CD is 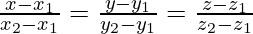
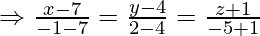
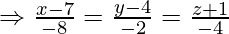
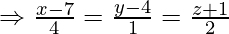
Question 13. Find the distance of the point (2,4,-1) from the line 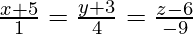
Solution:
Let P = (2,4,-1)
In order to find the distance we need to find a point Q on the line. We see that line is passing through
the point Q(-5,-3,6). So, let’s take this point as the required point.
The line is also parallel to the vector 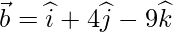
Now, 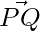 =
= 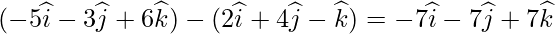
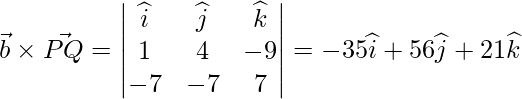
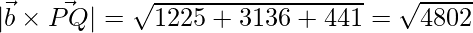
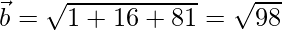
Therefore, 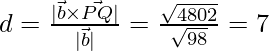
Question 14. Find the coordinates of the foot of the perpendicular drawn from point A (1,8,4) to the line joining the points B (0,-1,3) and C (2,-3,-1).
Solution:
Let L be the foot of the perpendicular drawn from A(1,8,4) on the line joining the points B(0,-1,3) and C(2,-3,-1).
Equation of the line passing through the points B and C is given by
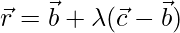
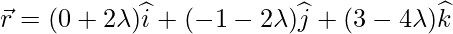
Let position vector of L be,
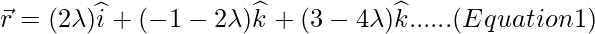
Then, 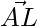 = Position vector of L – Position vector of A
= Position vector of L – Position vector of A
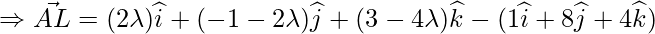
Since, AL vector is perpendicular to the given line
which is parallel to 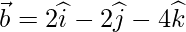
Therefore, 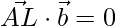
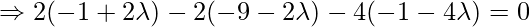
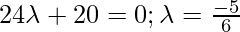
Putting value of lambda in Equation 1, we get:
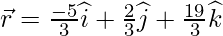
So, coordinates of foot of the perpendicular are
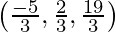
Share your thoughts in the comments
Please Login to comment...