Class 11 RD Sharma Solutions – Chapter 23 The Straight Lines- Exercise 23.12 | Set 3

Question 21. Find the coordinates of the foot of the perpendicular from the point (-1, 3) to the line 3x – 4y – 16 = 0.

Solution:

Let us considered the foot of perpendicular of P(-1, 3) on line 3x – 4y = 16 be Q(a, b)

So, (slope of given line) x (slope of PQ) = -1

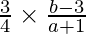
3(b – 3) = -4a – 4

3b – 9 = -4a – 4

4a + 3b = 5            …….(1)

It is given that Q(a, b) lie on the line 3x – 4y = 16

3a – 4b = 16         …….(2)

On solving eq(1) and (2), we get

a = (68/25) and b = (-49/25)

Hence, the coordinate of Q is (68/25, -49/25)

Question 22. Find the projection of the point (1, 0) on the line joining the points (-1, 2) and (5, 4).

Solution:

Let us considered P(-1, 2) and Q(5, 4) are the given point

So, the equation of line PQ is 

y – y₁ = m(x – x₁)

3y – x = 7                ……..(1)

And the slope of line PQ = 1/3

Let us considered point A(1, 0) is the given point and B(x₁, y₁) be the projection of A

So, the slope of AB = -3          

The equation of PQ is

y – 0 = -3(x – 1)

y = -3x + 3                  …….(2)

On solving eq(1) and (2), we get

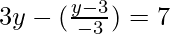
-9y – y + 3 = -21

-10y = -24

y = 12/5

12/5 = -3x + 3

-3x = 12/5 – 3 = (12 -15)/5 = -3/5

x = 1/5

Hence, the B(1/5, 12/5)

Question 23. Find the equation of a line perpendicular to the line √3x – y + 5 = 0 and at a distance of 3 units from the origin.

Solution:

Let us considered the required equation of line is 

y – y₁ = m'(x – x₁)      ……….(1)

It is given that the required line is perpendicular to the line √3x – y + 5 = 0 

So, the slope of the line is

y = √3x + 5

On comparing y = mx + c, we get

m = √3

m’ = -1/m = -1/√3

and the point is (x₁, y₁) = (3, 3)

Now put the value of m’ and (x₁, y₁) is eq(1), we get

y – 3 = -1/√3(x – 3)  

x + √3y – 6 = 0

Hence, the required equation of line is x + √3y – 6 = 0

Question 24. The line 2x + 3y = 12 meets the x-axis at A and y-axis at B. The line through (5, 5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB.

Solution:

It is given that the line 2x+3y=12 meets the x-axis at A and y-axis at B

So, A is 2x = 12 = x = 6

A is (6, 0)

B is 3y = 12

y = 4

B is (0, 4)

It is given that line through (5, 5) perpendicular to 2x + 3y = 12 will have slope = 3/2

y – y₁ = m(x – x₁)

(y – 5) = 3/2(x – 5)

And 2y – 3x = -5 is equation of line which meets x-axis at C and the line at E

So, C is -3x = -5

x = -5/3

E is (5/3, 0)

Here, E is the point of intersection of two lines

So, 2x + 3y = 12

2y – 3x = -5

Now we find the area of OBCE = area of AOB – area of ACE

= 1/2 x AO x OB – 1/2 x AC x CE

= 24/2 – 1/2 x √13 x 2/3√13

= 24/2 – 1/2 x 2/3 x 13

= 12 – 13/3

= 23/3 sq.unit

Question 25. Find the equation of the straight line which cuts of intercepts on x-axis twice that on y-axis and is at unit distance from the origin.

Solution:

Let us considered the equation of line in intercept form is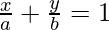 

It is given that its intercept on y-axis = 2a       

So, the equation is

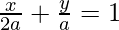
ax + 2ay = 2a²               ……..(1)

Now, perpendicular distance of eq(1) from origin is given unity 

So,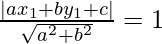 

a = a, b = 2a, c = -2a², x₁ = 0, y₁ = 0

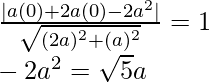
4a⁴ = a²5

a² = 5/4

a = ±√5/4

So, the intercept form of straight line is 

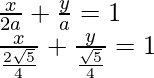
x + 2y = ±√5 

Hence, the required equation of line is x + 2y = ±√5 

Question 26. The equations of the perpendicular bisector of the sides AB and AC of a triangle ABC x – y + 5 = 0 and x + 2y = 0 respectively. If point A is (1, -2), find the equation of the line BC.

Solution:

Let us considered (x1, y1) and (x2, y2) be the coordinates of B and C.

It is given that perpendicular bisector of AB is x – y + 5 = 0

So, its slope = 1

The coordinates of F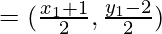

From the figure it is given that F lie on the x – y + 5 = 0

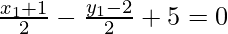
x₁ + 1 – y₁ + 2 + 10 = 0

x₁ – y₁ + 13 = 0               ……(1)

From the figure it is given that AB is perpendicular to HF

So, (slope of AB) x (slope of HF) = -1

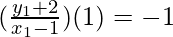
x₁ + y₁ + 1 = 0

Now on solving equation (1) and (2), we get

x₁ = -7,  y₁ = 6

So, B is (-7, 6)

Now, perpendicular bisector of AC is  x + 2y = 0

So, its slope = -1/2

The coordinate of E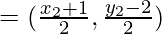 

From the figure it is given that E lies on perpendicular bisector of AC

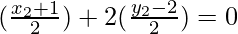
x₂ + 1 + 2y₂ – 4 = 0

x₂ + 2y₂ – 3 = 0              ……(3)

Also, AC is perpendicular to HE

So, (slope of AC) x (slope of HE) = -1

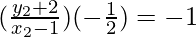
y₂ + 2 = 2x₂ – 2

2x₂ – y₂ = 4                …..(4)

On solving equation (3) and (4), we get

x₂ = 11/5 , y₂ = 2/5

Thus, point C is (11/5, 2/5) 

So, the equation of BC is 

y – y₁=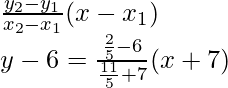

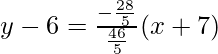
y – 6 = -14/23(x + 7)

23y – 138 = -14x – 98

14x + 23y – 40 = 0

Hence, the required equation of line is 14x + 23y – 40 = 0

Question 27. Find the equation of the straight line passing through the point of intersection of the lines 5x – 6y -1 = 0 and perpendicular to the line 3x – 5y + 11 = 0.

Solution:

Let us considered M be the point of intersection of the given lines 5x – 6y – 1 = 0 and 3x + 2y + 5 = 0

On solving both the equations we get the point of intersection as M (-1, -1).

Now we find the slope of 3x – 5y + 11 = 0

5y = 3x + 11

y = 3x/5 + 11/5

On comparing y = mx + c, we get

m = 3/5

From the figure we can see that AP is perpendicular to line 3x – 5y + 11 = 0

So, the slope of AP = -5/3

Now the equation of AP is 

y – y₁ = m(x – x₁)

y + 1 = -5/3(x + 1)

3y + 3 = -5x – 5

5x + 3y + 8 = 0

Hence, the equation of the line AP is 5x + 3y + 8 = 0