Question 1. Show that the lines 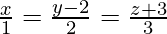 and
and 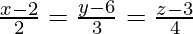 intersect and find their point of intersection.
intersect and find their point of intersection.
Solution:
Given that the coordinates of any point on the first line are
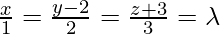
⇒ x = λ, y = 2λ + 2, z = 3λ – 3
The coordinates of a general point on the second line are given by:
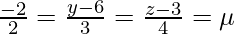
⇒ x = 2μ + 2, y = 3μ + 6, z = 4μ + 3
If the lines intersect, for some values of λ and μ, we must have:
λ – 2μ = 2 ……(1)
2λ – 3μ = 4 ……(2)
3λ – 4μ = 6 …..(3)
Solving this system of equations, we get
λ = 2 and μ = 0
On substituting the values in eq(3), we have
LHS = 3(2) – 4(0)
= 6 = RHS
Thus, the given lines intersect at (2, 6, 3).
Question 2. Show that the lines 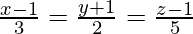 and
and 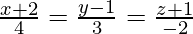 do not intersect.
do not intersect.
Solution:
Given that the coordinates of any point on the first line are
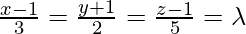
⇒ x = 3λ + 1, y = 2λ – 1, z = 5λ + 1
The coordinates of a general point on the second line are given by:
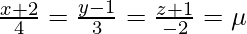
⇒ x = 4μ – 2, y = 3μ + 1, z = -2μ – 1
If the lines intersect, for some values of λ and μ, we must have:
3λ – 4μ = -3 ……(1)
2λ – 3μ = 2 ……(2)
5λ + 2μ = -2 …..(3)
Solving this system of equations, we get
λ = -17 and μ = -12
On substituting the values in eq(3), we have
LHS = 3(-17) + 2(-12)
= -75 ≠ RHS
Thus, the given lines do not intersect with each other.
Question 3. Show that the lines  and
and 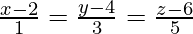 intersect and find their point of intersection.
intersect and find their point of intersection.
Solution:
Given that the coordinates of any point on the first line are
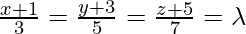
⇒ x = 3λ – 1, y = 5λ – 3, z = 7λ – 5
The coordinates of a general point on the second line are given by:
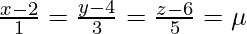
⇒ x = 2μ + 2, y = 3μ + 6, z = 4μ + 3
If the lines intersect, for some values of λ and μ, we must have:
3λ – μ = 3 ……(1)
5λ – 3μ = 7 ……(2)
7λ – 5μ = 11 …..(3)
Solving this system of equations, we get
λ = 1/2 and μ = -3/2
On substituting the values in eq(3), we have
LHS = 3(2) – 4(0)
= -3/2 = RHS
Now put the value of λ in first equation and we get
x = 1/2, y = -1/2, z = -3/2
Thus, the given lines intersect at (1/2, -1/2, -3/2).
Question 4. Prove that the line through (0, -1, -1) and B(4, 5, 1) intersects the line through C(3, 9, 4) and D(-4, 4, 4). Also, find their point of intersection.
Solution:
Given that the coordinates of any point on the line AB are
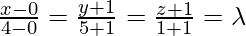
⇒ x = 4λ, y = 6λ – 1, z = 2λ – 1
Also, given that the coordinates of any point on the line CD are
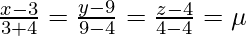
⇒ x = 7μ + 3, y = 5μ + 9, z = 4
If the lines intersect, for some values of λ and μ, we must have:
4λ – 7μ = 3 ……(1)
6λ – 5μ = 10 ……(2)
λ = 5/2 …..(3)
⇒ λ = 5/2 and μ = 1.
On substituting the values in eq(3), we have
LHS = 4(5/2) – 7(1)
= 3 = RHS
Now put the value of λ in line AB, we get
x = 10, y = 14, z = 4
Thus, the given lines AB and CD intersect at point (10, 14, 4).
Question 5. Prove that the line 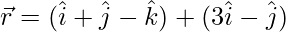 and
and 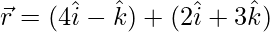 intersect and find their point of intersection.
intersect and find their point of intersection.
Solution:
According to the question, it is given that the position vector of two points on the lines are
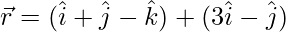
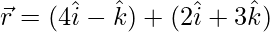
If the lines intersect, then for some value of λ and μ, we must have:
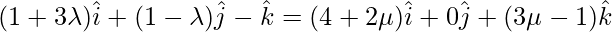
Now equate the coefficient of 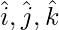 we get
we get
1 + 3λ = 4 + 2μ ……(1)
1 – λ = 0 …..(2)
-1 = -1 +3μ …..(3)
On solving the equation, we get
λ = 1 and μ = 0.
Now, substituting the values in eq(1), we get
1 + 3(1) = 4 + 2(0)
4 = 4
LHS = RHS
Thus, the coordinates of the point of intersection of the two lines are (4, 0, -1).
Question 6. Determine whether the following pairs of lines intersect or not:
(i) 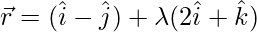 and
and 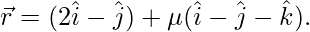
Solution:
Given that:
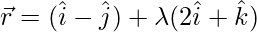
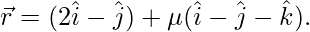
If the lines intersect, then for some value of λ and μ, we must have:
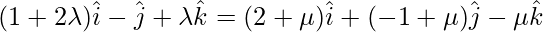
Now equate the coefficient of 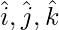 we get
we get
1 + 2λ = 2 + μ …..(1)
-1 = -1 + μ …..(2)
λ = -μ …..(3)
On solving the equations, we get
λ = 0 and μ = 0.
Now, substitute the values in eq(1), we get
1 + 2λ = 2 + μ
1 + 2(0) = 2 + 0
1 ≠ 2
LHS ≠ RHS
Thus, the given lines do not intersect.
(ii) 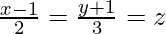 and
and 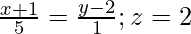
Solution:
Given that the coordinates of any point on the line AB are
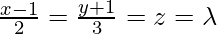
⇒ x = 2λ + 1, y = 3λ – 1, z = λ
The coordinates of a general point on the second line are given by
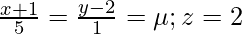
⇒ x = 5μ – 1, y = μ + 2, z = 2
If the lines intersect, for some values of λ and μ, we must have:
2λ – 5μ = -2 ……(1)
3λ – μ = 3 ……(2)
λ = 2 …..(3)
Solving this system of equations, we get
λ = 2 and μ = 3
On substituting the values in eq(3), we have
LHS = 2(2) – 5(3)
= -2 ≠ RHS
Thus, the given lines do not intersect each other.
(iii) 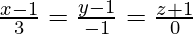 and
and 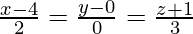
Solution:
Given that the coordinates of any point on the line AB are
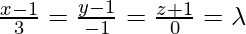
⇒ x = λ, y = 2λ + 2, z = 3λ – 3
The coordinates of a general point on the second line are given by
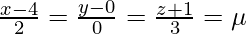
⇒ x = 2μ + 4, y = 0, z = 3μ – 1
If the lines intersect, for some values of λ and μ, we must have:
λ – 2μ = 2 …….(1)
2λ – 3μ = 4 ……(2)
3λ – 4μ = 6 ……(3)
On solving this system of equations, we get
λ = 1 and μ = 0
On substituting the values in eq(3), we have
LHS = 3(1) – 2(0)
= 3 = RHS
Thus, the given lines intersect at (4, 0, -1).
(iv) 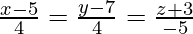 and
and 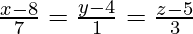
Solution:
Given that the coordinates of any point on the line AB are
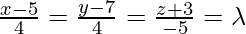
⇒ x = 4λ + 5, y = 4λ + 7, z = -5λ – 3
The coordinates of a general point on the second line are given by:
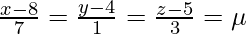
⇒ x = 7μ + 8, y = μ + 4, z = 3μ + 5
If the lines intersect, for some values of λ and μ, we must have:
4λ – 7μ = 3 …….(1)
4λ – μ = -3 ……(2)
5λ + 3μ = -8 ……(3)
On solving this system of equations, we get
λ = -1 and μ = -1
On substituting the values in eq(3), we have
LHS = 5(-1) – 3(-1)
= -8 = RHS
Thus, the given lines intersect at (1, 3, 2).
Question 7. Show that the lines 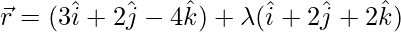 and
and 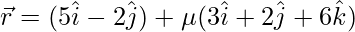 are intersecting. Hence, find their point of intersection.
are intersecting. Hence, find their point of intersection.
Solution:
Given that,
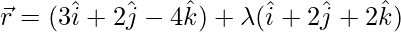
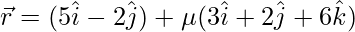
If the lines intersect, then for some value of λ and μ, we must have:
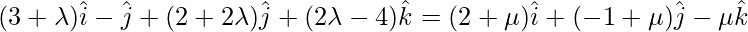
Now equate the coefficient of  we get
we get
3 + λ = 5 + 3μ ……..(1)
2 + 2λ = -2 + 2μ ……..(2)
2λ – 4 = 6μ ……..(3)
Solving the equation, we have:
λ = -4 and μ = -2.
On substituting the values, we get
LHS = 2(-4) – 4
= -12
RHS = 6(-2)
= -12
Thus, the given lines intersect at point(-1, -6, -12).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...