Class 12 RD Sharma Solutions – Chapter 28 The Straight Line in Space – Exercise 28.1 | Set 2
Last Updated :
04 May, 2021
Question 11. Find the direction cosines of the line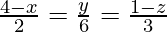 . Also, reduce it to vector form
. Also, reduce it to vector form
Solution:
Given:
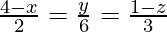
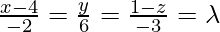
x = -2λ + 4, y = 6λ, z = -3λ + 1
So,
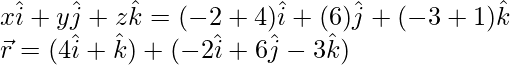
Direction ratios of the line are = -2, 6, -3
Direction cosines of the lines are,
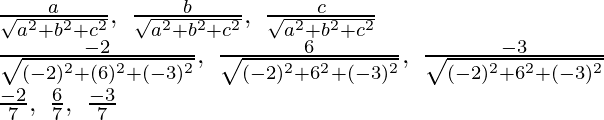
Question 12. The Cartesian equations of a line are x = ay + b, z = cy + d. Find its direction ratios and reduce it to vector form.
Solution:
x = ay + b
z = cy + d
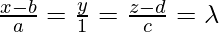
So, DR’s of line are (a, 1, c)
From above equation, we can write
x = aλ + b
y = λ
z = cλ + d
So vector equation of line is
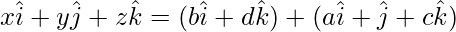
Question 13. Find the vector equation of a line passing through the point with position vector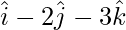 and parallel to the line joining the points with the position vector
and parallel to the line joining the points with the position vector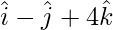 and
and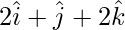 . Also, find the Cartesian equivalent of this equation.
. Also, find the Cartesian equivalent of this equation.
Solution:
We know that, equation of a line passing through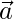 and parallel to vector
and parallel to vector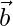 is
is
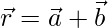 ……. (i)
……. (i)
Here,
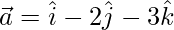
and, \vec{b} = line joining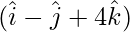 and
and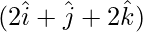
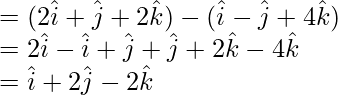
Equation of the line is
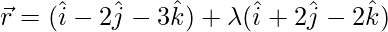
For Cartesian form of equation put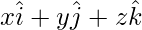
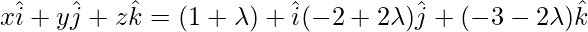
Equating coefficients of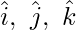
x = 1 + λ, y = -2 + 2λ, z = -3 – 2λ
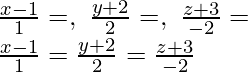
Question 14. Find the points on the line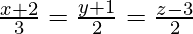 at a distance of 5 units from the points P(1, 3, 3).
at a distance of 5 units from the points P(1, 3, 3).
Solution:
Given, line is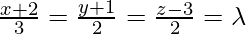
General points Q on line is (3λ – 2, 2λ -1), 2λ + 3)
Distance of points P from Q =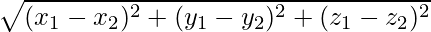
PQ =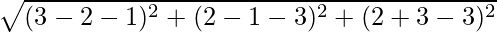
(5)2 = (3λ -3)2 + (2λ – 4) + (2λ)2
25 = 9λ2 + 9 – 18λ + 4λ2 + 16 – 16λ + 4λ2
17λ2 – 34λ = 0
17λ (λ – 2) = 0
λ = 0 or 2
So, points on the line are (3(0) – 2, 2(0) – 1, 2(0) + 3)
(3(2) – 2, 2(2) – 1, 2(2) + 3)
= (-2, -1, 3), (4, 3, 7)
Question 15. Show that the points whose position vectors are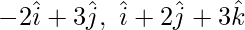 and
and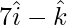 are collinear.
are collinear.
Solution:
Let the given points are A,B.C with position vectors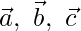 respectively.
respectively.
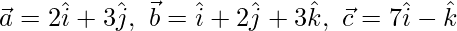
We know that, equation of a line passing through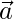 and
and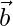 are
are
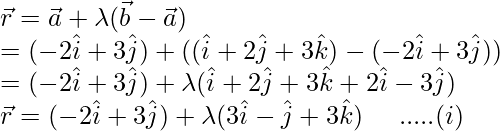
If A, B, C are collinear then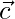 must satisfy equation (i)
must satisfy equation (i)
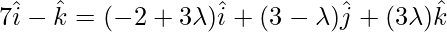
Equation the coefficients of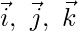
-2 + 3 = 7 , λ = 3
3 – λ = 0 , λ = 3
3λ = -1 , λ =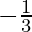
Since, value of λ are not equal, so,
Given points are collinear.
Question 16. Find the Cartesian and vector equations of a line which passes through the points (1, 2, 3) and is parallel to the line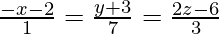
Solution:
We know that, equation of a line passing through a point (x1, y1, z1) and having direction ratios proportional to a, b, c is
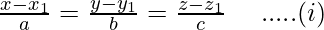
Here,
(x1, y1, z1) = (1, 2, 3) and
Given line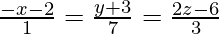
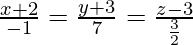
Its parallel to the required line, so
a = μ , b = 7μ, c =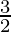 μ
μ
So, equation of required line using equation (i) is,
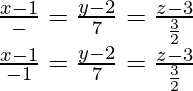
Multiplying the denominators by 2
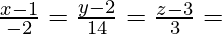
x = -2λ + 1, y = 14λ + 2, z = 3λ + 3
So, vector form of the equation of required line,
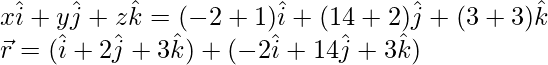
Question 17. The Cartesian equations of a line are 3x + 1 = 6y – 2 = 1 – z. Find the fixed point through which it passes, its direction ratios, and also its vector equation.
Solution:
Given equation of line is,
3x + 1 = 6y -2 = 1 – z
Dividing all by 6
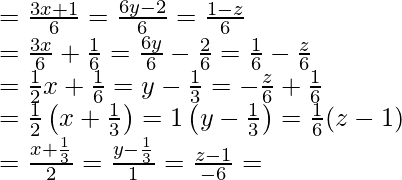
Comparing it with equation of line equation of line passing through (x,1 y1, z1) and the direction ratios a, b, c,
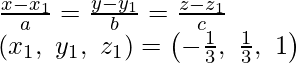
a = 2, b = 1, -6
So, direction ratios of the line are -2, 1, -6
From equation (i)
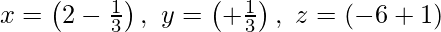
So, vector equation of the given line is,
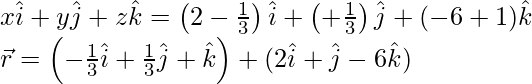
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...