Class 12 RD Sharma Solutions- Chapter 13 Derivative as a Rate Measurer – Exercise 13.2 | Set 1
Last Updated :
28 Jan, 2021
Question 1. The side of a square sheet is increasing at the rate of 4 cm per minute. At what rate is the area increasing when the side is 8 cm long?
Solution:
Let the side of the square sheet be denoted by ‘a’, then area (A) of the sheet will be a2 cm2.
It is given that side is increasing at the rate of 4cm/min, i.e.,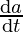 = 4cm/min
= 4cm/min
Since, A = a2
⇒ = 2a
= 2a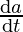
⇒ = 2 x 8 x 4 [ Since, a=8 and
= 2 x 8 x 4 [ Since, a=8 and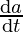 = 4cm/min]
= 4cm/min]
⇒ = 64 cm2/min
= 64 cm2/min
Question 2. An edge of a variable cube is increasing at the rate of 3 cm per second. How fast is the volume of the cube increasing when the edge is 10 cm long?
Solution:
Let the edge of the cube be denoted by symbol ‘a’ and volume of the cube be denoted by ‘V’.
Now, as given the edge of variable cube is increasing, i.e.,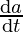 = 3 cm/sec
= 3 cm/sec
Since, V = a3
⇒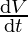 = 3a2
= 3a2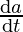
⇒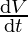 = 3 x 10 x 10 x 3 [Since, a=10 and
= 3 x 10 x 10 x 3 [Since, a=10 and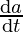 = 3 cm/sec]
= 3 cm/sec]
⇒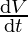 = 900 cm3/sec
= 900 cm3/sec
Question 3. The side of a square is increasing at the rate of 0.2 cm/sec. Find the rate of increase of the perimeter of the square.
Solution:
Let the side of the square be denoted by a cm and its perimeter (P) = 4a cm
As given, the side is increasing, i.e.,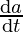 = 0.2 cm/sec
= 0.2 cm/sec
Now since, P = 4a
⇒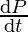 = 4
= 4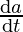
⇒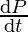 = 4 x 0.2
= 4 x 0.2
⇒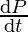 = 0. 8 cm/sec
= 0. 8 cm/sec
Question 4. The radius of a circle is increasing at the rate of 0.7 cm/sec. What is the rate of increase of its circumference?
Solution:
Let the radius of the circle be denoted by ‘r’ cm and its circumference is given by C = 2*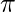 *r
*r
Also given, the radius is increasing i.e.,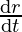 = 0.7 cm/sec at any time t.
= 0.7 cm/sec at any time t.
Rate of increase of its circumference =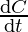
⇒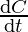 = 2*
= 2*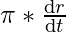
⇒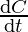 = 2 * 22/7 * 0.7
= 2 * 22/7 * 0.7
⇒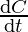 = 4.4 cm/sec
= 4.4 cm/sec
Question 5. The radius of a spherical soap bubble is increasing at the rate of 0.2 cm/sec. Find the rate of increase of its surface area, when the radius is 7 cm.
Solution:
Let the radius of the spherical soap be denoted by ‘r’ and its surface area (S) = 4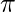 r2
r2
Also, given the radius is increasing i.e.,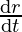 = 0.2 cm/sec
= 0.2 cm/sec
Therefore, the increase of surface area at any time t is given by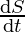
⇒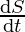 = 4*
= 4*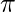 *2r*
*2r*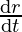
⇒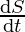 = 8 * 22/7 * 7 * 0.2
= 8 * 22/7 * 7 * 0.2
⇒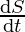 = 35.2 cm2/sec
= 35.2 cm2/sec
Question 6. A balloon which always remains spherical, is being inflated by pumping in 900 cubic centimetres of gas per second. Find the rate at which the radius of the balloon is increasing when the radius is 15 cm.
Solution:
Let the radius of the spherical balloon be denoted by ‘r’ and volume being inflated at \frac{\mathrm{d} V}{\mathrm{d} t} = 900 cm3/sec
Since, V =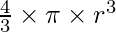
⇒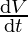 =
=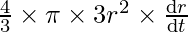
⇒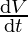 =
=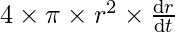
⇒ 900 = 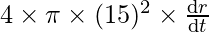
⇒ 900 =900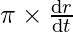
⇒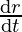 =
=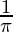 cm/sec.
cm/sec.
Question 7. The radius of an air bubble is increasing at the rate of 0.5 cm/sec. At what rate is the volume of the bubble increasing when the radius is 1 cm?
Solution:
Let the radius of the bubble be denoted by ‘r’ and its volume be denoted by V where V =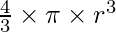
Now at any time t, radius is increasing i.e.,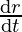 = 0.5 cm.sec
= 0.5 cm.sec
Therefore, = 4
= 4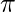 *r2*
*r2*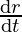
⇒ = 4
= 4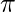 * (1)2 * 0.5
* (1)2 * 0.5
⇒ = 2
= 2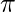 cm3/sec
cm3/sec
Question 8. A man 2 metres high walks at a uniform speed of 5 km/hr away from a lamp-post 6 metres high. Find the rate at which the length of his shadow increases.
Solution:
Let MN denote the vertical lamp post of height 6 meter and at any instant t, a man XY of height 2 meter be standing in front of the lamp post at a distance ‘m’ and let ‘n’ be length of his shadow. It can be seen in a figure as:

We can notice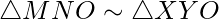
⇒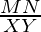 =
=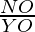
⇒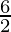 =
=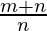
⇒ 3n = m + n
⇒ m = 2n
⇒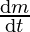 = 2
= 2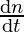
⇒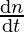 =
=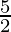 km/hr
km/hr
Question 9. A stone is dropped into a quiet lake and waves move in circles at a speed of 4 cm/sec. At the instant when the radius of the circular wave is 10 cm, how fast is the enclosed area increasing?
Solution:
Let the radius of circular wave be denoted by ‘r’ and at any instant t, its radius increasing at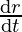 = 4 cm/sec
= 4 cm/sec
Now, area of circular wave (A) =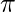 r2
r2
⇒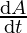 = 2
= 2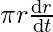
⇒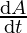 = 2*
= 2*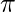 *10* 4
*10* 4
⇒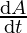 = 80
= 80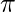 cm2/sec
cm2/sec
Question 10. A man 160 cm tall, walks away from a source of light situated at the top of a pole 6 m high, at the rate of 1.1 m/sec. How fast is the length of his shadow increasing when he is 1 m away from the pole?
Solution:
Let the vertical pole of light be denoted by MN and the man be denoted by XY, then his position with respect to lamp can be drawn as shown in figure:

We can notice,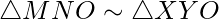
⇒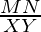 =
=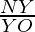
⇒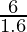 =
=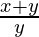
⇒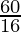 =
=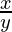 + 1
+ 1
⇒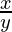 =
=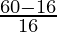
⇒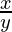 =
=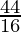
⇒ y =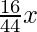
⇒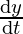 =
=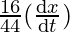
⇒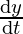 =
=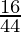 * 1.1
* 1.1
⇒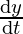 = 0.4 m/sec
= 0.4 m/sec
Question 11. A man 180 cm tall walks at a rate of 2 m/sec. away, from a source of light that is 9 m above the ground. How fast is the length of his shadow increasing when he is 3 m away from the base of light?
Solution:
Let MN denote the vertical lamp post of height 6 meter and at any instant t, a man XY of height 2 meter be standing in front of the lamp post at a distance ‘m’ and let ‘n’ be length of his shadow. It can be seen in a figure as:

We can notice
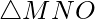 ∼
∼ 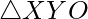
⇒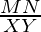 =
=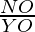
⇒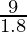 =
= 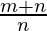
⇒ m = 4n
⇒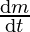 = 4
= 4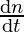
⇒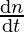 =
=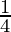 x 2 [Since,
x 2 [Since,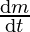 = 2]
= 2]
⇒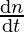 = 0.5 m/sec
= 0.5 m/sec
Question 12. A ladder 13 m long leans against a wall. The foot of the ladder is pulled along the ground away from the wall, at the rate of 1.5 m/sec. How fast is the angle θ between the ladder and the ground is changing when the foot of the ladder is 12 m away from the wall.
Solution:
Let the height of the wall that is leaning against a wall be denoted by y meters and the distance of the foot of ladder from base of the wall be x meters.
we can derive tan θ = y/x ⇒ y = xtan θ
Also, using Pythagoras theorem, x2 + y2 = (13)2
⇒ x2 + (xtan θ )2 = 169
⇒ x2 (1+tan2 θ ) = 169
⇒ sec2 θ = 169/x2
⇒ 2 sec θ . tan θ sec θ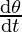 = 169.
= 169.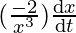
⇒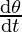 =
=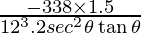 ………………(1)
………………(1)
Using Pythagoras Theorem, when x=12, then y=5
Therefore, sec θ = 13/12 and tan θ = 12/5
Then, equation 1 can be written as
⇒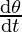 =
=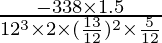
⇒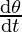 = -0.3 rad/sec
= -0.3 rad/sec
Question 13. A particle moves along the curve y = x2+ 2x. At what point(s) on the curve are the x and y coordinates of the particle changing at the same rate?
Solution:
We are given y = x2 + 2x
⇒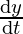 = 2x
= 2x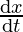 + 2
+ 2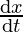
⇒ 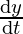 = (2x+2)
= (2x+2)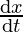
⇒ 2x + 2 = 1 [Since,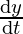 =
=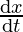 ]
]
⇒ x = -1/2
Putting the value of x in our original equation, we get y= -3/4
Hence, the coordinates of the point are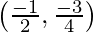
Question 14. If y = 7x – x3 and x increases at the rate of 4 units per second, how fast is the slope of the curve changing when x = 2?
Solution:
We are given y = 7x – x3
⇒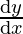 = 7 – 3x2
= 7 – 3x2
Let the slope of the curve be denoted by m, then
⇒ m = 7 – 3x2
⇒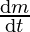 = -6x
= -6x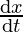
⇒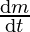 = -6 x 4 x 2
= -6 x 4 x 2
⇒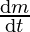 = -48
= -48
Therefore, the slope of the curve is decreasing at the rate of 48 units/sec.
Question 15. A particle moves along the curve y = x3. Find the points on the curve at which the y-coordinate changes three times more rapidly than the x-coordinate.
Solution:
We are given y = x3
⇒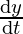 = 3x2
= 3x2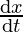
Also, the point on y-coordinate changes 3 times more rapidly than x-coordinate, therefore
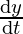 = 3
= 3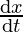
⇒ 3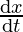 = 3x2
= 3x2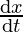
⇒ x2 = 1
⇒ x = ±1
Substituting the value of x in y = x3, we get y = ±1
So, the points are (1,1) and (-1,-1).
Question 16 (i) Find an angle θ which increases twice as fast as its cosine?
(ii) Find an angle θ whose rate of increase twice is twice the rate of decrease of its cosine?
Solution:
(i) Let x = cos∅
Differentiating both sides with respect to t, we get
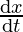 = -sin∅
= -sin∅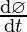
According to the condition given in question:
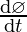 = 2
= 2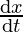
⇒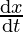 = -sin∅
= -sin∅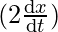
⇒ sin∅ = -1/2
⇒ ∅ = π + π/6 = 7π/6
(ii) Let x = cos∅
Differentiating both sides with respect to t, we get
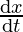 = -sin∅
= -sin∅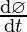
According to the condition given in question:
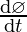 = -2
= -2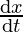
⇒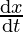 = -sin∅
= -sin∅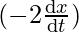
⇒ sin∅ = 1/2
Share your thoughts in the comments
Please Login to comment...