Class 12 RD Sharma Solutions – Chapter 31 Probability – Exercise 31.7 | Set 3
Last Updated :
07 Nov, 2022
Question 27. There are three coins. One is a two-headed coin, another is a biased coin that comes up heads 75% of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads. What is the probability that it was the two-headed coin?
Solution:
Let us assume that the events are
E1 = choosing a two-headed coin
E2 = choosing a biased coin
E3 = choosing an unbiased coin
A = the coin shows heads.
So,
P(E1) = 1/3
P(E2) = 1/3
P(E3) = 1/3
Now,
P(A/E1) = 1
P(A/E2) = 75% = 3/4
P(A/E3) = 1/2
By using Bayes’ theorem, the required probability is
P(E1/A) = 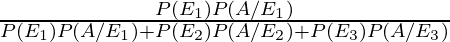
= 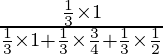
= 4/9
Question 28. Assume that the chances of a patient having a heart attack is 40%. It is also assumed that meditation and yoga course reduces the risk of heart attack by 30% and prescription of certain drug reduces its chances by 25%. At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options and patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga?
Solution:
Let us assume that the events are
E1 = follow the course of yoga and meditation
E2 = follow the drug prescriptions
A = the selected person had heart attack
So,
P(E1) = 1/2
P(E2) = 1/2
Now,
P(A/E1) = 0.4 x 0.70 = 0.28
P(A/E2) = 0.4 x 0.75 = 0.30
By using Bayes’ theorem, the required probability is
P(E1/A) = 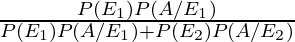
= 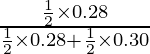
= 14/29
Question 29. Colored balls are distributed in four boxes as shown in the following table:
Box
| Colour
|
| Black
| White
| Red
| Blue
|
I
| 3
| 4
| 5
| 6
|
II
| 2
| 2
| 2
| 2
|
III
| 1
| 2
| 3
| 1
|
IV
| 4
| 3
| 1
| 5
|
A box is selected at random and then a ball is randomly drawn from the selected box. The color of the ball is black, what is the probability that the ball drawn is from box III.
Solution:
Let us assume that the events are
A = the ball is black
E1 = box I selected
E2 = box II selected
E3 = box III is selected
E4 = box IV is selected
So,
P(E1) = 1/4
P(E2) = 1/4
P(E3) = 1/4
P(E4) = 1/4
Now,
P(A/E1) = 3/18
P(A/E2) = 2/8
P(A/E3) = 1/7
P(A/E4) = 4/13
By using Bayes’ theorem, the required probability is
P(E3/A) = 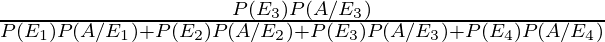
= 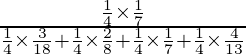
= 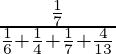
= 156/947
Question 30. If a machine is correctly set up it produces 90% acceptable items. If it is incorrectly set up it produces only 40% acceptable item. Past experience shows that 80% of the setups are correctly done. If after a certain setup, the machine produces 2 acceptable items, find the probability that the machine is correctly set up.
Solution:
Let us assume that the events are
A = the machine produces two acceptable items.
E1 = the machine is correctly set up
E2 = the machine is incorrectly set up
So,
P(E1) = 0.8
P(E2) = 0.2
Now,
P(A/E1) = 0.9 (0.9) = 0.81
P(A/E2) = 0.40 (0.40) = 0.16
By using Bayes’ theorem, the required probability is
P(E1/A) = 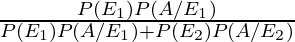
= 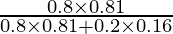
= 81/85
Question 31. Bag A contains 3 red and 5 black balls, while bag B contains 4 red and 4 black balls. Two balls are transferred at random from bag A to bag B and then a ball is drawn from bag B at random. If the ball drawn from bag B is found to be red find the probability that two red balls were transferred from A to B.
Solution:
According to the question, bag A contains 3 red and 5 black balls and bag B contains 4 red and 4 black balls.
Let us assume that the events are
E1 = Two red balls are transferred from bag A to bag B.
E2 = One red ball and one black ball is transferred from bag A to bag B.
E3 = Two black balls are transferred from bag A to bag B.
A = Ball drawn from bag B is red.
So,
P(E1) = 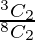 = 3/28
= 3/28
P(E2) = 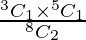 = 15/28
= 15/28
P(E3) = 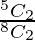 = 10/28
= 10/28
Also,
P(A/E1) = 6/10
P(A/E2) = 5/10
P(A/E3) = 4/10
P(E1/A) is the required probability, that two red balls were transferred from A to B given that the ball drawn from bag B is red
So, by using Bayes’ theorem, the required probability is
= 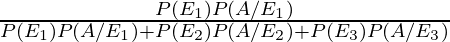
= 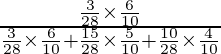
= 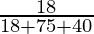
= 18/133
Question 32. Let d1, d2, d3 be three mutually exclusive diseases. Let S be the set of observable symptoms of these diseases. A doctor has the following information from a random sample of 5000 patients: 1800 had disease d1, 2100 has disease d2 and the others had disease d3. 1500 patients with disease d1, 1200 patients with disease d2 and 900 patients with disease d3 showed the symptoms. Which of the diseases is the patient most likely to have?
Solution:
Let us assume that the events are
A = the patient shows symptoms S
E1 = has disease d1
E2 = has disease d2
E3 = has disease d3
So,
P(E1) = 1800/5000
P(E2) = 2100/5000
P(E3) = 1100/5000
Now,
P(A/E1) =1500/1800
P(A/E2) = 1200/2100
P(A/E3) = 900/1100
By using Bayes’ theorem, the required probabilities are
P(E1/A) = 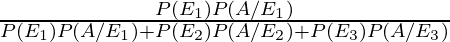
= 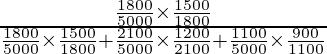
= 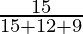
= 15/36
= 5/12
P(E2/A) = 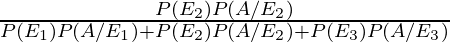
= 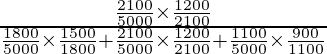
= 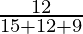
= 12/36
= 1/3
P(E3/A) = 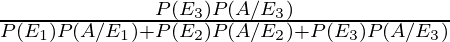
= 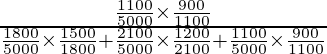
= 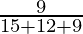
= 9/36
= 1/4
As P(E1/A ) is maximum, so it is most likely that the person have d1 disease.
Question 33. A test for the detection of a particular disease is not foolproof. The test will correctly detect the disease 90% of the time, but will incorrectly detect the disease 1% of the time. For a large population of which an estimated 0.2% have the disease, a person is selected at random, given the test, and told that he has the disease. What are the chances that the person actually has the disease?
Solution:
Let us assume that the events are
A = the person suffers from the disease
E1 = the test detects the disease correctly
E2 = the test does not detect the disease correctly
So,
P(E1) = 90/100
P(E2) = 1/100
Now,
P(A/E1) = 2/1000
P(A/E2) = 998/1000
By using Bayes’ theorem, the required probability is
P(E1/A) = 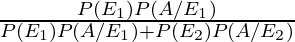
= 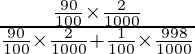
= 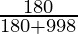
= 180/1178
= 90/589
Question 34. Let d1, d2, d3, d4 be three mutually exclusive diseases. Let S be the set of observable symptoms of these diseases. A doctor has the following information from a random sample of 5000 patients: 1800 had disease d1, 2100 has disease d2, and others had disease d3. 1500 patients with disease d1, 1200 patients with disease d2, and 900 patients with disease d3 showed the symptoms. Which of the diseases is the patient most likely to have?
Solution:
Let us assume that the events are
E1 = The patient had disease d1
E2 = The patient had disease d2
E3 = The patient had disease d3
S = The patient showed the symptom
Also, E1, E2, and E3 are mutually exclusive and exhaustive events.
So,
P(E1) = 1800/1500 = 18/50
P(E2) = 2100/5000 = 21/50
P(E3) = 1100/5000 = 11/50
Now,
P(S/E1) = The probability that the patient had disease d1 and showed symptoms S = 1500/5000 = 15/50
P(S/E2) = The probability that the patient had disease d2 and showed symptoms S = 1200/5000 = 12/50
P(S/E3) = The probability that the patient had disease d3 and showed symptoms S = 900/5000 = 9/50
By using Bayes’ theorem,
P(E1/S) is the probability that patient had disease d1 such that symptoms of d1 appears
= 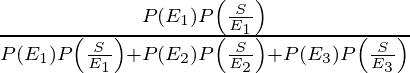
= 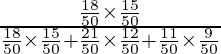
= 270/621
P(E2/S) is the probability that patient had disease d2 such that symptom of d2 appears
= 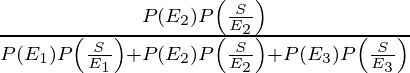
= 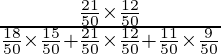
= 252/621
P(E3/S) is the probability that patient had disease d3 such that symptom of d3 appears
= 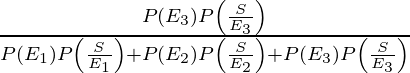
= 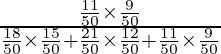
= 99/621
Hence, P(E1/A) is the maximum, then the patient is most likely to have the disease d1.
Question 35. A is known to speak the truth 3 times out of 5 times. He throws a die and reports that it is one. Find the probability that it is actually one.
Solution:
Let us assume that the events are
A = the man reports the appearance of 1 on throwing a die
E1 = 1 occurs
E2 = 1 does not occur
So,
P(E1) = 1/6
P(E2) = 5/6
Now,
P(A/E1) = 3/5
P(A/E2) = 2/5
By using Bayes’ theorem, the required probability is
P(E1/A) = 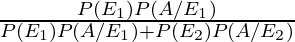
= 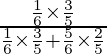
= 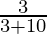
= 3/13
Question 36. A speaks the truth 8 times out of 10 times. A die is tossed. He reports that it was 5. What is the probability that it was actually 5?
Solution:
Let us assume that A be the event that man reports that 5 occurs and E the event that 5 actually turns up.
So,
P(E) = 1/6
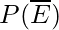 = 1 – 1/6 = 5/6
= 1 – 1/6 = 5/6
Also,
P(A/E) = Probability that man reports that 5 occurs given that 5 actually turns up
= Probability of man speaking the truth
= 8/10
= 4/5
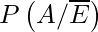 = Probability that man reports that 5 occurs given that 5 does not turns up
= Probability that man reports that 5 occurs given that 5 does not turns up
= Probability of man not speaking the truth
= 1 – 4/5
= 1/5
Therefore, the required probability = P(E/A)
= 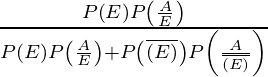
= 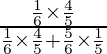
= 4/9
Question 37. In answering a question on a multiple-choice test a student either knows the answer or guesses. Let 3/4 be the probability that he knows the answer and 1/4 be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with a probability of 1/4. What is the probability that a student knows the answer given that he answered it correctly?
Solution:
Let us assume that the events are
A = the answer is correct
E1 = the student knows the answer
E2 = the student guesses the answer
So,
P(E1) = 3/4
P(E2) = 1/4
Now,
P(A/E1) = 1
P(A/E2) = 1/4
By using Bayes’ theorem, the required probability is
P(E1/A) = 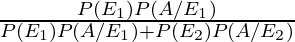
= 
= 3/3 + 1/4
= 12/13
Question 38. A laboratory blood test is 99% effective in detecting a certain disease when its infection is present. However, the test also yields a false positive result for 0.5% of the healthy person tested (i.e. if a healthy person is tested, then, with probability 0.005, the test will imply he has the disease). If 0.1% of the population actually has the disease, what is the probability that a person has the disease given that his test result is positive?
Solution:
Let us assume that E1 and E2 be the events that a person has a disease and a person has no disease.
Also, E1 and E2 are complimentary to each other.
So, P(E1) + P(E2) = 1
P(E1) = 0.001
=> P (E2) = 1 − P (E1) = 1 − 0.001 = 0.999
Let us assume that A be the event that the blood test result is positive.
Now,
P(A/E1) = 99% = 0.99
P(A/E2) = 0.5 % = 0.005
By using Bayes’ theorem, the required probability is
P(E1/A) = 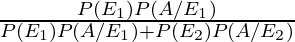
= 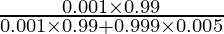
= 990/5985
= 22/133
Question 39. There are three categories of students in a class of 60 students:
A: Very hardworking; B: Regular but not so hardworking; C: Careless and irregular 10 students are in category A, 30 in category B, and the rest in category C. It is found that the probability of students of category A, unable to get good marks in the final year examination is 0.002, of category B it is 0.02 and of category C, this probability is 0.20. A student selected at random was found to be one who could not get good marks in the examination. Find the probability that this student is category C.
Solution:
Let us assume that the events are
E = the student could not get good marks in the examination.
A = student is very hardworking
B = student is regular but not so hardworking
C = student is careless and irregular
Here, we have
P(A) = 10/60
P(B) = 30/60
P(C) = 20/60
Also,
P(E/A) = Probability that category A student could not get good marks in the examination = 0.002
P(E/B) = Probability that a category B student could not get good marks in the examination = 0.02
P(E/C) = Probability that a category C student could not get good marks in the examination = 0.2
So, P(C/E) is the required probability
= 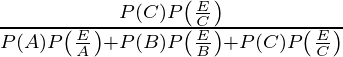
= 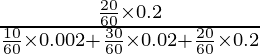
= 4/4.62
= 400/462
= 200/231
Share your thoughts in the comments
Please Login to comment...