Question 1. Show that Limx→0(x/|x|) does not exist.
Solution:
We have, Limx→0(x/|x|)
Now first we find left-hand limit:
= 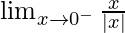
Let x = 0 – h, where h = 0
= 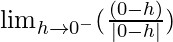
= 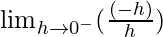
= -1
Now we find right-hand limit:
= 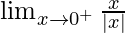
So, let x = 0 + h, where h = 0
= 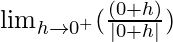
= 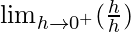
= 1
Left-hand limit ≠ Right-hand limit
So, Limx→0(x/|x|) does not exist.
Question 2. Find k so that Limx→0f(x), where 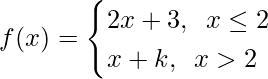
Solution:
We have, 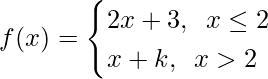
Now first we find left-hand limit:
= 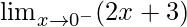
Let x = 2 – h, where h= 0.
=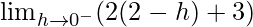
= [2(2 – 0) + 3]
= 7
Now we find right-hand limit:
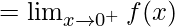
= 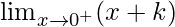
Let x = 2 + h, where h = 0
= 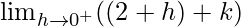
= (2 + 0) + k
= (2 + k)
Here, Left-hand limit = Right-hand limit, so limit exists
So, (2 + k) = 7
k = 5
Question 3. Show that Limx→0(1/x) does not exist.
Solution:
We have to show that Limx→0(1/x) does not exists
So for that
First we find left-hand limit:
= 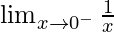
Let x = 0 – h, where h = 0.
= 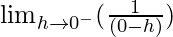
= 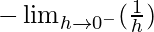
= -∞
Now we find right-hand limit:
=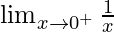
Let x = 0 + h, where h = 0.
= 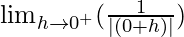
= 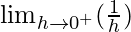
= ∞
Here, Left-hand limit ≠ Right-hand limit, so, Limx→0(1/x) does not exist.
Question 4. Let f(x) be a function defined by 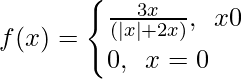 . Show that limx→0 f(x) does not exist.
. Show that limx→0 f(x) does not exist.
Solution:
We have, 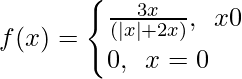
According to the question we have to show that limx→0 f(x) does not exist.
So for that
First we find left-hand limit:
=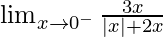
Let x = 0 – h, where h = 0
=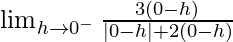
=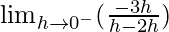
=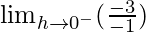
= 3
Now we find right-hand limit:
=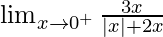
Let x = 0 + h, where h = 0.
=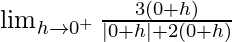
=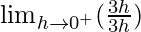
=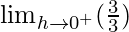
= 1
Here, Left-hand limit ≠ Right-hand limit, so, limx→0 f(x) does not exist.
Question 5. Let 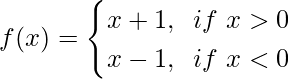 , Prove that limx→0f(x) does not exist.
, Prove that limx→0f(x) does not exist.
Solution:
We have, 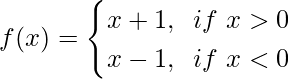
And we have to prove that limx→0f(x) does not exist.
So for that
First we find left-hand limit:
=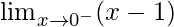
Let x = 0 – h, where h = 0.
=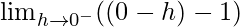
=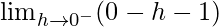
= -1
Now we find right-hand limit:
=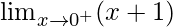
Let x = 0 + h, where h = 0.
=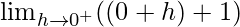
=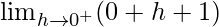
= 1
Here, Left-hand limit ≠ Right-hand limit, so, limx→0f(x) does not exist.
Question 6. Let 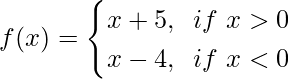 , Prove that limx→0f(x) does not exist.
, Prove that limx→0f(x) does not exist.
Solution:
We have,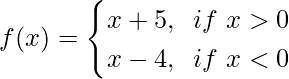
And we have to prove that limx→0f(x) does not exist.
So for that
First we find left-hand limit:
=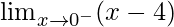
Let x = 0 – h, where h = 0.
=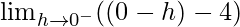
=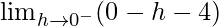
= -4
Now we find right-hand limit:
=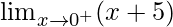
Let x = 0 + h, where h = 0.
=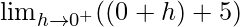
=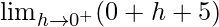
= 5
Here, Left-hand limit ≠ Right-hand limit, so, limx→0f(x) does not exist.
Question 7. Find limx→3f(x), where 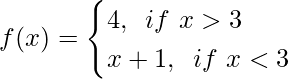
Solution:
We have, 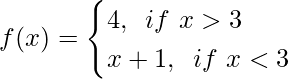
And we have to find limx→3f(x)
So for that
First we find left-hand limit:
=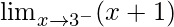
Let x = 3 – h, where h = 0.
= 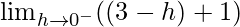
= 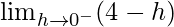
= 4
Now we find right-hand limit:
=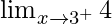
Let x = 3 + h, where h = 0.
=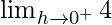
= 4
Here, Left-hand limit = Right-hand limit,
Hence, limx→3f(x) = 4
Question 8(i). If 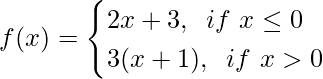 , Find limx→0f(x).
, Find limx→0f(x).
Solution:
We have, 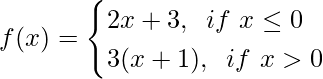
And we have to find limx→0f(x)
So for that
First we find left-hand limit:
=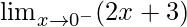
Let x = 0 – h, where h = 0.
= 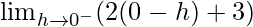
= 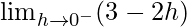
= 3
Now we find right-hand limit:
=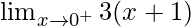
Let x = 0 + h, where h = 0.
=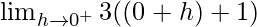
=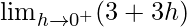
= 3
Here, Left-hand limit = Right-hand limit,
Hence, limx→0f(x) = 3
Question 8(ii). If 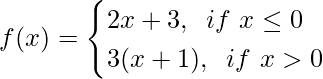 , Find limx→1f(x).
, Find limx→1f(x).
Solution:
We have, 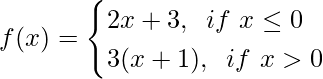
And we have to find limx→1f(x)
So for that
First we find left-hand limit:
=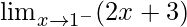
Let x = 1 – h, where h = 0.
= 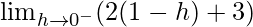
= 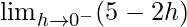
= 5
Now we find right-hand limit:
=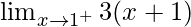
Let x = 1 + h, where h = 0.
=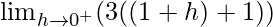
= 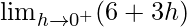
= 6
Here, Left-hand limit ≠ Right-hand limit, so limx→1f(x) does not exist.
Question 9. Find limx→1f(x) Where 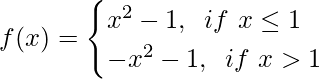
Solution:
We have, 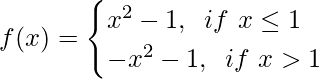
And we have to find limx→1f(x)
So for that
First we find left-hand limit:
=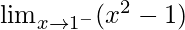
Let x = 1 – h, where h = 0.
= 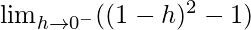
=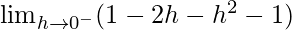
= 0
Now we find right-hand limit:
=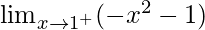
Let x = 1 + h, where h = 0.
= 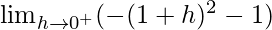
= 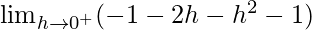
= -2
Here, Left-hand limit ≠ Right-hand limit, so, limx→1f(x) does not exist.
Question 10. Evaluate limx→0f(x), where 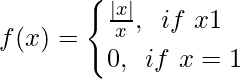
Solution:
We have, 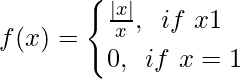
And we have to find limx→0f(x)
So for that
First we find left-hand limit:
=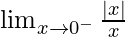
Let x = 0 – h, where h = 0.
= 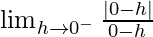
= 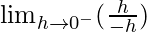
= -1
Now we find right-hand limit:
=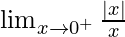
Let x = 0 + h, where h = 0.
= 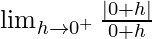
= 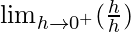
= 1
Here, Left-hand limit ≠ Right-hand limit, so, limx→0f(x) does not exist.
Question 11. Let a1, a2,……….an be fixed real number such that f(x) = (x – a1)(x – a2)……..(x-an). What is limx→a1f(x)? Compute limx→af(x).
Solution:
We have, f(x) = (x – a1)(x – a2)……..(x – an)
![Rendered by QuickLaTeX.com \lim_{x→a_1}f(x)=\lim_{x→a_1}[(x-a_1)(x-a_2)........(x-a_n)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6d3ef6b768e00820dfb686679b9475fa_l3.png)
Now, put x = a1
= (a1 – a1)(a1 – a2)……..(a1 – an)
= 0
Now, limx→af(x) = limx→a[(x – a1)(x – a2)……..(x – an)]
Now, put x = a
= (a – a1)(a – a2)……..(a – an)
Hence, limx→af(x) = (a – a1)(a – a2)……..(a – an)
Question 12. Find limx→1+[1/(x – 1)].
Solution:
We have to find limx→1+[1/(x – 1)]
=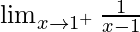
Let x = 1 + h, where h = 0.
=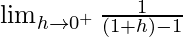
=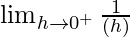
= ∞
Hence, limx→1+[1/(x – 1)] = ∞
Question 13(i). Evaluate the following one-sided limits: limx→2+[(x – 3)/(x2 – 4)]
Solution:
We have, 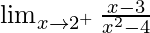
Let x = 2 + h, where h = 0.
=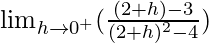
= 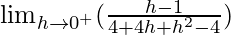
= 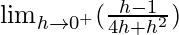
= -∞
Question 13(ii). Evaluate the following one-sided limits: limx→2–[(x – 3)/(x2 – 4)]
Solution:
We have,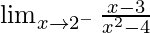
Let x = 2 – h, where h = 0.
= 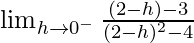
= 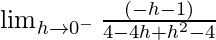
= 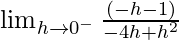
= ∞
Question 13(iii). Evaluate the following one-sided limits: limx→0+[1/3x]
Solution:
We have, limx→0+[1/3x]
Let x = 0 + h, where h = 0.
= Limh→0+[1/3(0+h)]
= Limh→0+[1/(3h)]
= ∞
Question 13(iv). Evaluate the following one-sided limits: limx→-8+[2x/(x + 8)]
Solution:
We have, limx→-8+[2x/(x + 8)]
Let x = -8 + h, where h = 0.
= limx→0+[2(-8 + h)/(-8 + h + 8)]
= Limh→0+[(2h – 16)/(h)]
= -∞
Question 13(v). Evaluate the following one-sided limits: limx→0+[2/x1/5]
Solution:
We have, limx→0+[2/x1/5]
Let x = 0 + h, where h = 0.
= Limh→0+[2/(0 + h)1/5]
= ∞
Question 13(vi). Evaluate the following one-sided limits: limx→(π/2)–[tanx]
Solution:
We have, limx→(π/2)–[tanx]
Let x = 0 – h, where h = 0.
= limh→0–[tan(π/2 – h)]
= limx→0–[cot h]
= ∞
Question 13(vii). Evaluate the following one-sided limits: limx→(-π/2)+[secx]
Solution:
We have, limx→(-π/2)+[secx]
Let x = 0 + h, where h = 0.
= limh→0+[secx(-π/2 + h)]
= limh→0+[cosec h]
= ∞
Question 13(viii). Evaluate the following one-sided limits: limx→0–[(x2 – 3x + 2)/x3 – 2x2]
Solution:
We have, limx→0-[x2 – 3x + 2/x3 – 2x2]
= Limx→0-[(x – 1)(x – 2)/x2(x – 2)]
= Limx→0-[(x – 1)/x2]
Let x = 0 – h, where h = 0.
= Limh→0-[(0 – h – 1)/(0 – h)2]
= -∞
Question 13(ix). Evaluate the following one-sided limits: limx→-2+[(x2 – 1)/(2x + 4)]
Solution:
We have, limx→-2+[(x2 – 1)/(2x + 4)]
Let x = -2 + h, where h = 0.
= Limh→-0+[(-2 + h)2 – 1)/2(-2 + h) + 4]
= Limh→-0+[(-2 + h)2 – 1)/(-4 + 4 + h)]
= (4 – 1)/0
= ∞
Question 13(x). Evaluate the following one-sided limits: limx→0-[2 – cotx]
Solution:
We have, limx→0-[2 – cotx]
Let x = 0 – h, where h = 0.
= Limh→0-[2 – cot(0 – h)]
= Limh→0-[2 + cot(h)]
= 2 + ∞
= ∞
Question 13(xi). Evaluate the following one-sided limits. limx→0-[1 + cosecx]
Solution:
We have, limx→0-[1 + cosecx]
Let x = 0 – h, where h = 0.
= Limh→0-[1 + cosec(0 – h)]
= Limh→0-[1 – cosec(h)]
= 1 – ∞
= -∞
Question 14. Show that Limx→0e-1/x does not exist.
Solution:
Let, f(x) = Limx→0e-1/x
So for that
First we find left-hand limit:
= 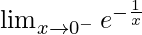
Let x = 0 – h, where h = 0.
= 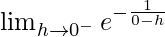
=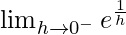
= e∞
= ∞
Now we find right-hand limit:
=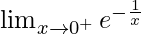
Let x = 0 + h, where h = 0.
= 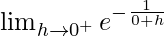
=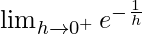
= e-∞
= 0
Here, Left-hand limit ≠ Right-hand limit, so, Limx→0e-1/x does not exist.
Question 15(i). Find Limx→2[x]
Solution:
We have, Limx→2[x], where [] is Greatest Integer Function
So for that
First we find left-hand limit:
=![Rendered by QuickLaTeX.com \lim_{x\to0^-}[x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-abfed9a6ac029028a138d80f48e1b614_l3.png)
Let x = 2 – h, where h = 0.
= ![Rendered by QuickLaTeX.com \lim_{h\to0^-}[2 - h]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-08f1fa6f9d26734d281914a97c2263a6_l3.png)
= 1
Now we find right-hand limit:
= ![Rendered by QuickLaTeX.com \lim_{x\to0^+}[x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fa4eed5c1acddeb90732a524dafa1d1c_l3.png)
Let x = 2 + h, where h = 0.
= ![Rendered by QuickLaTeX.com \lim_{h\to0^+}[2+h]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ea79f6a387f4f618b0b0ea187a84f356_l3.png)
= 2
Here, Left-hand limit ≠ Right-hand limit, so, Limx→2[x] does not exist.
Question 15(ii). Find Limx→5/2[x]
Solution:
We have, Limx→2[x], where [] is Greatest Integer Function
So for that
First we find left-hand limit:
=![Rendered by QuickLaTeX.com \lim_{x\to\frac{5}{2}^-}[x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-20a9be9826b310ade647ed2260bfecd0_l3.png)
Let x = 5/2 – h, where h = 0.
= ![Rendered by QuickLaTeX.com \lim_{h\to0^-}[\frac{5}{2} - h]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc1541f70b89ed6977e11c04b0cea47a_l3.png)
= 2
Now we find right-hand limit:
=![Rendered by QuickLaTeX.com \lim_{x\to\frac{5}{2}^+}[x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8e252e7d91096689e0ed8718d905662d_l3.png)
Let x = 5/2 + h, where h = 0.
= ![Rendered by QuickLaTeX.com \lim_{h\to0^+}[\frac{5}{2}+h]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dfa3c4ba7c01bcc333842f00b60d4566_l3.png)
= 2
Here, Left-hand limit = Right-hand limit, so, Limx→5/2[x] = 2
Question 15(iii). Find Limx→1[x]
Solution:
We have, Limx→1[x], where [] is Greatest Integer Function
So for that
First we find left-hand limit:
=![Rendered by QuickLaTeX.com \lim_{x\to1^-}[x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d4443ba3eb8787b45175d6db4dd618eb_l3.png)
Let x = 1 – h, where h = 0.
= ![Rendered by QuickLaTeX.com \lim_{h\to0^-}[1-h]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bcd744e9f7f1c1cc7a76892f74264bb0_l3.png)
= 0
Now we find right-hand limit:
= ![Rendered by QuickLaTeX.com \lim_{x\to1^+}[x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8b1a1a6ffbc95f603ef4dd08726ff544_l3.png)
Let x = 1 + h, where h = 0.
= ![Rendered by QuickLaTeX.com \lim_{h\to0^+}[1+h]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d5f48e70b7648e86f24d06b80ea3d4b3_l3.png)
= 1
Here, Left-hand limit = Right-hand limit, so, Limx→1[x] does not exist.
Question 16. Prove that Limx→a+[x] = [a]. Also prove that Limx→1-[x] = 0.
Solution:
We have, ![Rendered by QuickLaTeX.com \lim_{x\to a^+}[x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a9e3a002811ce69d39610a35c57fb3c7_l3.png)
Let x = a + h, where h = 0.
= Limh→0-[(a + h)]
= a
Also, ![Rendered by QuickLaTeX.com \lim_{x\to1^-}[x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d4443ba3eb8787b45175d6db4dd618eb_l3.png)
Let x = 1 – h, where h = 0.
= Limh→0[(1 – h)]
= 0
Question 17. Show that Limx→2+(x/[x]) ≠ Limx→2-(x/[x]).
Solution:
We have to show Limx→2+(x/[x]) ≠ Limx→2-(x/[x])
So, R.H.L
We have, ![Rendered by QuickLaTeX.com \lim_{x\to2^-}\frac{x}{[x]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3cd2175d828df9f9b51cd2430e0d8e98_l3.png) , where [] is greatest Integer Function
, where [] is greatest Integer Function
Let x = 2 – h, where h = 0.
= Limh→0-[(2 – h)/|[2 – h]]
= 2/1
= 2
Now, L.H.L
We have, ![Rendered by QuickLaTeX.com \lim_{x\to2^+}\frac{x}{[x]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-62101408521094c32f3995bcf8f0c434_l3.png) , where [] is greatest Integer Function
, where [] is greatest Integer Function
Let x = 2 + h, where h = 0.
= Limh→0+[(2 + h)/|[2 + h]]
= 2/2
= 1
Hence, Left-hand limit≠Right-hand limit
Question 18. Find Limx→3+(x/[x]). Is it equal to Limx→3-(x/[x])
Solution:
We have, ![Rendered by QuickLaTeX.com \lim_{x\to3^-}\frac{x}{[x]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-59185bddf1e76d16d8ea4dd073b3faf3_l3.png) Where [] is Greatest Integer Function
Where [] is Greatest Integer Function
Let x = 3 – h, where h = 0.
= Limh→0-[(3 – h)/|[3 – h]]
= 3/2
Also, ![Rendered by QuickLaTeX.com \lim_{x\to3^+}\frac{x}{[x]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-10487e1345ebf4352edbcf5c75014088_l3.png)
Let x = 3 + h, where h = 0.
= Limh→0+[(3 + h)/|[3 + h]]
= 3/3
= 1
Hence, Left-hand limit≠Right-hand limit
Question 19. Find Limx→5/2[x]
Solution:
We have to find Limx→5/2[x], where [] is Greatest Integer Function
So for that
First we find left-hand limit:
= ![Rendered by QuickLaTeX.com \lim_{x\to\frac{5}{2}^-}[x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-20a9be9826b310ade647ed2260bfecd0_l3.png)
Let x = 5/2 – h, where h = 0.
= Limh→0-[(5/2 – h)]
= 2
Now we find right-hand limit:
![Rendered by QuickLaTeX.com =\lim_{x\to\frac{5}{2}^+}[x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5711c85e3ede5c6a964b9b977963c973_l3.png)
Let x = 5/2 + h, where h = 0.
= Limh→0+[(5/2+h)]
= 2
Hence, Left-hand limit = Right-hand limit, so Limx→5/2[x] = 2
Question 20. Evaluate Limx→2f(x), where ![Rendered by QuickLaTeX.com f(x)= \begin{cases} x-[x], \hspace{0.2cm}x<2\\ 4 , \hspace{0.2cm}x=2\\ x+k,\hspace{0.2cm}x>2 \end{cases}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-577fed33519f916b95add7cf0f5f5071_l3.png)
Solution:
We have, ![Rendered by QuickLaTeX.com f(x)= \begin{cases} x-[x], \hspace{0.2cm}x<2\\ 4 , \hspace{0.2cm}x=2\\ x+k,\hspace{0.2cm}x>2 \end{cases}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-577fed33519f916b95add7cf0f5f5071_l3.png)
We have to find Limx→2f(x)
So for that
First we find left-hand limit:
= ![Rendered by QuickLaTeX.com \lim_{x\to0^-}(x-[x])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ba2add287c3dfebc7f2f9f3541752023_l3.png)
Let x = 2 – h, where h = 0.
= Limh→0-{(2 – h) – [2 – h]}
= 2 – 1
= 1
Now we find right-hand limit:
=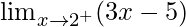
Let x = 2 + h, where h = 0.
= Limh→0-[3(2 + h) – 5]
= 6 – 5
= 1
Hence, Left-hand limit = Right-hand limit, so, Limx→2f(x) = 1
Question 21. Show that Limx→0sin(1/x) does not exist.
Solution:
Let, f(x) = Limx→0sin(1/x)
First we find left-hand limit:
= 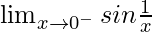
Let x = 0 – h, where h = 0.
= Limh→0sin[1/(0 – h)]
= -Limh→0sin[1/(h)]
An oscillating number lies between -1 to +1.
So left hand limit does not exists.
Similarly, right-hand limit is also oscillating.
So, Limx→0sin(1/x) does not exist.
Question 22. Let 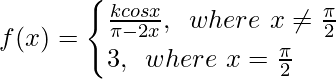 and if lim x→π/2 f(x) = f(π/2), find the value of k.
and if lim x→π/2 f(x) = f(π/2), find the value of k.
Solution:
We have 
First we find left-hand limit:
= 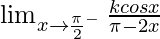
Let x = π/2 – h, where h = 0.
=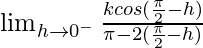
= k cos(π/2 – π/2)/π
= k/π
Now we find right-hand limit:
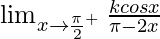
Let x = π/2 + h, where h = 0.
=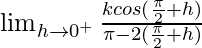
= k cos(π/2 + π/2)/-π
= k/π
Hence, Left-hand limit = Right-hand limit, so
lim x→π/2 f(x) = f(π/2)
k/π = 3
k = 3π
Share your thoughts in the comments
Please Login to comment...