Class 12 RD Sharma Solutions – Chapter 7 Adjoint and Inverse of a Matrix – Exercise 7.2
Last Updated :
28 Mar, 2021
Find the inverse of each of the following matrices by using elementary row transformation(Questions 1- 16):
Question 1. 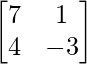
Solution:
Here, A = 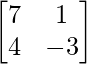
A = AI
Using elementary row operation
⇒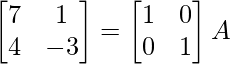
R1 -> 1/7R1
⇒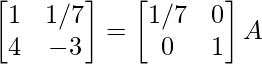
R2 -> R2 – 4R1
⇒
R2 -> (-7/25)R2
⇒
R1 -> R1 – 1/7R2
⇒
Therefore, A-1 =
Question 2. 
Solution:
Here, A = 
A = AI
Using elementary row operation
⇒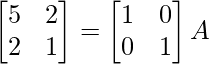
R1 -> 1/5R1
⇒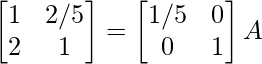
R1 -> R2 – 2R1
⇒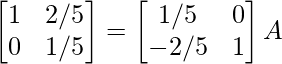
R2 -> 5R2
⇒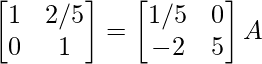
R1 -> R1 – 2/5R2
⇒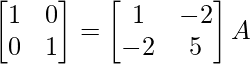
Therefore, A-1= 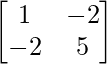
Question 3. 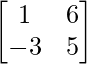
Solution:
Here, A = 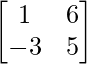
A = AI
Using elementary row operation
⇒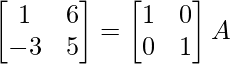
R2 -> R2 + 3R1
⇒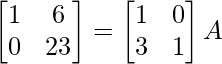
R2 -> 1/23R2
⇒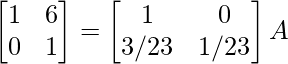
R1 -> R1 – 6R1
⇒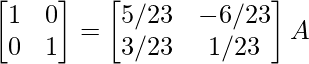
Therefore, A-1 = 
Question 4. 
Solution:
Here, 
A = AI
Using elementary row operation
⇒
R1 -> 1/2R1
⇒
R2 -> R2 – R1
⇒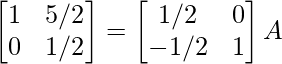
R2 -> 2R2
⇒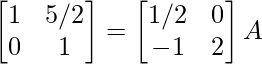
R1 -> R1 – 5/2R2
⇒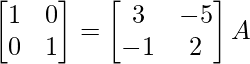
Therefore, A-1 = 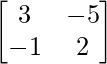
Question 5. 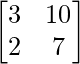
Solution:
Here, A = 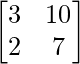
A = AI
⇒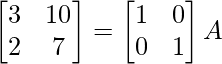
R1 -> 1/3R1
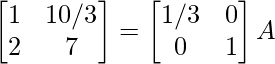
R2 -> R2 – 2R1
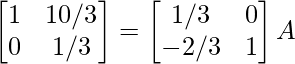
R2 -> 3R2
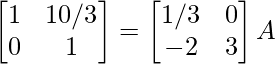
R1 -> R1 – 10/3R2
⇒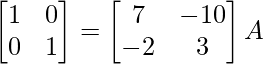
Therefore, A-1 = 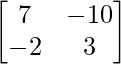
Question 6. 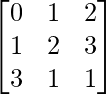
Solution:
Here, A = 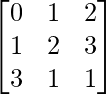
A = IA
⇒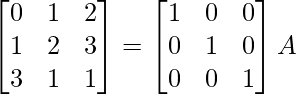
R1 ↔ R2
⇒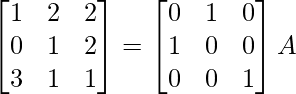
R3 -> R3 – 3R1
⇒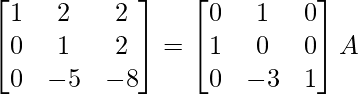
R1 -> R1 – 2R2, R3 -> R3 + 5R2
⇒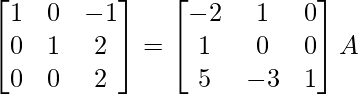
R3 -> R3/2
⇒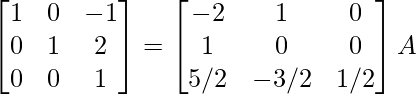
R1 -> R1 + R3, R2 -> R2 – 2R3
⇒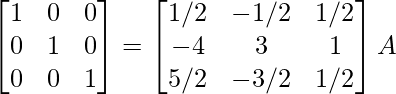
Therefore, A-1 =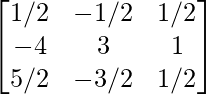
Question 7. 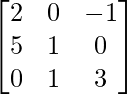
Solution:
Here, A = 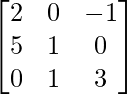
A = IA
⇒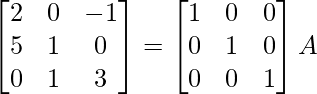
R1 -> R1/2
⇒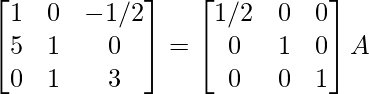
R2 -> R2 – 5R1
⇒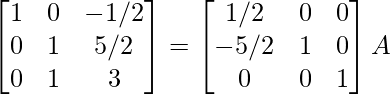
R3 -> R3 – R2
⇒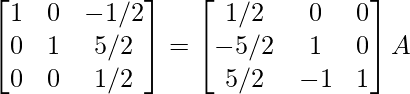
R3 -> 2R3
⇒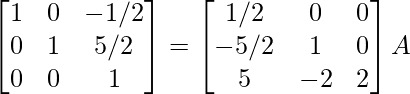
R1 -> R1 + 1/2R3, R2 -> R2 – 5/2R3
⇒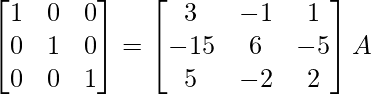
Therefore, A-1 = 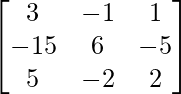
Question 8. 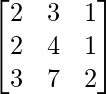
Solution:
Here, A = 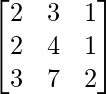
A = IA
⇒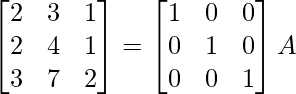
R1 -> 1/2R1
⇒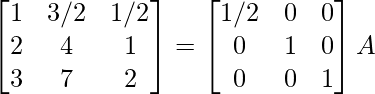
R2 -> R2 – 2R1, R3 -> R3 – 3R1
⇒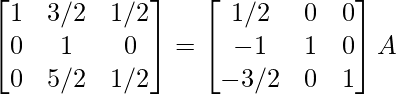
R1 -> R1 – 3/2R2, R3 -> R3 – 5/2R2
⇒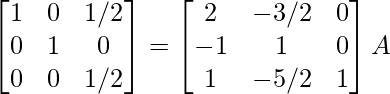
R3 -> 2R3
⇒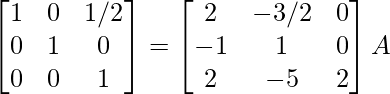
R1 -> R1 – 1/2R3
⇒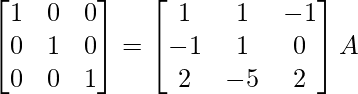
Therefore, A-1 = 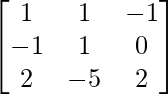
Question 9. 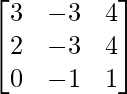
Solution:
Here, A = 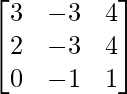
A = IA
⇒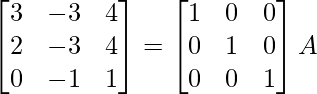
R1 -> 1/3R1
⇒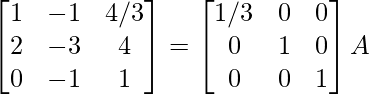
R2 -> R2 – 2R1
⇒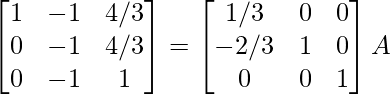
R2 -> (-1)R2
⇒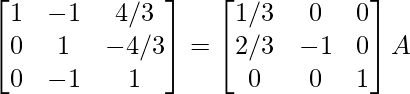
R1 -> R1 + R2, R3 -> R3 + R2
⇒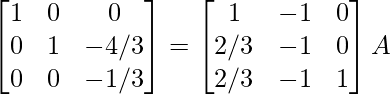
R3 -> (-3)R3
⇒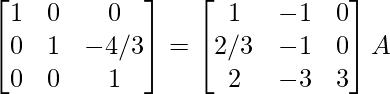
R2 -> R2 + 4/3R3
⇒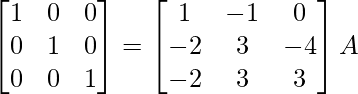
Therefore, A-1 = 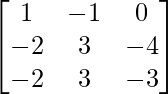
Question 10. 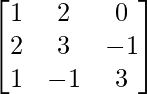
Solution:
Here, A = 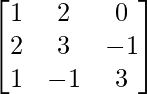
⇒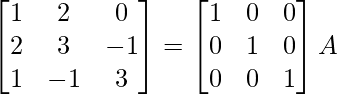
R2 -> R2 – 2R1, R3 -> R3 – R1
⇒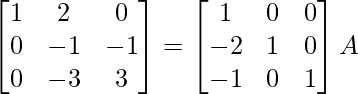
R2 -> (-1)R2
⇒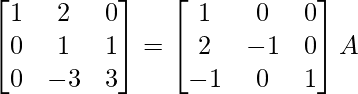
R1 -> R1 – 2R2, R3 -> R3 + 3R2
⇒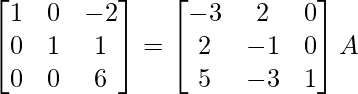
R3 -> R3/6
⇒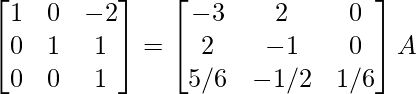
R1 -> R1 + 2R3, R2 -> R2 – R3
⇒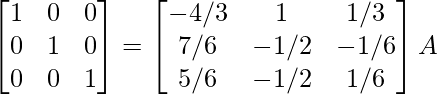
Therefore, A-1 = 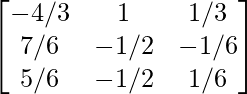
Question 11. 
Solution:
Here, A = 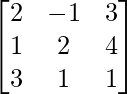
A = IA
⇒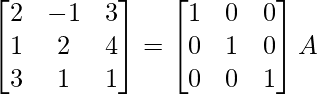
R1 -> R1/2
⇒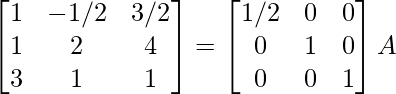
R2 -> R2 – R1, R3 -> R3 – 3R1
⇒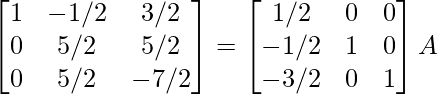
R2 -> (2/5)R2
⇒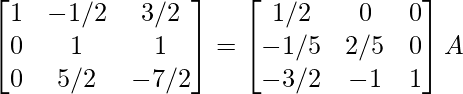
R1 -> R1 + 1/2 R2, R3 -> R3 – 5/2R2
⇒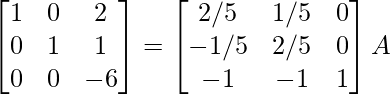
R3 -> R3/-6
⇒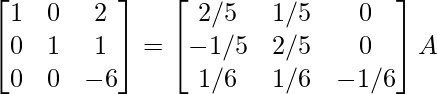
R2 -> R2 – R3, R1 -> R1 – 2R3
⇒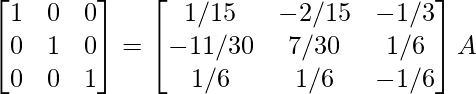
Therefore, A-1 = 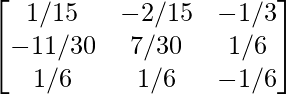
Question 12. 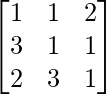
Solution:
Here, A = 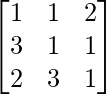
A = IA
⇒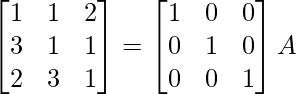
R2 -> R2 – 3R1, R3 -> R3 – 2R1
⇒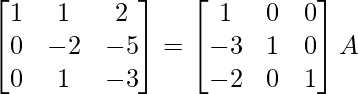
R2 -> R2/(-2)
⇒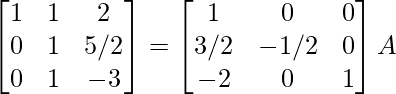
R1 -> R1 – R2, R3 -> R3 – R2
⇒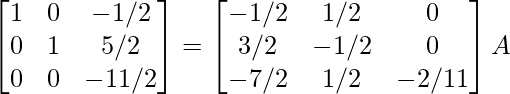
R3 -> (-2/11)R3
⇒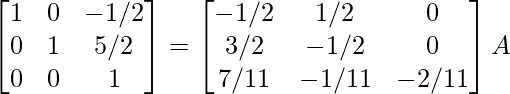
R1 -> R1 + 1/2R3, R2 -> R2 – 5/2R3
⇒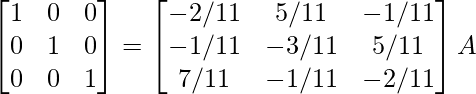
Therefore, A-1 = 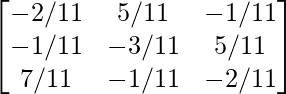
Question 13. 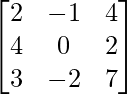
Solution:
Here, A = 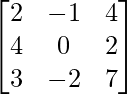
A = IA
⇒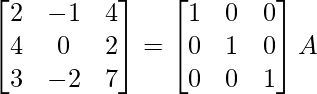
R1 -> 1/2R1
⇒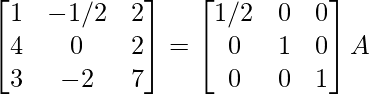
R2 -> R2 – 4R1, R3 -> R3 – 3R1
⇒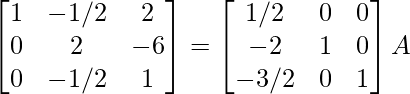
R2 -> 1/2R2
⇒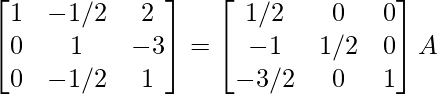
R1 -> R1 + 1/2R2, R3 -> R3 + 1/2R2
⇒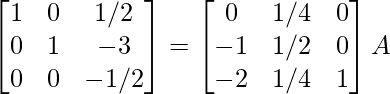
R3 -> (-2)R3
⇒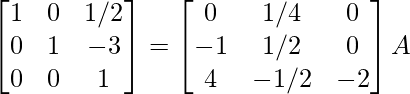
R1 -> R1 – 1/2R3, R2 -> R2 + 3R3
⇒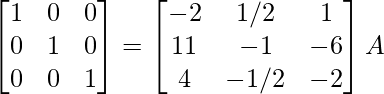
Therefore, A-1 = 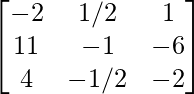
Question 14. 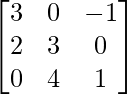
Solution:
Here, A = 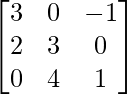
A = IA
⇒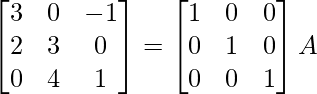
R1 -> (1/3)R1
⇒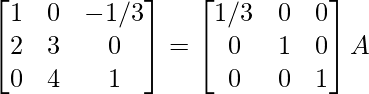
R2 -> R2 – 2R1
⇒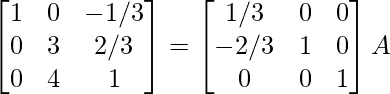
R2 -> (1/3)R2
⇒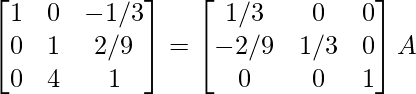
R3 -> R3 – 4R2
⇒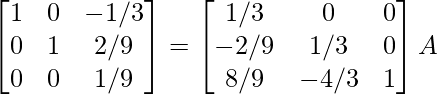
R3 -> 9R3
⇒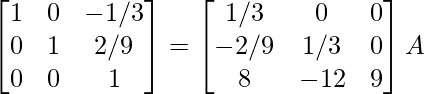
R1 -> R1 + 1/3R3, R2 -> R2 – 2/9R3
⇒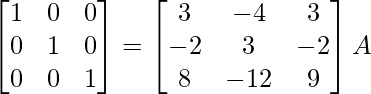
Therefore, A-1 = 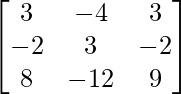
Question 15. 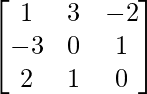
Solution:
Here, A = 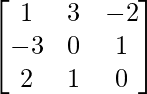
A = IA
⇒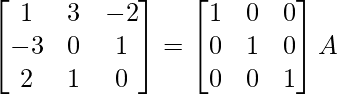
R2 -> 3R1 + R2, R3 -> R3 – 2R1
⇒
R1 -> R1 – 3R2, R3 -> R3 + 5R2
⇒
R2 -> R2 + 5/9R3, R1 -> R1 + 1/3R3
⇒
Therefore, A-1 = 
Question 16. 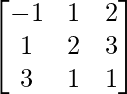
Solution:
Here, A= 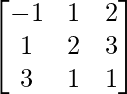
A = IA
⇒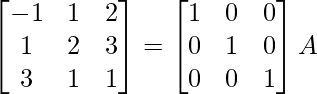
R1 -> (-1)R1
⇒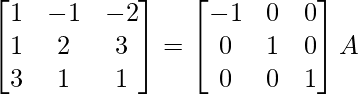
R2 -> R2 – R1, R3 -> R3 – 3R1
⇒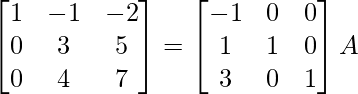
R2 -> R2/3
⇒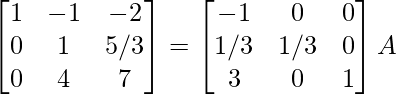
R1 -> R1 + R2, R3 -> R3 – 4R2
⇒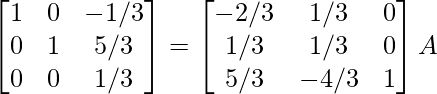
R3 -> R3/3
⇒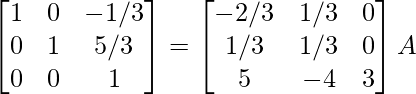
R1 -> R1 + 1/3R3, R2 -> R2 – 5/3R3
⇒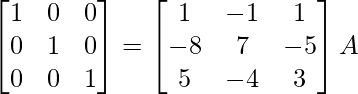
Therefore, A-1 = 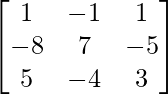
Share your thoughts in the comments
Please Login to comment...