Class 12 NCERT Solutions- Mathematics Part I – Chapter 2 Inverse Trigonometric Functions – Miscellaneous Exercise on Chapter 2
Last Updated :
03 Apr, 2024
Question 1. Find the value of 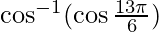
Solution:
We know that 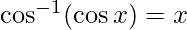
Here, ![Rendered by QuickLaTeX.com \frac {13\pi} {6} \notin [0,\pi].](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8bf1146ccd83f2f3fc6b1a53855a4f4f_l3.png)
Now, 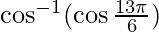 can be written as :
can be written as :
![Rendered by QuickLaTeX.com {\cos }^{-1}(\cos \frac {13\pi} {6})={\cos }^{-1}[\cos( 2\pi+\frac {\pi} {6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7068385249f0a55997c870457e5be945_l3.png) , where
, where ![Rendered by QuickLaTeX.com \frac{\pi} {6} \in [0,\pi].](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9445b99add3c8a8d5ea193997a32f317_l3.png)
Hence, the value of 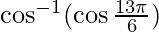 = π/6
= π/6
Question 2. Find the value of 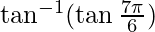
Solution:
We know that 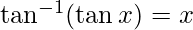
Here, 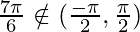
Now, 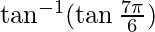 can be written as:
can be written as:
![Rendered by QuickLaTeX.com \tan^{-1}(\tan \frac {7\pi}{6})=\tan^{-1}[\tan( 2\pi -\frac {5\pi}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a1a8b64ae4f7ab91a80c493d58e3b3a3_l3.png)
![Rendered by QuickLaTeX.com -[\tan(2\pi-x)=-\tan x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-de5af46d77e45866034da7997808bdc3_l3.png)
![Rendered by QuickLaTeX.com \tan^{-1}[-\tan(\frac {5\pi}{6}) ]=\tan^{-1}[\tan(-\frac {5\pi}{6})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eaab23825145e5e827674d17546df35d_l3.png)
![Rendered by QuickLaTeX.com =\tan^{-1}[\tan(\pi-\frac {5\pi}{6})]=\tan^{-1}[\tan( \frac {\pi}{6})],](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e5e1a0ca675faf6685768ee72d9f403d_l3.png) where
where 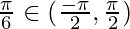
Hence, the value of 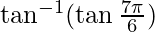 = π/6
= π/6
Question 3. Prove 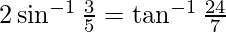
Solution:
Let 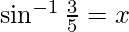 -(1)
-(1)
sin x = 3/5
So,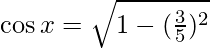 = 4/5
= 4/5
tan x = 3/4
Hence, 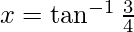
Now put the value of x from eq(1), we get
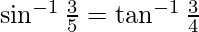
Now, we have
L.H.S 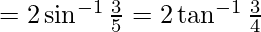
= 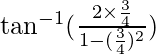 –
–![Rendered by QuickLaTeX.com [2\tan^{-1} x=\tan^{-1} \frac{2x}{1-x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-16d00e19ec11077dfaac4aed84d534dc_l3.png)
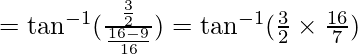
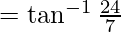
Hence, proved.
Question 4. Prove 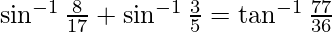
Solution:
Let 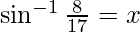
Then sin x = 8/17
cos x =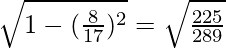 = 15/17
= 15/17
Therefore, 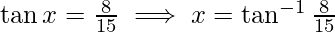
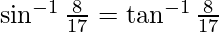 -(1)
-(1)
Now, let 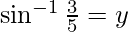
Then, sin y = 3/5
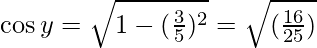 = 4/5
= 4/5
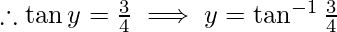
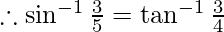 -(2)
-(2)
Now, we have:
L.H.S.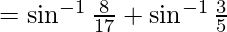
From equation(1) and (2), we get
= 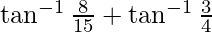
= 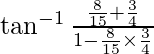
= 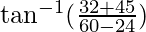 –
–![Rendered by QuickLaTeX.com [\tan^{-1} x + \tan^{-1} y=\tan^{-1} \frac{x+y}{1-xy}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8d87c3b7e447db71063e1a3cb9af70db_l3.png)
= 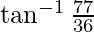
Hence proved
Question 5. Prove 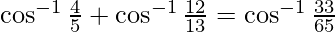
Solution:
Let 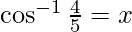
Then, cos x = 4/5
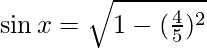 = 3/5
= 3/5
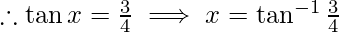
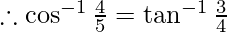 -(1)
-(1)
Now let 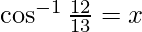
Then, cos y = 3/4
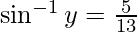
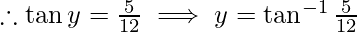
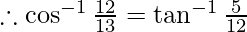 -(2)
-(2)
Let 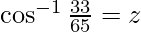
Then, cos z = 33/65
sin z = 56/65
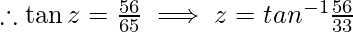
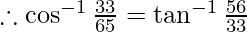 -(3)
-(3)
Now, we will prove that :
L.H.S. 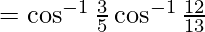
From equation (1) and equation (2)
= 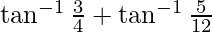
= 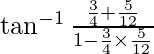 –
–![Rendered by QuickLaTeX.com [\tan^{-1} x +\tan^{-1} y=\tan^{-1} \frac{x+y}{1-xy}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-043bd03a2b99baf2285a8debc77321e7_l3.png)
= 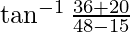
= 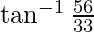
Using equation(3)
= 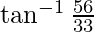
Hence proved
Question 6. Prove 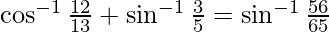
Solution:
Let 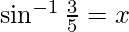
Then, sin x = 3/5
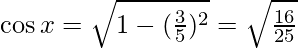 = 4/5
= 4/5
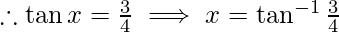
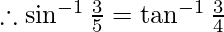 -(1)
-(1)
Now, let 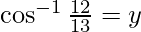
Then, cos y = 12/13 and sin y = 5/13
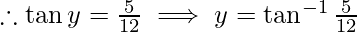
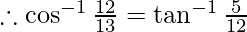 -(2)
-(2)
Let 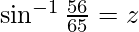
Then, sin z = 56/65 and cos z = 33/65
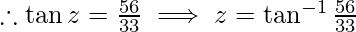
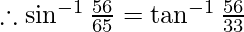 -(3)
-(3)
Now, we have:
L.H.S.=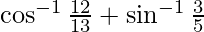
From equation(1) and equation(2)
=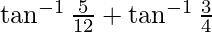
= 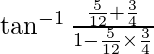 –
–![Rendered by QuickLaTeX.com [\tan^{-1} x +\tan^{-1} y=\tan^{-1} \frac{x+y}{1-xy}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-382f3984afb310d0be26f7a9ef48a6bc_l3.png)
= 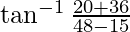
= 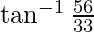
From equation (3)
= 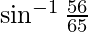
Hence proved
Question 7. Prove 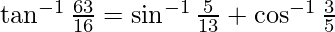
Solution:
Let 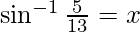
Then, sin x = 5/13 and cos x = 12/13.
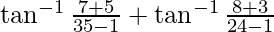
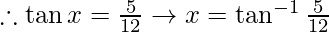
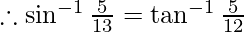 -(1)
-(1)
Let 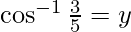
Then, cos y = 3/5 and sin y = 4/5
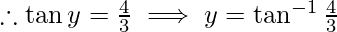
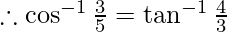 -(2)
-(2)
From equation(1) and (2), we have
R.H.S.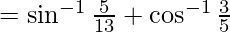
=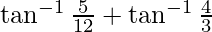
= 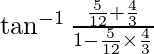 –
–![Rendered by QuickLaTeX.com [\tan^{-1} x +\tan^{-1} y=\tan^{-1} \frac{x+y}{1-xy}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-043bd03a2b99baf2285a8debc77321e7_l3.png)
=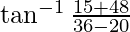
=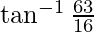
L.H.S = R.H.S
Hence proved
Question 9. Prove ![Rendered by QuickLaTeX.com \tan^{-1} \sqrt x= \frac{1}{2} \cos^{-1} (\frac{1-x}{1+x}),x\in[0,1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a7d48cc4f03c433056decf63874d6881_l3.png)
Solution:
Let x = tan2θ
Then,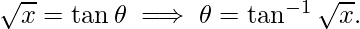
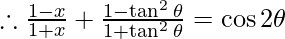
Now, we have
R.H.S = 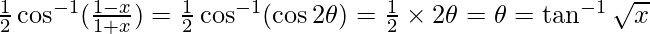
L.H.S = R.H.S
Hence proved
Question 9. Prove 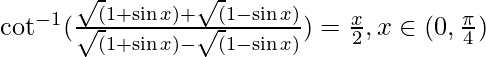
Solution:
Consider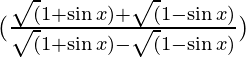
By rationalizing
=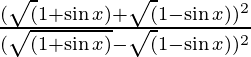
=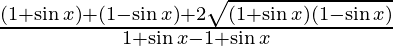
=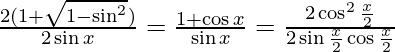
= 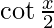
L.H.S = 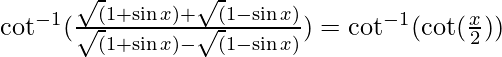 = x/2
= x/2
L.H.S = R.H.S
Hence proved
Question 10. Prove 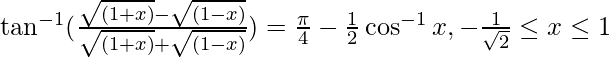
Solution:
Put 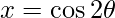 so that,
so that, 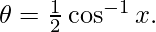
Then, we have :
LHS = 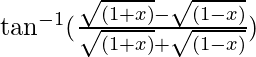
= 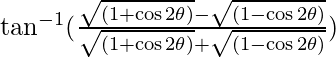
= 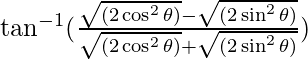
= 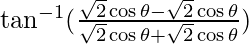
= 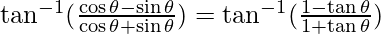
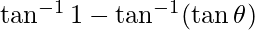 –
– ![Rendered by QuickLaTeX.com [\tan^{-1}(\frac{x-y}{1+xy})]=\tan^{-1}x+\tan^{-1}y](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c7425ab59a752f744d5fc4b1a09c1c61_l3.png)
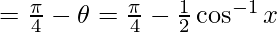
L.H.S = R.H.S
Hence Proved
Question 11. Solve 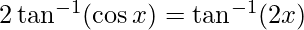
Solution:
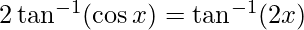
=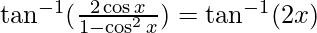 –
–![Rendered by QuickLaTeX.com [2 \tan^{-1} x=\tan^{-1} \frac{2x}{1-x^{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-26977a780ea52f253ede5d3ab7b9aaa6_l3.png)
= 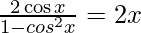
= 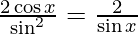
= cos x/sin x
= cot x =1
Therefore, x = π/4
Question 12. Solve 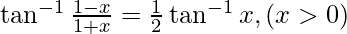
Solution:
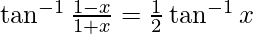
Let x = tanθ
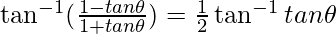
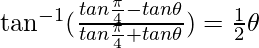
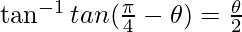
π/4 – θ = θ/2
θ = π/6
So, x = tan(π/6) = 1/√3
Question 13. Solve 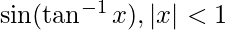 is equal to
is equal to
(A) 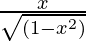 (B)
(B) 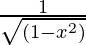 (C)
(C) 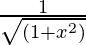 (D)
(D) 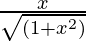
Solution:
Let tan y = x, 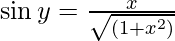
Let 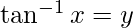 Then,
Then,
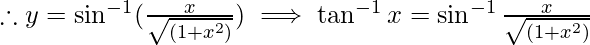
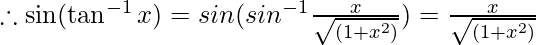
So, the correct answer is D.
Question 14. Solve 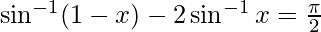 , then x is equal to
, then x is equal to
(A) 0, 1/2 (B) 1, 1/2 (C) 0 (D) 1/2
Solution:
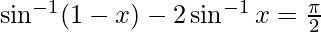
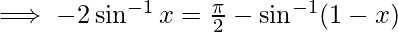
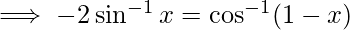 -(1)
-(1)
Let 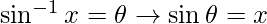
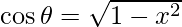
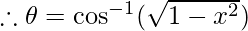
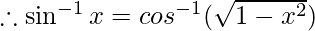
Therefore, from equation(1), we have
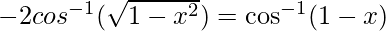
Put x = siny then, we have:
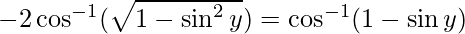
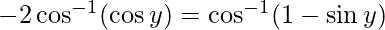
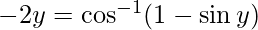
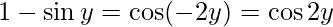
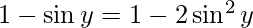
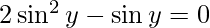
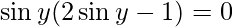
sin y = 0 or 1/2
x = 0 or x = 1/2
But, when x = 1/2 it can be observed that:
L.H.S. = 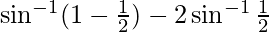
= 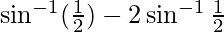
= 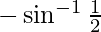
= 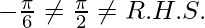
x = 1/2 is not the solution of given equation.
Thus, x = 0
Hence, the correct answer is C
Prove 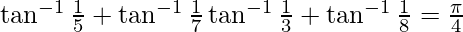
Solution:
L.H.S.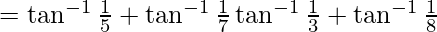
= 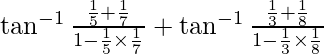 –
–![Rendered by QuickLaTeX.com [\tan^{-1} x +\tan^{-1} y=\tan^{-1} \frac{x+y}{1-xy}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-043bd03a2b99baf2285a8debc77321e7_l3.png)
= 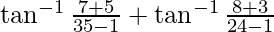
= 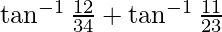
= 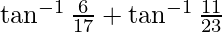
= 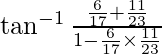
= 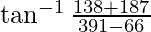
= 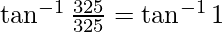
= π/4
L.H.S = R.H.S
Hence proved
Prove 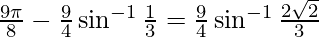
Solution:
L.H.S. = 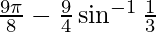
= 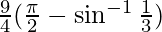
Using 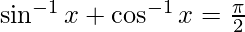
= 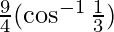 -(1)
-(1)
Now, let 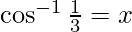 Then,
Then, 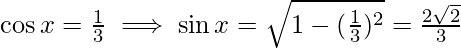
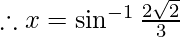
Using equation(1), we get,
= 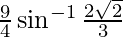
L.H.S = R.H.S
Hence Proved
Solve 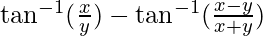 is equal to
is equal to
(A) π/2 (B) π/3 (C) π/4 (D) -3π/4
Solution
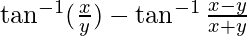
![Rendered by QuickLaTeX.com \tan^{-1}[\frac{\frac{x}{y}-\frac{x-y}{x+y}}{1+\frac{x}{y} \times\frac{x-y}{x+y}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4a7532615b79c6e89822861f2e1f933e_l3.png) –
–![Rendered by QuickLaTeX.com [\tan^{-1}x+\tan^{-1}y=[\tan^{-1}(\frac{x-y}{1+xy})]]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e2f382c49c2c952d1bf7851e302118aa_l3.png)
![Rendered by QuickLaTeX.com \tan^{-1}[\frac {\frac {x(x+y)-y(x-y)} {y(x+y)} } {\frac {y(x+y)+x(x-y)} {y(x+y)}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3a051f04145b11254e8e7e2e47048e18_l3.png)
![Rendered by QuickLaTeX.com {\tan}^{-1}[{\frac {x^2+xy-xy+y^2} {xy+y^2+x^2-xy}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-87208a1a84d0baf93ea681955a1db844_l3.png)
![Rendered by QuickLaTeX.com {\tan}^{-1}[\frac {x^2+y^2} {x^2+y^2}]=tan^{-1}1=\frac {\pi} {4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0f2e34c2e9a766dcfaf1c177d903e61a_l3.png)
Hence, the correct answer is C
Share your thoughts in the comments
Please Login to comment...