Class 12 RD Sharma Solutions – Chapter 29 The Plane – Exercise 29.11 | Set 1
Last Updated :
21 Jul, 2021
Question 1. Find the angle between the line 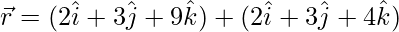 and the plane
and the plane 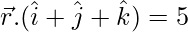 .
.
Solution:
Given that, the line is 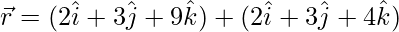 and the plane is
and the plane is 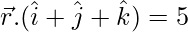 .
.
So,
As we know that the angle between a line and a plane is
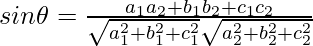
So,
⇒ 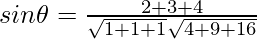
⇒ 9/√87
Question 2. Find the angle between the line 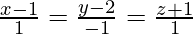 and the plane 2x + y – z = 4.
and the plane 2x + y – z = 4.
Solution:
The given line 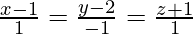 is parallel to the vector
is parallel to the vector 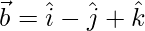 and the plane 2x + y – z = 4 is normal to the vector
and the plane 2x + y – z = 4 is normal to the vector 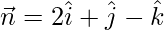 .
.
So, the angle between line and plane is
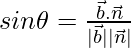
= 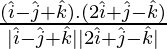
= 0
Question 3. Find the angle between the line joining the points (3, -4, -2) and (12, 2, 0) and the plane 3x – y + z = 1.
Solution:
According to the question, the line passes through A(3,- 4,- 2) and B(12, 2, 0).
So, 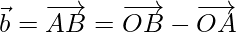
= 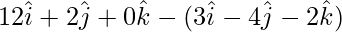
= 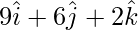
So, the line is parallel to the vector 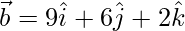 and the plane is normal to the vector
and the plane is normal to the vector 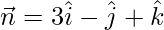
So, the angle between the line and the plane is,
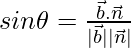
= 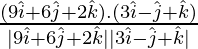
= 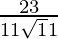
Thus, 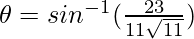 .
.
Question 4. The line 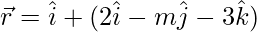 is parallel to the plane
is parallel to the plane 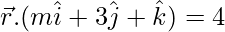 . Find m.
. Find m.
Solution:
Give that the equation of line is 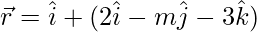 and the equation of plane is
and the equation of plane is 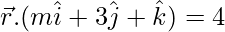
So, 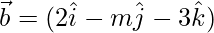
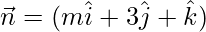
If a line is parallel to a plane, then the normal to the plane is perpendicular to the line.
⇒ 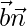
⇒ 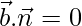
⇒ 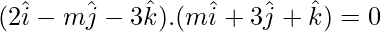
⇒ 2m – 3m – 3 = 0
⇒ – m – 3 = 0
⇒ m = –3
Question 5. Show that the line whose vector equation is 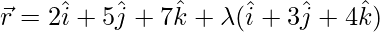 is parallel to the plane whose vector
is parallel to the plane whose vector 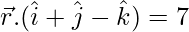 . Also, find the distance between them.
. Also, find the distance between them.
Solution:
Given that the plane passes through the point with the position vector 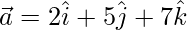 and is parallel to the vector
and is parallel to the vector 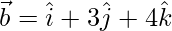 .
.
So, the normal vector 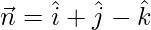 and d = 7 .
and d = 7 .
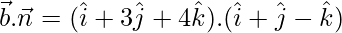
= 1 + 3 – 4
= 4 – 4
= 0
As we know that 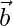 is perpendicular to
is perpendicular to 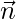
So, the distance between the line and plane is
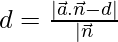
= 7/√3units.
Question 6. Find the vector equation of the line through the origin which is perpendicular to the plane 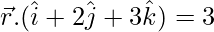 .
.
Solution:
Given that the line is perpendicular to the plane 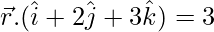
So, the line is parallel to the normal 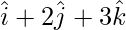 .
.
As we know that the equation of a line is pass through  and parallel to
and parallel to 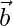 is
is 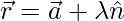
⇒ 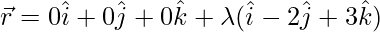
⇒ 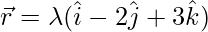
Question 7. Find the equation of the plane through (2, 3, −4) and (1, −1, 3) and parallel to the x-axis.
Solution:
Given that the equation of the plane through point (2, 3, -4) is
a(x − 2) + b(y − 3)+c(z + 4) = 0 …(1)
Since this plane passes through point (1, -1, 3).
⇒ a(1 − 2) + b( −1 − 3) + c( 3 + 4) = 0
⇒ − a − 4b + 7c = 0 …(2)
Equation(1) is parallel to x-axis and is perpendicular to the yz-plane whose equation is x = 0 or 1 . x + 0 . y + 0 . z = 0
⇒ a(1) + b(0) + c(0) = 0 …(3)
One solving eq(1), (2), and (3), we get
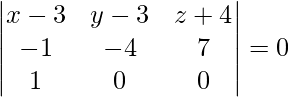
⇒ 7y + 4z – 5 = 0 is the required equation.
Question 8. Find the equation of a plane passing through the points (0, 0, 0) and (3, −1, 2) and parallel to the line 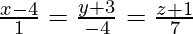
Solution:
Given that the plane pass through point(0, 0, 0), so the equation of the plane is a(x − 0) + b(y − 0)+c(z + 0) = 0.
⇒ ax + by + cz = 0 …(1)
and the same plane passes through point (3, -1, 2). So, the equation of the plane is
3a – b + 2c = 0 …(2)
Equation(1) is parallel to the given line so,
a(1) + b(-4) + c (7) = 0 …(3)
On solving eq(1), (2), and (3), we get
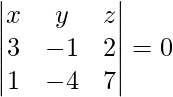
⇒ x – 19y – 11z = 0
Hence, the required equation of the plane is x – 19y – 11z = 0
Question 9. Find the vector and Cartesian equations of the line passing through (1, 2, 3) and parallel to the planes 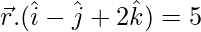 and
and 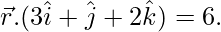
Solution:
Given that the equation of the line passing through (1, 2, 3) is
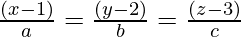 …(1)
…(1)
Here, the given line is parallel to plane x – y + 2z = 5
So, a × 1 + b × – 1 + c × 2 = 0
⇒ a – b + 2c = 0 …(3)
Also, the given line is parallel to plane 3x + y + z = 6
So, a × 3 + b × 1 + c × 1 = 0
⇒ 3a + b + c = 0 …(4)
On solving the equation (3) and (4) we get,
⇒ 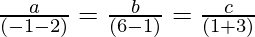
∴ a = – 3k, b = 5k and c = 4k
Now, put the value in the equation(1), we get
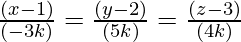
Now, multiplying by k we get
The required equation is 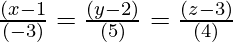
⇒ 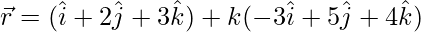
Hence, the equation of the plane is 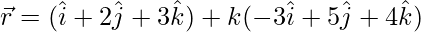
Question 10. Prove that the line of section of the plane 5x + 2y – 4z + 2 = 0 and 2x + 8y + 2z – 1 = 0 is parallel to the plane 4x – 2y – 5z – 2 = 0.
Solution:
Let us consider a, b and c be the direction ratios.
So,
⇒ a + 4b + c = 0
and, 5a + 2b – 4c = 0
On solving the above two equations, we get
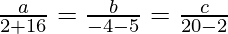
⇒ 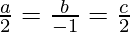
As we know that the line 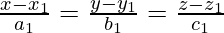 is parallel to plan a2x + b2y + c2z + d2 = 0, when a1a2 + b1b2 + c1c2 = 0
is parallel to plan a2x + b2y + c2z + d2 = 0, when a1a2 + b1b2 + c1c2 = 0
So, the line with direction ratio(a, b, c) is parallel to plane 4x – 2y – 5z – 2 = 0
aa1 + bb1 + cc1 = 0
2(4) + (-1)(-2) + (2)(-5) = 0
Hence proved that the line of section of the given plane is parallel to the given plane.
Question 11. Find the vector equation of the line passing through the point (1, -1, 2) and perpendicular to the plane 2x – y + 3z – 5 = 0.
Solution:
Let us consider a, b and c be the direction ratios.
Given that the equation of the line passing through the point (1, -1, 2)
So,
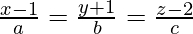 …..(1)
…..(1)
Also, the line is parallel to the normal of the plane.
⇒ 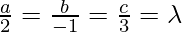
⇒ a = 2λ, b = -λ , c = 3λ
Now put all these values in eq(1), we get
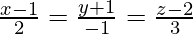
So, the line passes through a point whose position vector is 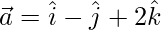 and parallel to
and parallel to 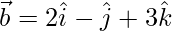
So, 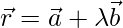
⇒ 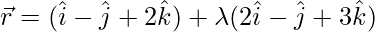 is the required equation.
is the required equation.
Question 12. Find the equation of the plane through the points (2, 2, -1) and (3, 4, 2) and parallel to the line whose direction ratios are 7, 0, 6.
Solution:
Given that the equation of the plane through the point (2, 2, -1)
a(x – 2) + b(y – 2) + c(z + 1) = 0 ….(1)
Also, the plane passes through points (3, 4, 2)
a(3 – 2) + b(4 – 2)+ c(2 + 1) = 0
or, a + 2b + 3c = 0 …(2)
As we know that the line 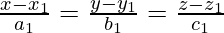 is parallel to plan a2x + b2y + c2z + d2 = 0, when a1a2 + b1b2 + c1c2 = 0
is parallel to plan a2x + b2y + c2z + d2 = 0, when a1a2 + b1b2 + c1c2 = 0
According to the question, the plane(1) is parallel to the line whose direction ratios are 7, 0, 6
So, 7a + 0b + 6c = 0 …(3)
Now, on solving the equation (1), (2), and (3), we have,
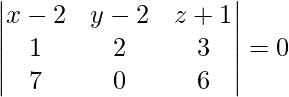
⇒ 12x + 15y – 14z – 68 = 0 is the required equation.
Question 13. Find the angle between the line 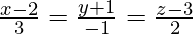 and the plane 3x + 4y + z + 5 = 0.
and the plane 3x + 4y + z + 5 = 0.
Solution:
Given that the equation of line is 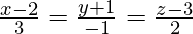 and the equation of the plane is 3x + 4y + z + 5 = 0
and the equation of the plane is 3x + 4y + z + 5 = 0
So, 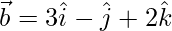
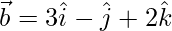
Angle between a line and a plane is
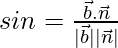
⇒ 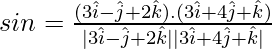
⇒ 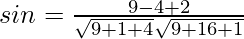
⇒ 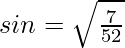
Thus, 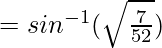
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...