Class 12 RD Sharma Solutions – Chapter 29 The Plane – Exercise 29.3 | Set 2
Last Updated :
19 Apr, 2021
Question 11. A plane passes through the point (1, -2, 5) and is perpendicular to the line joining the origin to the point (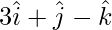 ). Find the vector and cartesian forms of the equation of the plane.
). Find the vector and cartesian forms of the equation of the plane.
Solution:
As we know that the vector equation of a plane passing through a point  and normal to
and normal to 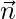 is
is
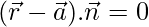 ….(i)
….(i)
Here, 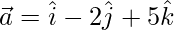
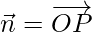
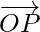 = Position vector of P – Position of vector of O
= Position vector of P – Position of vector of O
= 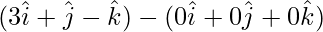
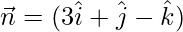
Now, put, all these values in equation (i), we get,
=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-71e3f006054f55a7232218e0df5f4927_l3.png)
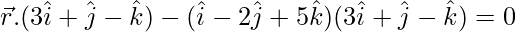
![Rendered by QuickLaTeX.com \vec{r}.(3\hat{i}+\hat{j}-\hat{k})-[(1)(3)+(-2)(1)+(5)(-1)]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0622a0fa7883e35dc8de90f92dfce48a_l3.png)
![Rendered by QuickLaTeX.com \vec{r}.(3\hat{i}+\hat{j}-\hat{k})-[3-2-5]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ddf9bd9427e06b3adcac56e5477650c1_l3.png)
![Rendered by QuickLaTeX.com \vec{r}.(3\hat{i}+\hat{j}-\hat{k})-[-4]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ef4388cf27fbc21d0a5f65924e2090e0_l3.png)
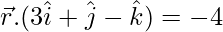 ….(2)
….(2)
Now put 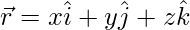 in eq(2), we get
in eq(2), we get

(x)(3) + (y)(1) + (z)(−1) = -4
3x + y − z = -4
So, this is the required equation of plane.
Question 12. Find the equation of the plane that bisects the line segment joining points (1, 2, 3) and (3, 4, 5) and is at right angle to it.
Solution:
As we know that the vector equation of a plane passing through a point  and normal to
and normal to 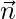 is
is
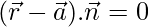 …..(i)
…..(i)
Here, 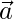 = mid-point of AB
= mid-point of AB
So, 
= Position vector of A + Position of vector of B/ 2
= 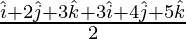
= 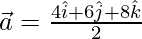

And, 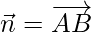
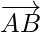 = Position vector of B – Position of vector of A
= Position vector of B – Position of vector of A
= 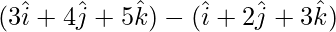
= 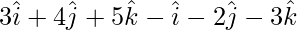

Now put all these values in eq(1), we get
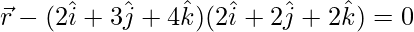
![Rendered by QuickLaTeX.com \vec{r}(2\hat{i}+2\hat{j}+2\hat{k})-[(2\hat{i}+3\hat{j}+4\hat{k})(2\hat{i}+2\hat{j}+2\hat{k})]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-74498af1605761ea23d0b4f1f3636b6e_l3.png)
![Rendered by QuickLaTeX.com \vec{r}(2\hat{i}+2\hat{j}+2\hat{k})-[(2)(2)+(3)(2)+(4)(2)]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b2006e46ccd7e2be4a14ad5745dafd99_l3.png)
![Rendered by QuickLaTeX.com \vec{r}(2\hat{i}+2\hat{j}+2\hat{k})-[4+6+8]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2bb7e59a04fab2d588a561fa7bc2346f_l3.png)
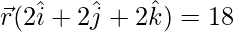 …..(2)
…..(2)
Now put 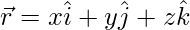 in eq(2), we get
in eq(2), we get

(x)(2) + (y)(2) + (z)(2) = 18
2x + 2y + 2z = 18
or we can write as
x + y + z = 9
So, this is the required equation of plane.
Question 13. Show that the normal to the following pairs of planes are perpendicular to each other:
(i) x – y + z – 2 = 0 and 3x + 2y – z + 4 = 0
Solution:
Given equations of planes are
x – y + z – 2 = 0 and 3x + 2y – z + 4 = 0
So first we solve, x – y + z – 2 = 0

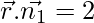 …..(i)
…..(i)
Now we solve, 3x + 2y – z =- 4

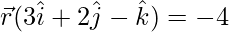
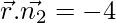 …(ii)
…(ii)
So, from eq(i) and (ii), we conclude that
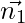 is normal to eq(i) and
is normal to eq(i) and 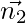 is normal to eq(ii)
is normal to eq(ii)
So,
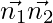 =
=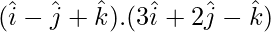
= (1)(3) + (-1)(2) + (1)(-1)
=3 – 2 – 1
= 3 – 3 = 0
Hence,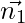 is perpendicular to
is perpendicular to 
(ii) 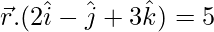 and
and 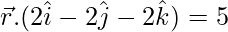
Solution:
Given equations of planes are
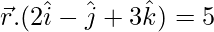 and
and 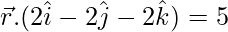
So first we solve, 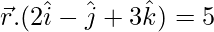
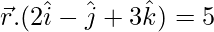
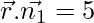 …..(1)
…..(1)
Now we solve, 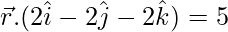
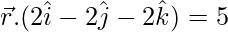
 ……(2)
……(2)
So, from eq(i) and (ii), we conclude that
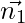 is normal to eq(i) and
is normal to eq(i) and 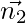 is normal to eq(ii)
is normal to eq(ii)
So,
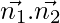 =
= 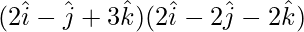
= (2)(2) + (-1)(-2) + (3)(-2)
= 4 + 2 – 6
= 6 – 6
= 0
Hence,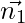 is perpendicular to
is perpendicular to 
Question 14. Show that the normal vector to the plane 2x + 2y + 2z = 3 is equally inclined with the coordinate axes.
Solution:
Equation of plane = 2x + 2y + 2z = 3
So,
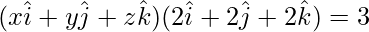
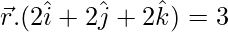
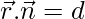
So, the normal to the plane 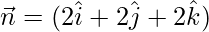
and the direction ratio of 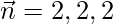
So, the direction cosine of 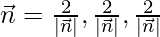 ….(1)
….(1)
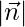 = √[(2)2 + (2)2 + (2)2]
= √[(2)2 + (2)2 + (2)2]
= √[4 + 4 + 4]
= √12 = 2√3
Now put the value of |\vec{n}| in eq(1), we get
Direction cosine of |\vec{n}| = 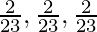
= 
So, u = 1/√3, v = 1/√3, W = 1/√3
Let us assume that the α, β, γ be the angle that normal \vec{n} makes with the coordinate axes.
So, u = cos α = 1/√3
α = cos-11/√3 ….(2)
v = cos β = 1/√3
β = cos-11/√3 ….(3)
w = cos γ = 1/√3
γ = cos-11/√3 ….(4)
So, from equation (2), (3) and (4), we get
α = β = γ
Hence proved that the normal vector to the plane 2x + 2y + 2z = 3 is equally inclined with the coordinate axes.
Question 15. Find a vector of magnitude 26 units normal to the plane 12x – 3y + 4y = 1.
Solution:
Given that,
The equation of plane is = 12x – 3y + 4y = 1
and the magnitude = 26 units
So,
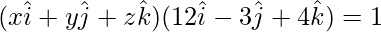
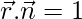
The normal to the plane is
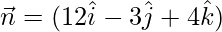
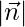 = √[(12)2 + (-3)2 + (4)2]
= √[(12)2 + (-3)2 + (4)2]
= √[144 + 9 + 16]
= √169 = 13
Hence, the unit vector 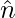 =
= 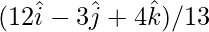
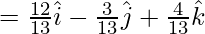
Now we find a vector normal to the plane with magnitude
So,
26 = 26 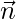
= 26 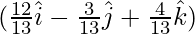
= 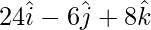
So, this is the required vector
Question 16. If the line drawn from (4, -1, 2) meets a plane at right angles at the point (-10, 5, 4), find the equation of the plane.
Solution:
As we know that the vector equation of a plane passing through a point  and normal to
and normal to 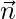 is
is
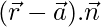 …..(i)
…..(i)
Here,  = position vector of B
= position vector of B
So, 
and 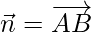
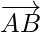 = Position vector of B – Position of vector of A
= Position vector of B – Position of vector of A
= 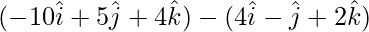
= 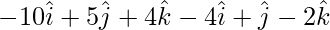
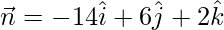
Now put all these values in eq(1), we get
![Rendered by QuickLaTeX.com [\vec{r}-(-10\hat{i}+5\hat{j}+4\hat{k})].(-14\hat{i}+6\hat{j}+2\hat{k})=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0af4a8cd48fe384ba779708a22d99358_l3.png)
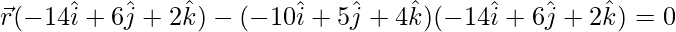
![Rendered by QuickLaTeX.com \vec{r}(-14\hat{i}+6\hat{j}+2\hat{k})-[(-10)(-14)+(5)(6)+(4)(2)]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9866b7149afdf3f18bceade6c24c8cae_l3.png)
![Rendered by QuickLaTeX.com \vec{r}(-14\hat{i}+6\hat{j}+2\hat{k})-[140+30+8]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c72d67557cc0902f6a0aa683568d825f_l3.png)
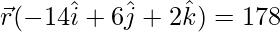 …..(2)
…..(2)
Now put 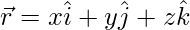 in eq(2), we get
in eq(2), we get
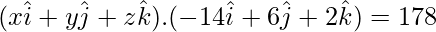
(x)(-14) + (y)(6) + (z)(2) = 178
-14x + 6y + 3z = 178
Or we can write as
7x – 2y – z = -89
So, this is the required equation of plane.
Question 17. Find the equation of the plane which bisects the line segment joining the points (-1, 2, 3) and (3, -5, 6) at right angles.
Solution:
Let assume that point (-1, 2, 3) is A point and point (3, -5, 6) is B point and C be the line mid-point of line segment AB
As we know that the vector equation of a plane passing through a point  and normal to
and normal to 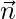 is
is
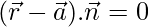 …(i)
…(i)
Here, 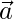 = Position vector of C
= Position vector of C
So, 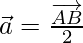 [Because c is the mid point of line AB]
[Because c is the mid point of line AB]
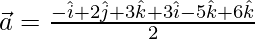
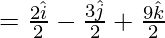
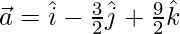
Now, 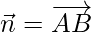
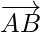 = Position vector of B- Position vector of A
= Position vector of B- Position vector of A
=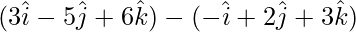
= 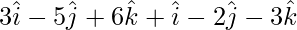
= 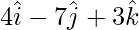
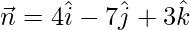
Now put all these values in eq(1), we get
=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-da5c837727a39a27e50d5d556f91b598_l3.png)
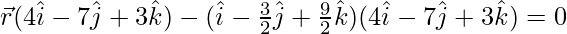
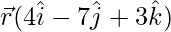 = 28 ….(2)
= 28 ….(2)
Now put 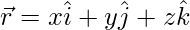 in eq(2), we get
in eq(2), we get

(x)(4) + (y)(-7) + (z)(3) = 28
4x – 7y + 3z = 28
So, this is the required equation of plane.
Question 18. Find the vector and cartesian equations of the plane which passes through the point (5, 2, -4) and perpendicular to the line with direction ratios 2, 3, -1.
Solution:
According to the given question
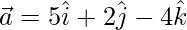
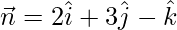
As we know that the vector equation of a plane passing through a point  and normal to
and normal to 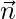 is
is
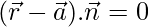
So,
![Rendered by QuickLaTeX.com [\vec{r}-(5\hat{i}+2\hat{j}-4\hat{k})].(2\hat{i}+3\hat{j}-\hat{k})=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-277092fb74f361e007bf590a83b38561_l3.png)
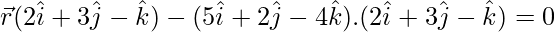
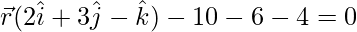
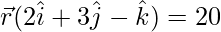 ….(1)
….(1)
For cartesian equation:
Put 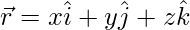 in eq(1), we get
in eq(1), we get
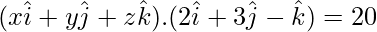
(x)(2) + (y)(3) + (z)(-1) = 20
2x + 3y -z = 20
So, this is the required equation of plane.
Question 19. If O be the origin and the coordinates of P be (1, 2, -3), then find the equation of the plane passing through P and perpendicular to OP.
Solution:
According to the question, a normal pass through point O(0, 0, 0) and P (1, 2, -3)
So, 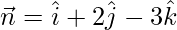
and 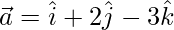
As we know that the vector equation of a plane passing through a point  and normal to
and normal to 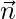 is
is
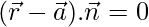
So,
![Rendered by QuickLaTeX.com [\vec{r}-(\hat{i}+2\hat{j}-3\hat{k})].(\hat{i}+2\hat{j}-3\hat{k})=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7d276ba3248e04443d16eb0ea8680310_l3.png)
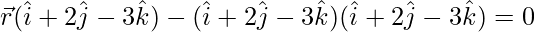
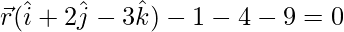
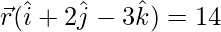
For cartesian equation:
Put 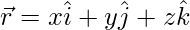 in eq(1), we get
in eq(1), we get
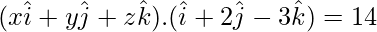
(x)(1) + (y)(2) + (z)(-3) = 14
x + 2y – 3z = 14
So, this is the required equation of plane.
Question 20. If O is the origin and the coordinates of A are (a, b, c). Find the direction cosines of OA and the equation of the plane through A at right angles to OA.
Solution:
According to the question it is given that, O is the origin and the coordinates of A are (a, b, c)
So, 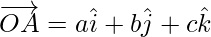
Since, the direction ratios of OA are proportional to a, b, c
So, the direction cosines are:
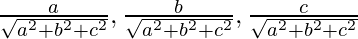
So the equation of the line is,
![Rendered by QuickLaTeX.com [(x\hat{i}+y\hat{j}+z\hat{k})-(a\hat{i}+b\hat{j}+c\hat{k})].(a\hat{i}+b\hat{j}+c\hat{k})=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-14b0767208bab6aa5b5b7e4b5daac528_l3.png)
ax + by + cz = a2 + b2 + c2
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...