Class 12 RD Sharma Solutions – Chapter 21 Areas of Bounded Regions – Exercise 21.3
Last Updated :
29 Mar, 2023
Question 1: Calculate the area of the region bounded by the parabolas y2 = 6x, x2 = 6y.
Solution:
Given,
y2 = 6x, x2 = 6y
y2 = 6x
⇒ y = √(6x)
x2 = 6y
⇒ y = √(x2/6)
Area of the region bounded by curve = Area under the curve y2=6x along x-axis – Area under the curve x2=6y along the x-axis
Required Area =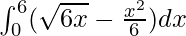
![Rendered by QuickLaTeX.com = [\frac{\sqrt{6}x^\frac{3}{2}}{\frac{3}{2}}-\frac{x^3}{18}]^6_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fa6c7699691cc590f81670c694b5b018_l3.png)
Putting the upper and lower limits we get,
Required Area = ![Rendered by QuickLaTeX.com [\frac{\sqrt{6}(6^\frac{3}{2})}{\frac{3}{2}}-\frac{6^3}{18}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e49a21d0647409d76f336800b648a788_l3.png)
![Rendered by QuickLaTeX.com =[\frac{2\times6^\frac{1}{2}(6^\frac{3}{2})}{3}-\frac{6^3}{18}] \\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-39dbd7590ea5c83866617b4abb4b3cd2_l3.png)
![Rendered by QuickLaTeX.com =[\frac{2\times6^2}{3}-\frac{6^3}{18}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-43eef2c1f7d40f22991c650291439145_l3.png)
= 24 – 12
= 12 sq. units
Question 2. Find the area of the region common to the parabolas 4y2 = 9x, 3x2 = 16y.
Solution:
Given,
4y2 = 9x, 3x2 = 16y
4y2 = 9x ⇒ y = √(9x/4)
3x2=16y ⇒ y = √(3x2/16)
Area of the region bounded by curve = Area under the curve 4y2=9x along x-axis – Area under the curve 3x2=16y along x-axis
Required area =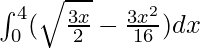
![Rendered by QuickLaTeX.com = [x^\frac{3}{2}-\frac{x^3}{16}]^4_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dd1fc6a6ddf6845b08097fe58c1d376b_l3.png) [Tex] [/Tex]
[Tex] [/Tex]
Putting the upper and lower limits we get,
Required Area = 43/2-43/16
= 8 – 64/16
= 4 sq. units
Question 3. Find the area of the region bounded by y=√x and x=y.
Solution:
Given,
y = √x, x = y
Area of the shaded region = Area under the curve along the x-axis – Area under the line along the x-axis
= 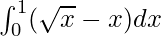
![Rendered by QuickLaTeX.com = [\frac{x^{3/2}}{3/2}-\frac{x^2}{2}]_0^1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0f7c0eab6b8a43df2f59a4795dd9c862_l3.png)
Putting the integration limits, we get:
Area of shaded region = ![Rendered by QuickLaTeX.com = [\frac{1^{3/2}}{3/2}-\frac{1^2}{2} - 0]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a570e131f5bbfa52757e34f3ac89054a_l3.png)
= 2/3 -1/2
= 1/6 sq. units
Question 4. Find the area bounded by the curve y=4-x2 and the lines y=0 and y=3.
Solution:
Given,
y = 4-x2, y = 0, y = 3
Area of shaded region = Area of region OCBEO + Area of region ODAEO
As the Y-axis divides the parabola into two symmetrical regions, the area of OCBEO = area of ODAEO
So,
Area of shaded region = 2 Area of ODAEO
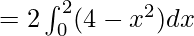
![Rendered by QuickLaTeX.com = 2[4x-x^3/3]^2_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-143670463868291f05eb15ac44388be8_l3.png)
Putting the limits, we get
Area of shaded region = 2[4(2)-2^3/3-0]
= 2[8-8/3]
= 32/3 sq. units
Question 5. Find the area of the region ![Rendered by QuickLaTeX.com [(x,y):\frac{x^2}{a^2}+\frac{y^2}{b^2}\leq 1 \leq \frac{x}{a}+\frac{y}{b}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-71dc36fb74bb2cfd1ead485ad285aaac_l3.png)
Solution:
Given
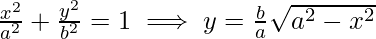
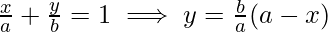
Area of shaded region = Area under the sector OAB – Area of triangle OAB
= 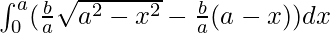
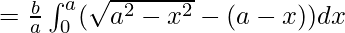
![Rendered by QuickLaTeX.com \frac{b}{a}[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}(\frac{x}{a})-ax+\frac{x^2}{2}]^a_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fdbaf50099d853cd17e6539f56819848_l3.png)
Putting the upper and lower limits, we get:
Area of shaded region = ![Rendered by QuickLaTeX.com \frac{b}{a}[\frac{a}{2}\sqrt{a^2-a^2}+\frac{a^2}{2}sin^{-1}(\frac{a}{a})-a(a)+\frac{a^2}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-008cd5f25c4e3871cb57356072b30a4c_l3.png)
![Rendered by QuickLaTeX.com =\frac{b}{a}[\frac{a}{2}*0+\frac{a^2}{2}(\frac{\pi}{2})-a^2+\frac{a^2}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0bf9c737fc3403d824b6187a07733a3b_l3.png)
![Rendered by QuickLaTeX.com =\frac{b}{a}[\frac{a^2\pi}{4}-\frac{a^2}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-341f2dd1708181585c3d3aaf4fcc8ed7_l3.png)
![Rendered by QuickLaTeX.com = \frac{b}{a}[\frac{a^2\pi}{4}-\frac{a^2}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bb359047f208edcf73a0d73b7a9bfdfe_l3.png)
![Rendered by QuickLaTeX.com = \frac{b}{a}*a^2[\frac{\pi}{4}-\frac{1}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d31a82ac2d8cfb13fbec99e7f1d54757_l3.png)
![Rendered by QuickLaTeX.com =\frac{ab}{4}[\pi-2] sq. units](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-018d7d54747655a3609484e5ad6a949b_l3.png)
Question 6. Using integration, find the area of the region bounded by the triangle whose vertices are (2,1), (3,4), and (5,2).
Solution:
Given, A(2,1), B(3,4) and C(5,2). We need to find the area of triangle ABC. To calculate the area we need to find the equations of the lines AB, BC, and CA.
The equation of a line can be calculated as:
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9cc2ce5f81e144a1e90bc7d3f8bc4230_l3.png)
Equation of AB:
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8eee073f130fc9fc335c52d451b7a7ff_l3.png)
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a684f23971b72aded01fa53dfbb7deb4_l3.png)
y-1 = 3x-6 ⇒ y=3x-5
Equation of BC:
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b2027e397f64c83dda7c61800931b2ea_l3.png)
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b96cefc1e3f9a79a57377532b50ed919_l3.png)
y-4= -x+3 ⇒ y=-x+7
Equation of CA:
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f01aae259c5ee32ebd0d2e51badbb858_l3.png)
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d9a716390cbe209a1083e6352544b6c0_l3.png)
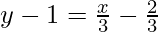
y = x/3 + 1/3 ⇒ 3y = x+1
Required Area = Area of Region I + Area of Region II………………(1)
Area of Region I = Area under AB from x=2 to x=3 – Area under AC from x=2 to x=3
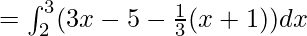
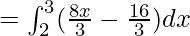
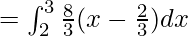
![Rendered by QuickLaTeX.com =\frac{8}{3}[\frac{x^2}{2}-2x]^3_2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-64196e88545f23a4f0746873877eada4_l3.png)
![Rendered by QuickLaTeX.com =\frac{8}{3}[\frac{3^2}{2}-2*3 -\frac{2^2}{2}+2*2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f4f817e877d243c62a4c4b4b7f96051a_l3.png)
![Rendered by QuickLaTeX.com = \frac{8}{3}[\frac{9-4}{2}-2(3-2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-da67ae1656a706718fecf5ca2a03a929_l3.png)
![Rendered by QuickLaTeX.com = \frac{8}{3}[\frac{5}{2}-2] = \frac{4}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c6483b16000214a2a002f8a31cba1c36_l3.png)
Area of Region I = 4/3 sq. units …………………(2)
Area of Region II = Area under BC from x=3 to x=5 – Area under AC from x=3 to x=5
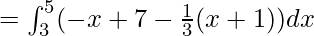
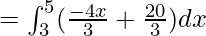
![Rendered by QuickLaTeX.com =[\frac{-4x^2}{6}+\frac{20x}{3}]^5_3](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ffd74a0f5aa4550793d68f2065bf518a_l3.png)
![Rendered by QuickLaTeX.com = [\frac{-100}{6}+\frac{100}{3}-(\frac{-36}{6}+\frac{60}{3})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-adf3f8d090f83a5ab60052fc9c7a3f78_l3.png)
= 8/3 sq. units
Area of Region II = 8/3 sq. units ……………………….(3)
Putting the value of (2) and (3) in (1), we get:
Required Area = Area of region I + Area of region II
= 4/3 + 8/3 = 4 sq. units
Question 7. Using integration, find the area of the region bounded by the triangle whose vertices A, B, and C are (-1,1), (0,5), and (3,2).
Solution:
Given, A (2,1), B (3,4) and C (5,2). We need to find the area of triangle ABC. To calculate the area we need to find the equations of the lines AB, BC, and CA.
The equation of a line can be calculated as:
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9cc2ce5f81e144a1e90bc7d3f8bc4230_l3.png)
Equation of AB:
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e056aa6e72a901f4ded108cdf1dce6f5_l3.png)
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e7b9da68971b66b99d2d4b52f68ff947_l3.png)
y-1 = 4x+4
y = 4x+5
Equation of BC:
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-18561baf0de361b2c9f92fd8a1627331_l3.png)
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1d1de7190d5ec2de5fd3ea06b33d51de_l3.png)
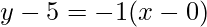
y-5= -x
y = -x+5
Equation of CA
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bf38b16483c30ef824cf0e133e2994f3_l3.png)
](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-88c7939e33bc2be02272338c84d4a413_l3.png)
![Rendered by QuickLaTeX.com y-1=[\frac{x}{4}+\frac{1}{4}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a24f93648a51bedcefe01ae26960f51b_l3.png)
y = x/4 + 5/4
4y = x+5
Required Area = Area of Region I + Area of Region II ………………(1)
Area of Region I = Area under AB from x=-1 to x=0 – Area under AC from x=-1 to x=0
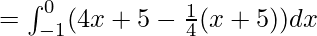
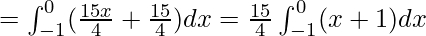
![Rendered by QuickLaTeX.com = \frac{15}{4}[\frac{x^2}{2}+x]_{-1}^0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6cfe3f506a27ef46e06bd117d96dc72b_l3.png)
![Rendered by QuickLaTeX.com = \frac{15}{4}[0-(\frac{1}{2}-1)] = \frac{15}{8}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-016704de02aa9f6788147d099e150bb9_l3.png)
Area of Region I = 15/8 sq. units …………………(2)
Area of Region II = Area under BC from x=0 to x=3 – Area under AC from x=0 to x=3
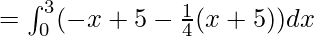
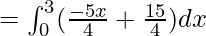
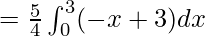
![Rendered by QuickLaTeX.com = \frac{5}{4}[\frac{-x^2}{2}+3x]^3_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-40681956783e8135fbe81af9aaa33463_l3.png)
![Rendered by QuickLaTeX.com \frac{5}{4}[\frac{-3^2}{2}+3(3)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fafe2cc63035f3dbc9a5461baa417e16_l3.png)
![Rendered by QuickLaTeX.com = \frac{5}{4}[\frac{-9}{2}+9-(0)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6fa1ad191ab9de4cc6ccbc350f7ae50e_l3.png)
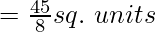
Area of Region II = 45/8 sq. units ……………………….(3)
Putting the value of (2) and (3) in (1), we get:
Required Area = 15/8+ 45/8
= 15/2 sq. units
Question 8. Using integration, find the area of triangular the region, the equations of whose sides are y = 2x+1, y = 3x+1, and x = 4.
Solution:
Area of the shaded region in the above graph can be calculated as:
Required area = Area under line y=3x+1 from x=0 to x=4 – Area under the line y=2x+1 from x=0 to x=4
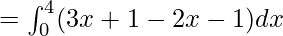
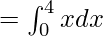
![Rendered by QuickLaTeX.com = [\frac{x^2}{2}]^4_0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-062e908466957a1cdd8d8c3ec9338517_l3.png)
![Rendered by QuickLaTeX.com = [\frac{4^2}{2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dfdf891ffdbeb7510100e16a1b88d0d0_l3.png)
= 8 sq. units
Question 9. (x – a)2 + (y – b)2 = r2. Find the area of the region {(x, y): y2≤8x, x2+y2≤9}
Solution:
Given,
y2 = 8x ⇒ y = √8x
x2 + y2=9 ⇒ y = √(9-x2)
As the circle is divided by the parabola into two symmetrical halves,
Area of the shaded region = 2(Area under the parabola y2=8x from x=0 to x=1 + Area under the circle x2+y2=9 from x = 1 to x = 3)
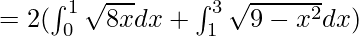
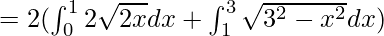
![Rendered by QuickLaTeX.com = 2([\frac{2\sqrt{2}x^\frac{3}{2}}{3/2}]^1_0 + [\frac{x}{2}\sqrt{9-x^2}+\frac{9}{2}sin^{-1}(\frac{x}{3})]^3_1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f68e5964b6aa81fd607c9db5de93a749_l3.png)
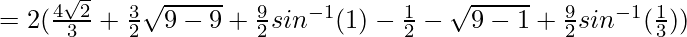
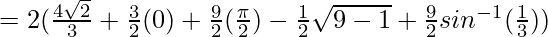
![Rendered by QuickLaTeX.com = 2[\frac{4\sqrt{2}}{3}+\frac{9\pi}{4}-\sqrt{2}-\frac{9}{2}sin^{-1}(\frac{1}{3})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e589e60a492a668b891289158f422c08_l3.png)
Required Area ![Rendered by QuickLaTeX.com = 2[\frac{\sqrt{2}}{3}+\frac{9\pi}{4}-\frac{9}{2}sin^{-1}(\frac{1}{3})]~sq.~units](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c49ba304d40fd7b6f99524ea3f708849_l3.png)
Question 10. Find the area of the region bounded by the circle x2+y2=16 and the parabola y2=6x.
Solution:
Given
y2 = 6x ⇒ y = √6x
x2 + y2=16 ⇒ y = √(16-x2)
As the circle is divided by the parabola into two symmetrical halves,
Area of the shaded region = 2(Area under the parabola y2=6x from x=0 to x=2 + Area under the circle x2+y2=16 from x = 2 to x = 4)
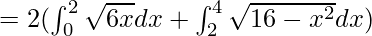
![Rendered by QuickLaTeX.com = 2([\frac{\sqrt{6}x^\frac{3}{2}}{3/2}]^2_0 + [\frac{x}{2}\sqrt{16-x^2}+\frac{16}{2}sin^{-1}(\frac{x}{4})]^2_4)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-761bda2858da494043d4fe750ad3d947_l3.png)
![Rendered by QuickLaTeX.com = 2([\frac{\sqrt{6}x^\frac{3}{2}}{3/2}]^2_0 + [\frac{x}{2}\sqrt{16-x^2}+8sin^{-1}(\frac{x}{4})]^2_4)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d7727571d727de33f8a3b6287a6b71f7_l3.png)
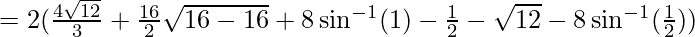
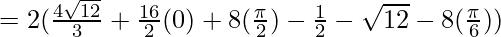
![Rendered by QuickLaTeX.com = 2[\frac{8\sqrt{3}}{3}+4\pi-2\sqrt{3}-\frac{4\pi}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ae5af66aefb005539cbf380b37933956_l3.png)
![Rendered by QuickLaTeX.com = 2[\frac{2\sqrt{3}}{3}+\frac{8\pi}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-95cbe133ff1a059c4ff6b0a45bfecb0a_l3.png)
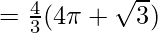
Required Area = 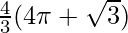 sq.units
sq.units
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...