Class 12 RD Sharma Solutions – Chapter 21 Areas of Bounded Regions – Exercise 21.2
Last Updated :
21 Feb, 2021
Question 1. Find the area in the first quadrant bounded by the parabola y = 4x2 and the lines x = 0, y = 1, and y = 4.
Solution:
From the question it is given that,
Lines, x = 0, y = 1, y = 4
Parabola y = 4x2 … [equation (i)]
So, equation (i) represents a parabola with vertex (0, 0) and axis as y – axis. x = 0 is y – axis and y = 1, y = 4 are line parallel to x – axis passing through (0, 1) and (0, 4) respectively, as shown in the rough sketch below,
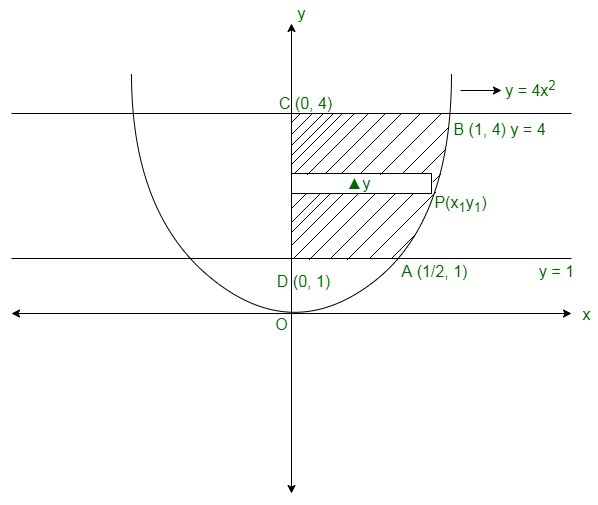
Now, we have to find the area of ABCDA,
Then, the area can be found by taking a small slice in each region of width Δy,
And length = x
The area of sliced part will be as it is a rectangle = x Δy
So, this rectangle can move horizontal from y = 1 to x = 4
The required area of the region bounded between the lines = Region ABCDA
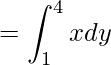
Given, y = 4x2
x = 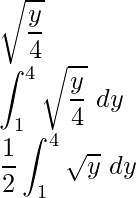
On integration, we get,
![Rendered by QuickLaTeX.com \displaystyle=\frac{1}{2}\left[\frac{2}{3}y\sqrt y\right]_1^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7a5afc58e19f78b018a689d2132e4b17_l3.png)
Now, applying limits we get,
![Rendered by QuickLaTeX.com = \frac{1}{2} \left[\left(\frac{2}{3} × 4 × \sqrt4\right) - \left(\frac{2}{3} × 1 × \sqrt1\right)\right]\\ = \frac{1}{2} \left[\frac{16}{3} - \frac{2}{3}\right]\\ = \frac{1}{2} \left[\frac{(16 - 2)}{3}\right]\\ = \frac{1}{2} \left[\frac{14}{3}\right]\\ = \frac{7}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-98a7159906bf2788bf40acf35d407d25_l3.png)
Therefore, the required area is 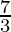 square units.
square units.
Question 2. Find the area of the region bounded by x2 = 16y, y = 1, y = 4, and the y-axis in the quadrant.
Solution:
From the question it is given that,
Region in first quadrant bounded by y = 1, y = 4
Parabola x2 = 16y … [equation (i)]
So, equation (i) represents a parabola with vertex (0, 0) and axis as y-axis, as shown in the rough sketch below,

Now, we have to find the area of ABCDA,
Then, the area can be found by taking a small slice in each region of width Δy,
And length = x
The area of sliced part will be as it is a rectangle = x Δy
So, this rectangle can move horizontal from y = 1 to x = 4
The required area of the region bounded between the lines = Region ABCDA
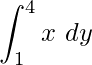
Given, x2 = 16y
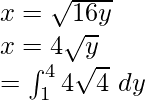
On integrating we get,
![Rendered by QuickLaTeX.com =4\left[\frac{2}{3}y\sqrt y\right]^4_1\\ =\int_1^4x\ dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3b6b87e68589ec7e06420c007febf5e7_l3.png)
Given, x2 = 16y
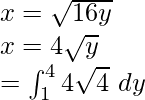
On integrating we get,
![Rendered by QuickLaTeX.com =4\left[\frac{2}{3}y\sqrt y\right]^4_1\\ =\int_1^4x\ dy](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3b6b87e68589ec7e06420c007febf5e7_l3.png)
Now, applying limits we get,
![Rendered by QuickLaTeX.com = 4 \left[\left(\frac{2}{3} × 4 × \sqrt4\right) - \left(\frac{2}{3}× 1 × \sqrt1\right)\right]\\ = 4 \left[\frac{16}{3} - \frac{2}{3}\right]\\ = 4 \left[\frac{(16 - 2)}{3}\right]\\ = 4 \left[\frac{14}{3}\right]\\ = \frac{56}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3738bb7a37d008697bbe4e3c7d74bede_l3.png)
Therefore, the required area is 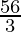 square units.
square units.
Question 3. Find the area of the region bounded by x2 = 4ay and its latus rectum.
Solution:
We have to find the area of the region bounded by x2 = 4ay

Then,
Area of the region = 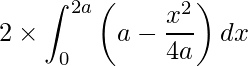
On integrating we get,
= ![Rendered by QuickLaTeX.com 2\times\left[ax-\frac{x^3}{12a}\right]_0^{2a}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2800dc6fde0898bf4e28911ab3b6cf04_l3.png)
Now applying limits,
![Rendered by QuickLaTeX.com = 2 × \left[(a (2a - 0)) - \frac{((2a)^3 - 0^3)}{12a}\right]\\ = 2 × \left[(2a^2) - \frac{8a^3}{12a}\right]\\ = 2 × \left[\frac{(24a^3 - 8a^3)}{12a}\right]\\ = 2 × \left[\frac{16a^3}{12a}\right]\\ = 2 × \left[\frac{4a^2}{3}\right]\\ = \frac{8a^2}{3}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-501b64a856ac050d3c4b420bcb3f6878_l3.png)
Therefore, the area of the region is 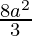 square units.
square units.
Question 4. Find the area of the region bounded by x2 + 16y = 0 and its latus rectum.
Solution:
We have to find the area of the region bounded by x2 + 16y = 0

Then,
Area of the region = ![Rendered by QuickLaTeX.com \displaystyle2\times\int_0^{8}\left[-\frac{x^2}{16}-(-4)\right]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-926b33bbe17722397fbc082ad47ec1e5_l3.png)
On integrating we get,
= ![Rendered by QuickLaTeX.com 2\times\left[4x-\frac{x^3}{48}\right]_0^{8}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-26d059a045da0dcb616a845c3befc9b9_l3.png)
Now applying limits,
![Rendered by QuickLaTeX.com = 2 × \left[(4 (8 - 0)) - \frac{((8)^3 - 0^3)}{48}\right]\\ = 2 × \left[(32) - \frac{512}{48}\right]\\ = 2 × \left[(32)-\frac{32}{3}\right]\\ = 2 × \left[\frac{96-32}{3}\right]\\ = 2 × \left[\frac{64}{3}\right]\\ = \frac{128}{3}\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-91d107eabe397fc95b86254c06b0cad6_l3.png)
Therefore, the area of the region is 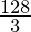 square units.
square units.
Question 5. Find the area of the region bounded by the curve ay2 = x3, the y-axis, and the lines y = a and y = 2a.
Solution:
We have to find the area of the region bounded by curve ay2 = x3, and lines y = a and y = 2a.

Then,
Area of the region = 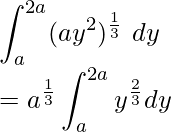
On integrating we get, = ![Rendered by QuickLaTeX.com a^{\frac{1}{3}}\left[\frac{3}{5}y^{\frac{5}{3}}\right]_0^{2a}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8aad58308b56da81234acb5891bcd1ba_l3.png)
Now applying limits we get, = 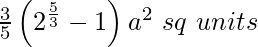
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...