Class 12 RD Sharma Solutions – Chapter 19 Indefinite Integrals – Exercise 19.3 | Set 2
Last Updated :
03 Mar, 2021
Question 11. Integrate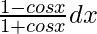
Solution:
Let I =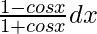
On simplifying the above equation, we get
I = 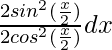
= 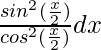
= ∫ tan2 x/2 dx
= 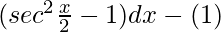
On integrating the equation(1), we get
= 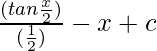
Hence, I = 2 tan x/2 – x + c
Question 12. Integrate 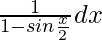
Solution:
Let I = 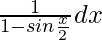
Now multiply with the conjugate,
= 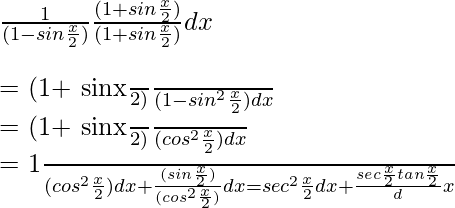
On integrating the equation, we get
= 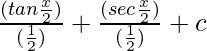
= 2 tan x/2 + 2 sec x/2 +c
Hence, I = 2 (tan x/2 + sec x/2) + c
Question 13. Integrate 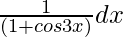
Solution:
Let I = 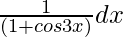
Now multiply with the conjugate,
= ∫ 1/(1 + cos 3x) × (1 – cos 3x)/(1 – cos 3x) dx
= ∫ (1 – cos 3x)/ (1 – cos2 3x) dx
= ∫ (1 – cos 3x)/ (sin2 3x) dx
= ∫ (1/ sin2 3x) – (cos 3x/ sin2 3x) dx
= ∫ (cosec2 3x – cosec3x cot3x) dx -(1)
On integrating the equation(1), we get
= – cot 3x/3 + cosec 3x/3 + c
= (-1/3) × (cos 3x/ sin 3x) + (1/3) × (1/sin 3x) + c
= (1 – cos 3x) / 3 sin 3x + c
Therefore, I = (1 – cos 3x) / 3 sin 3x + c
Question 14. Integrate ∫(ex + 1)2 ex dx
Solution:
Let I = ∫ (ex + 1)2 ex dx -(1)
(ex + 1) = t -(2)
On differentiating the above equation, we get
ex dx = dt -(3)
Now, put the eq(2) and (3) in eq(1)
= ∫ (t2) dt -(4)
On integrating the equation(4), we get
= (t3 /3) + c
Therefore, I = (ex + 1)3 /3 + c
Question 15. Integrate ∫ (ex + (1 + ex))2 dx
Solution:
Let I = ∫ (ex + (1/ex))2 dx
= ∫ (e2x + (1/e2x) + 2)dx -(1)
On integrating the equation(1), we get
= (e2x/2) – (1/2 e-2x) + 2x + c
Therefore, I = (e2x/2) – (1/2 e-2x) + 2x + c
Question 16. Integrate 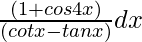
Solution:
Let I = 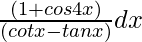
= 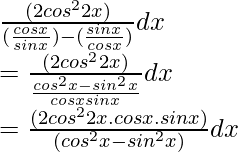
On simplifying the above equation,
= ∫ cos22x. (sin2x / cos2x) dx
= ∫ cos 2x. sin2x dx
= 1/2∫ sin (2x + 2x) + sin (2x – 2x) dx
= 1/2∫(sin 4x + sin 0) dx
= 1/2∫(sin 4x + 0) dx
= 1/2 ∫sin 4x dx -(1)
On integrating the equation(1), we get
= (-1/2) ((cos 4x)/4) + c
Therefore, I = (-1/8) (cos 4x) + c
Question 17. Integrate 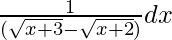
Solution:
Let I = 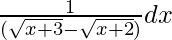
Now multiply with the conjugate,
= 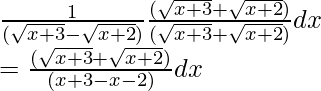
= ∫(x +3)1/2 + (x + 2)1/2 dx -(1)
On integrating the equation(1), we get
= 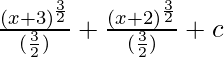
= (2/3)(x + 3)3/2 +(2/3) (x + 2)3/2 + c
Hence, I = (2/3){(x + 3)3/2 + (x + 2)3/2} +c
Question 18. Integrate ∫ tan2(2x – 3) dx
Solution:
Let I = ∫ tan2(2x – 3) dx
= ∫ sec2 (2x – 3) – 1 dx -(1)
Now put, 2x – 3 = t -(2)
2dx = dt -(3)
Put eq(3) and (2) in eq(1)
= 1/2∫sec2 t dt – ∫1dx -(4)
On integrating the equation(4), we get
= 1/2 tan t – x + c
= 1/2 tan(2x – 3) – x + c
Therefore, I = 1/2 tan(2x – 3) – x + c
Question 19. Integrate 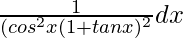
Solution:
Let I = 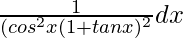
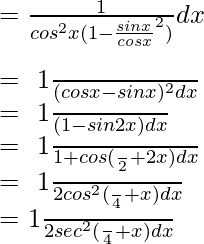
On integrating the equation, we get
= 1/2 tan(π/4 + x) + c
Therefore, I = 1/2 tan(π/4 + x) + c
Share your thoughts in the comments
Please Login to comment...