Question 25. Evaluate ∫(tanx + cotx)2 dx
Solution:
We have, ∫(tanx + cotx)2 dx
By using formula (x + y)2 = x2 + y2 + 2xy
We get, ∫(tan2x + cot2x + 2tanx cotx)dx
= ∫ (sec2x – 1 + cosec2x – 1 + ((2 × 1)/cotx) × cotx)dx
= ∫ (sec2x + cosec2x)dx
= ∫sec2xdx + ∫cosec2xdx
= tanx – cotx + c
Question 26. Evaluate ∫(1 – cos2x)/(1 + cos2x) dx
Solution:
We have, ∫(1 – cos2x)/(1 + cos2x) dx
= ∫(2sin2x)/(2cos2x) dx
= ∫tan2xdx
= ∫(sec2x – 1)dx
= ∫sec2xdx – 1∫dx
= tanx – x + c
Question 27. Evaluate ∫(cosx)/(1 – cosx) dx
Solution:
We have, ∫(cosx)/(1 – cosx) dx
= ∫(cosx(1 + cosx))/((1 – cosx)(1 + cosx)) dx
= ∫(cosx + cos2x)/(1 – cos2x) dx
= ∫(cosx + cos2x)/(sin2x) dx
= ∫(cosx)/(sin2x) dx + ∫(cos2x)/(sin2x) dx [Since, cosx/sinx = cotx]
= ∫cotx × cosecxdx + ∫(cosec2x – 1)dx [Since, cot2x = cosec2x – 1]
= -cosecx – cotx – x + c
Question 28. Evaluate ∫cos2x – sin2x/√(1 + cos4x) dx
Solution:
We have, ∫cos2x – sin2x/√(1 + cos4x) dx
= ∫(cos2x – sin2x)/√(2cos22x) dx
= 1/√2 ∫(cos2x – sin2x)/(cos2x) dx
= 1/√2∣(cos2x – sin2x)/(cos2x – sin2x) dx
= 1/√2∫1 × dx
= x/√2 + c
Question 29. Evaluate ∫ 1/(1 – cosx) dx
Solution:
We have, ∫ 1/(1 – cosx) dx
= ∫1/(1 – cosx) × (1 + cosx)/(1 + cosx) × dx
= ∫(1 + cosx)/(1 – cos2x) × dx
= ∫(1 + cosx)/(sin2x) × dx
= ∫1/(sin2x) dx + ∫(cosx)/(sin22x) dx
= ∫cosec2xdx + ∫cotx × cosecx dx
= -cotx – cosecx + c
Question 30. Evaluate ∫1/(1 – sinx) dx
Solution:
We have, ∫1/(1 – sinx) dx
= ∫1/(1 – sinx) × (1 + sinx)/(1 + sinx) × dx
= ∫(1 + sinx)/(1 – sin2x) × dx
= ∫(1 + sinx)/(cos2x) × dx
= ∫(1/(cos2x) + (sinx)/(cos2x)) × dx
= ∫1/(cos2x) dx + ∫(sinx)/(cos2x) × dx
= ∫sec2xdx + ∫tanx secx dx
= tanx + secx + c
Question 31. Evaluate ∫(tanx)/(secx + tanx) dx
Solution:
We have, ∫(tanx)/(secx + tanx) dx
= ∫(tanx)/(secx + tanx) × (secx – tanx)/(secx – tanx) × dx
= ∫(tanx(secx – tanx))/(sec2x – tan2x) × dx
= ∫(tanxsecx – tan2x)dx
= ∫sectanxdx – ∫(sec2x – 1)dx
= ∫secxtanxdx – ∫sec2xdx + 1∫dx
= secx – tanx + x + c
Question 32. Evaluate ∫(cosecx)/(cosecx – cotx)dx
Solution:
We have, ∫(cosecx)/(cosecx – cotx)dx
= ∫(cosecx)/(cosecx – cotx) × (cosecx + cotx)/(cosecx + cotx) × dx
= ∫(cosecx(cosecx + cotx))/(cosec2x – cot2x) × dx
= ∫(cosec2x + cosecx cotx)dx
= ∫cosec2xdx + ∫cosecx cotx dx
= -cotx – cosecx + c
Question 33. Evaluate ∫1/(1 + cos2x) dx
Solution:
We have, ∫1/(1 + cos2x) dx
= ∫ 1/(2cos2x) × dx
= 1/2 ∫sec2x × dx
= 1/2 × tanx + c
= (tanx)/2 + c
Question 34. Evaluate∫1/(1 – cos2x) dx
Solution:
We have, ∫1/(1 – cos2x) dx
= ∫1/(2sin2x)dx
= 1/2 ∫cosec2x dx
= (-1)/2 × cotx + c
= (-cotx)/2 + c
Question 35. Evaluate ∫tan-1[(sin2x)/(1 + cos2x)]dx
Solution:
We have, ∫tan-1[(sin2x)/(1 + cos2x)]dx
= ∫tan-1[(2sinxcosx)/(2cos2x)]dx
= ∫tan-1[(sinx)/(cosx)]dx
= ∫tan-1(tanx)dx
= ∫xdx
= x2/2 + c
Question 36. Evaluate ∫cos-1(sinx)dx
Solution:
We have, ∫cos-1(sinx)dx
= ∫cos-1[cos(π/2 – x)]dx
= ∫(π/2 – x)dx
= π/2 ∫dx – ∫xdx
= π/2 × x – x2/2 + c
Question 37. Evaluate ∫ cot-1(sinx)dx
Solution:
We have, ∫ cot-1(sinx)dx
= ∫cot-1[(sin2x)/(1 – cos2x)]dx
= ∫cot-1((cosx)/(sinx))dx
= ∫cot-1(cotx)dx
= ∫xdx
= x2/2 + c
Question 38. Evaluate ∫ sin-1((2tanx)/(1 + tan2x))dx
Solution:
We have, ∫ sin-1((2tanx)/(1 + tan2x))dx
= ∫ sin-1(sin2x)dx
= ∫2xdx
= 2∫xdx
= (2x2)/2 + c
= x2 + c
Question 39. Evaluate ∫((x3 + 8)(x – 1))/(x2 – 2x + 4) dx
Solution:
We have, ∫((x3 + 8)(x – 1))/(x2 – 2x + 4) dx
= ∫((x + 2)(x2 – 2x + 4)(x – 1))/(x2 – 2x + 4) dx
= ∫(x + 2)(x – 1)dx
= ∫(x2 – x+2x – 2)dx
= ∫(x2 + x – 2)dx
= x3/3 + x2/2 – 2x + c
Question 40. Evaluate ∫(atanx + bcotx)2 dx
Solution:
We have, ∫(atanx + bcotx)2 dx
By using formula (x + y)2 = x2 + y2 + 2xy , we get
= ∫(a2 tan2x + b2cot2x + 2ab tanx cotx)dx
= ∫[a2 (sec2x – 1) + b2(cosec2x – 1) + 2ab]dx
= ∫[a2 sec2x – a2 + b2cosec2x – b2 + 2ab]dx
= a2tanx – a2x – b2 cotx – b2x + 2abx + c
= a2tanx – b2 cotx – (a2 + b2 – 2ab)x + c
Question 41. Evaluate ∫(x3 – 3x2 + 5x – 7 + x2 ax)/(2x2) dx
Solution:
We have, ∫(x3 – 3x2 + 5x – 7 + x2 ax)/(2x2) dx
= 1/2 ∫x3/x2dx – 3/2∫x2/x2dx + 5/2∫x/x2dx – 7/2∫x-2dx + 1/2∫(x2ax)/x2dx
= 1/2 × x2/2 – 3/2x + 5/2 logx – 7/2 x-1 + 1/2ax/(loga) + c
= 1/2 [x2/2 – 3x + 5logx + 7/x + ax/(loga)] + c
Question 42. Evaluate ∫cosx/(1 + cosx) dx
Solution:
We have, ∫cosx/(1 + cosx) dx …..(1)
Now solve
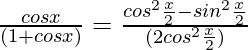
Since, cosx = cos2x/2 – sin2x/2 and cosx + 1 = 2cos2x/2
So, we get cosx/(1 + cosx) = 1/2[1 – tan2x/2]
Now put this value in eq(1), we get
= 1/2 ∫(1 – tan2x/2)dx
= 1/2 ∫(1 – sec2x/2 + 1)dx
= 1/2 ∫(2 – sec2x/2)dx
= 1/2 [2x – (tanx/2)/(1/2)] + c
= x – tanx/2 + c
Question 43. Evaluate∫(1 – cosx)/(1 + cosx) dx
Solution:
We have, ∫(1 – cosx)/(1 + cosx) dx ….(1)
Now solve
(1 – cosx)/(1 + cosx) = (2sin2x)/(2cos2x)
= tan2x/2
= (sec2x/2 – 1) [Since, 2sin2x/2 = 1 – cosx and 2cos2x/2 = 1 + cosx]
Now put this value in eq(1), we get
= ∫(sec2x/2 – 1)dx
= tan(x/2)/(1/2) – x + c
= 2tanx/2 – x + c
Question 44. Evaluate ∫{3sinx – 4cosx + 5/(cos2x) – 6/(sin2x) + tan2x – cot2x}dx
Solution:
We have, ∫{3sinx – 4cosx + 5/(cos2x) – 6/(sin2x) + tan2x – cot2x}dx
= 3∫sinxdx – 4∫cosxdx + 5∫sec2dx – 6∫cosec2x + ∫tan2xdx – ∫cot2xdx
= 3∫sinxdx – 4∫cosxdx + 5∫sec2xdx – 6∫cosec2x + ∫(sec2x – 1)dx – ∫(cosec2x – 1)dx
= 3∫sinxdx – 4∫cosxdx + 6∫sec2xdx – 7∫cosec2xdx
= -3cosx – 4sinx + 6tanx + 7cotx + c
Question 45. If f'(x) = x – 1/x2 and f(1) = 1/2, find f(x)?
Solution:
Given that ∫f'(x) = x – 1/x2
and f(1) = 1/2
We have to find f(x)
So, ∫f'(x) = ∫xdx – ∫1/x2dx
f(x) = x2/2 + x-1 + c
f(x) = x2/2 + 1/x + c
f(x) = x2/2 + 1/x + c …..(i)
As we know that
f(1) = 1/2
12/2 + 1/1 + c = 1/2
1/2 + 1 + c = 1/2
c = -1
On putting c = -1 in (i), we get
f(x) = x2/2 + 1/x – 1
Question 46. If f'(x) = x + b, f(1) = 5, f(2) = 13, find f(x)?
Solution:
Given that f'(x) = x + b
and f(1) = 5, f(2) = 13
We have to find f(x)
So, ∫f'(x) = ∫(x + b)dx
f(x) = x2/2 + bx + c …….(i)
As we know that
f(1) = 5
12/2 + b × 1 + c = 5
1/2 + b + c = 5
b + c = 9/2 …….(ii)
Also, f(2) = 13
22/2 + b × 2 + c = 13
2 + 2b + c = 13
2b + c = 11 …….(iii)
Now, subtract eq(ii) from eq(iii), we get
b = 11 – 9/2
b = 13/2
Now, put b = 13/2 in eq(ii), we get
13/2 + c = 9/2
c = 9/2 – 13/2
c = (9 – 13)/2
= (-4)/2
= -2
Now, on putting b = 13/2 and c = -2 in equation (i), we get
f(x) = x2/x + 13/2x – 2
f(x) = x2/2 + 13/2x – 2
Question 47. If f'(x) = 8x3 – 2x, f(2) = 8, find f(x)?
Solution:
Given that f'(x) = 8x3 – 2x
and f(2) = 8
We have to find f(x)
So, ∫f'(x)dx = ∫(8x3 – 2x)dx
f(x) = ∫(8x3 – 2x)dx
= ∫8x3dx – ∫2xdx
= (8x4)/4 – (2x2)/2 + c
= 2x4 – x2 + c
f(x) = 2x4 – x2 + c ……….(i)
As we know that f(2) = 8
So, f(2) = 2(2)4 – (2)2 + c = 8
32 – 4 + c = 8
28 + c = 8
c = -20
Now, Put c = -20 in eq(i), we get
f(x) = 2x4 – x2 – 20
Question 48. If f'(x) = asinx + bcosx and f'(0) = 4, f(0) = 3, f(π/2) = 5, find f(x)?
Solution:
Given that, f'(x) = asinx + bcosx
and f'(0) = 4, f(0) = 3, f(π/2) = 5
We have to find f(x)
So,
∫f'(x) = ∫(asinx + bcosx)dx
f(x) = -acosx + bsinx + c
f(x) = -acosx + bsinx + c ………(i)
As we know that f'(0) = 4
So, f'(0) = asin0 + bcos0 = 4
a × 0 + b × 1 = 4
b = 4
Also, f(0) = 3
f(0) = -acos0 + bsin0 + c = 3
-a + 0 + c = 3
c – a = 3 ……..(ii)
Also, f(π/2) = 5
f(π/2) = -acos(π/2) + bsin(π/2) + c = 5
-a × 0 + b × 1 + c = 5
b + c = 5
4 + c = 5 [Since, b = 4]
c = 5 – 4
c = 1
Now, put c = 1 in eq(ii), we get 1 – a = 3
-a = 3 – 1
-a = 2
a = -2
Now, put a = -2, b = 4, and c = 1 in eq(i), we get
f(x) = -(-2)cosx + 4sinx + 1
f(x) = 2cosx + 4sinx + 1
Question 49. Write the primitive or anti-derivative of f(x) = √x + 1/√x.
Solution:
We have, f(x) = √x + 1/√x
∫f(x) = ∫(√x + 1/√x)dx
= ∫x1/2dx + ∫ x-1/2 dx
= 2/3 x3/2 + 2x1/2 + c
Hence, the primitive or anti-derivative of f(x) is 2/3 x3/2 + 2x1/2 + c.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...