Class 12 RD Sharma Solutions – Chapter 19 Indefinite Integrals – Exercise 19.3 | Set 1

Question 1. Integrate ∫(2x – 3)⁵  + √3x + 2 dx

Solution:

Let I = ∫(2x – 3)⁵ + √3x + 2 dx         -(1)

On integrating the equation(1), we get

= 

= 

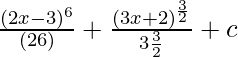
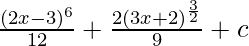
Therefore, I =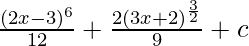 

Question 2. Integrate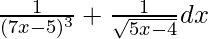 

Solution:

Let I =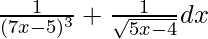

I = ∫(7x – 5)^-3 + (5x – 4)^-1/2 dx            -(1)

On integrating the equation(1), we get

= 

= 

Hence, I = 

Question 3. Integrate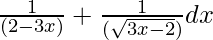 

Solution:

Let I =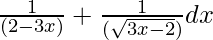 

= ∫1/(2 – 3x) + (3x – 2)^-1/2 dx            -(1)

On integrating the equation(1), we get

= log |2 – 3x| /(-3) + (2/3) × (3x – 2)^1/2 + c

= (-1/3) log|2 – 3x| + (2/3)√3x – 2 + c

Hence, I = (-1/3) log|2 – 3x| + (2/3)√3x – 2 + c

Question 4. Integrate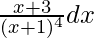 

Solution:

Let I =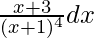 

= 

= 

= 

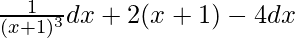
= ∫(x + 1)^-3 dx + 2∫(x + 1)^-4 dx            -(1)

On integrating the equation(1), we get

= (x + 1)^-2/(-2) + 2×(x + 1)^-3/(-3) + c

= (-1/2)(x + 1)^-2 + (-2/3)(x + 1)^-3 + c

Hence, I = (-1/2)(x + 1)^-2 + (-2/3)(x + 1)^-3 + c 

Question 5. Integrate 

Solution:

Let I = 

= 

= 

⁼ 

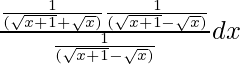
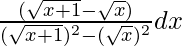
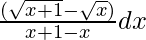
= ∫(√x + 1 – √x) dx

= ∫(x + 1)^1/2 – (x)^1/2 dx            -(1)

On integrating the equation(1), we get

= 

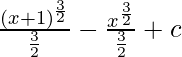
= (2/3)(x + 1)^3/2  – (2/3)(x)^3/2 + c

Hence, I = (2/3)(x + 1)^3/2 – (2/3)(x)^3/2 + c

Question 6. Integrate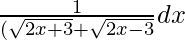 

Solution: 

Let I =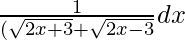 

Now multiply with the conjugate

= 

=

= 

= 

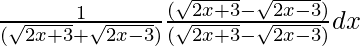
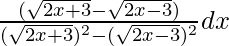
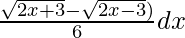
= 1/6 ∫(√2x + 3 – √2x – 3) dx

= 1/6 ∫(2x + 3)^1/2 – (2x – 3)^1/2 dx            -(1)

On integrating the equation(1), we get

= 

= 

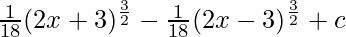
Hence, I =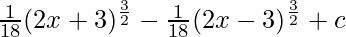 

Question 7. Integrate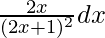 

Solution:

Let I =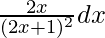 

= 

= 

=

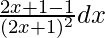
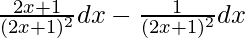
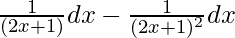
= ∫1/(2x + 1) dx – (2x + 1)^-2 dx            -(1)

On integrating the equation(1), we get

=

= (1/2) log|2x + 1| + (1/2)(2x + 1)^-1 + c

Hence, I= (1/2) log|2x + 1| + (1/2)(2x + 1)^-1 + c

Question 8. Integrate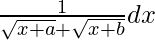 

Solution:

Let I =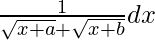 

Now multiply with the conjugate,

= 

= 

= 

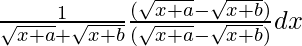
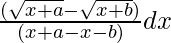
= (1/a – b)∫(x + a)^1/2 – (x + b)^1/2 dx            -(1)

On integrating the equation(1), we get

= 

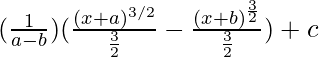
= (1/a – b) ((2/3) (x + a)^3/2 – (2/3) (x + b)^3/2) + c

Hence, I = (1/a – b) (2/3) ((x + a)^3/2 – (x + b)^3/2) + c

Question 9. Integrate ∫Sinx√1 + Cos2x dx

Solution:

Let I = ∫Sinx√1 + Cos2x dx

On  substituting the formula, we get

= ∫Sinx√(2Cos²x) dx

= ∫Sinx√2Cosx dx

= √2 ∫Sinx Cosx dx

Multiply and divide the above equation by 2

= √2/2∫2SinxCosx dx

= √2/2∫Sin2x dx            -(1)

On integrating the equation(1), we get

= √2/2 (-Cos2x/2) + c

Hence, I = (-1/2√2) Cos2x + c 

Question 10. Integrate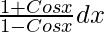 

Solution:

Let I =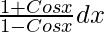 

= 

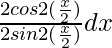
= ∫cot²(x/2) dx

= ∫cosec²(x/2) – 1 dx            -(1)

On integrating the equation(1), we get

= 

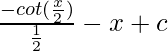
Hence, I = -2cot(x/2) – x + c