Solve the following differential equations:
Question 24. (2x – 10y3)(dy/dx) + y = 0
Solution:
We have,
(2x – 10y3)(dy/dx) + y = 0
(2x – 10y3)(dy/dx) = -y
(dx/dy) = -(2x – 10y3)/y
(dx/dy) + 2x/y = 10y2 ………..(i)
The given equation is a linear differential equation of the form
(dx/dy) + Px = Q
Where, P = 2/y, Q = 10y2
So,
I.F = e∫Pdy
= e∫(2/y)dy
= e2log|y|
= y2
The solution of a differential equation is,
x(I.F) = ∫Q(I.F)dy + c
x(y2) = ∫(10y2)(y2)dy + c
xy2 = 10(y5/5) + c
x = 2y3 + cy-2
This is the required solution.
Question 25. (x + tany)dy = sin2ydx
Solution:
We have,
(x + tany)dy = sin2ydx
(dx/dy) = (x + tany)/sin2y
(dx/dy) – cosec2y.x = tany/sin2y ………..(i)
The given equation is a linear differential equation of the form
(dx/dy) + Px = Q
Where, P = -cosec2y, Q = tany/sin2y
So, I.F = e∫Pdy
= e∫-cosec2ydy
= 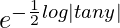
= 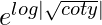
= √coty
The solution of a differential equation is,
x(I.F) = ∫Q(I.F)dy + c
x(√coty) = ∫(tany/sin2y).(√coty)dy + c
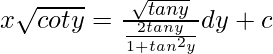
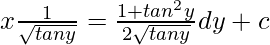
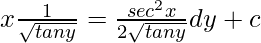
Let, tany = z
On differentiating both side we have,
sec2ydx = dz
(x/√tany) = (1/2)∫dz/√z + c
(x/√tany) = (1/2)(2√z) + c
x = (√tany)(√tany) + c(√tany)
x = tany + c(√tany)
This is the required solution.
Question 26. dx + xdy = e-ysec2ydy
Solution:
We have,
dx + xdy = e-ysec2ydy
(x – e-ysec2y)dy = -dx
(dx/dy) = (e-ysec2y-x) ………..(i)
The above equation is a linear differential equation of the form
(dx/dy) + Px = Q
Where, P = 1, Q = e-ysec2y
So, I.F = e∫Pdy
= e∫dy
= ey
The solution of a differential equation is,
x(I.F) = ∫Q(I.F)dy + c
x(ey) = ∫e-ysce2yeydy + c
x(ey) = ∫sec2ydy + c
x(ey) = tany + c
x = (tany + c)e-y
This is the required solution.
Question 27. (dy/dx) = ytanx – 2sinx
Solution:
We have,
(dy/dx) = ytanx – 2sinx
(dy/dx) – ytanx = -2sinx ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -tanx, Q = sinx
So,
I.F = e∫Pdx
= e∫-tanxdx
= e-log|secx|
= 1/secx
= cosx
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(cosx) = -2∫sinx.(cosx)dx + c
ycosx = -∫2sinx.cosxdx + c
Let, sinx = z
On differentiating both sides we have,
cosxdx = dz
ycosx = -2∫zdz + c
ycosx = -2(z2/2) + c
ycosx = -sin2xdx + c
y = secx(-sin2xdx + c)
This is the required solution.
Question 28. (dy/dx) + ycosx = sinx.cosx
Solution:
We have,
(dy/dx) + ycosx = sinx.cosx ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = cosx, Q = sinx.cosx
So,
I.F = e∫Pdx
= e∫cosxdx
= esinx
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(esinx) = ∫(esinx)(sinx.cosx)dx + c
Let, sinx = z
Differentiating both sides we get,
cosxdx = dz
y(ez) = ∫zezdz + c
y(ez) = z∫ezdz – {(dz/dz)∫ezdz}dz
y(ez) = zez – ∫ezdz + c
y(ez) = ez(z – 1) + c
y = (z – 1) + ce-z
y = (sinx – 1) + ce-sinx
This is the required solution.
Question 29. (1 + x2)(dy/dx) – 2xy = (x2 + 2)(x2 + 1)
Solution:
We have,
(1 + x2)(dy/dx) – 2xy = (x2 + 2)(x2 + 1)
(dy/dx) – 2xy/(1 + x2) = (x2 + 2) ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -2x/(1 + x2), Q = (x2 + 1)
So,
I.F = e∫Pdx
= 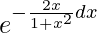
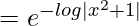
= 1/(x2+1)
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y.[1/(x2 + 1)] = ∫[(x2 + 2)/(x2 + 1)]dx + c
y/(x2 + 1) = ∫[1 + 1/(x2 + 1)]dx + c
y/(x2 + 1) = x + tan-1x + c
y = (x2 + 1)(x + tan-1x + c)
This is the required solution.
Question 30. sinx(dy/dx) + ycosx = 2sin2xcosx
Solution:
We have,
sinx(dy/dx) + ycosx = 2sin2xcosx
(dy/dx) + ycotx = 2sinx.cosx ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = cotx, Q = 2sinx.cosx
So,
I.F = e∫Pdx
= e∫cotxdx
= elog|sinx|
= sinx
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(sinx) = ∫(2sinx.cosx)sinxdx + c
Let, sinx = z
On differentiating both sides we have,
cosxdx = dz
y.z = 2∫z2 + c
y.z = (2/3)z3 + c
y.sinx = (2/3)sin3x + c
This is the required solution.
Question 31. (x2 – 1)(dy/dx) + 2(x + 2)y = 2(x + 1)
Solution:
We have,
(x2 – 1)(dy/dx) + 2(x + 2)y = 2(x + 1)
(dy/dx) + 2(x + 2)y/(x2 – 1) = 2(x + 1)/(x2 – 1)
(dy/dx) + 2(x + 2)y/(x2 – 1) = 2/(x – 1) ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = 2(x + 2)/(x2 – 1), Q = 2/(x – 1)
So,
I.F = e∫Pdx
= 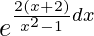
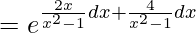
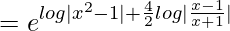
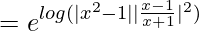
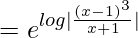
= (x – 1)3/(x + 1)
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y.[(x – 1)3/(x + 1)] = ∫[(x – 1)3/(x + 1)[{2/(x – 1)]dx + c
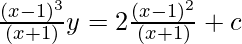
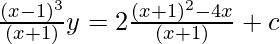
![Rendered by QuickLaTeX.com \frac{(x-1)^3}{(x+1)}y=2∫[(x+1)-4\frac{x}{(x+1)}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ae1c5c95e58db3b638e1e40f93bb40b8_l3.png)
![Rendered by QuickLaTeX.com \frac{(x-1)^3}{(x+1)}y=∫[2x+2-8\frac{x}{x+1}]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3fad92a0a254356174185ffcaa0567af_l3.png)
y.[(x – 1)3/(x + 1)] = (x2 – 6x + 8log|x + 1|) + c
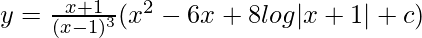
This is the required solution.
Question 32. (dy/dx) + (2y/x) = cosx
Solution:
We have,
(dy/dx) + (2y/x) = cosx ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = 2/x, Q = cosx
So,
I.F = e∫Pdx
= e∫(2/x)dx
= e2log|x|
= x2
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(x2) = ∫(x2).(cosx)dx + c
x2(y) = x2∫cosxdx – ∫{(d/dx)x2∫cosxdx}dx + c
x2y = x2sinx – 2∫xsinxdx + c
x2y = x2sinx – 2x∫sinxdx + 2∫{(dx/dx)∫sinxdx}dx + c
x2y = x2sinx + 2xcosx – 2∫cosxdx + c
x2y = x2sinx + 2xcosx – 2sinx + c
This is the required solution.
Question 33. (dy/dx) – y = xex
Solution:
We have,
(dy/dx) – y = xex ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -1, Q = xex
So,
I.F = e∫Pdx
= e∫-dx
= e-x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(e-x) = ∫(e-x)(xex)dx + c
ye-x = ∫xdx + c
ye-x = (x2/2) + c
y = [(x2/2) + c].ex
This is the required solution.
Question 34. (dy/dx) + 2y = xe4x
Solution:
We have,
(dy/dx) + 2y = xe4x ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = 2, Q = xe4x
So,
I.F = e∫Pdx
= e2∫dx
= e2x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(e2x) = ∫(e2x).(xe4x)dx + c
y(e2x) = ∫xe6xdx + c
y(e2x) = x∫e6xdx – ∫{(dx/dx)∫e6xdx}dx + c
e2xy = (xe6x)/6 – ∫(e6x/6)dx + c
e2xy = (xe6x)/6 – e6x/36 + c
y = (xe4x)/6 – e4x/36 + ce-2x
This is the required solution.
Question 35. (x + 2y2)(dy/dx) = y, given that when x = 2, y = 1
Solution:
We have,
(x + 2y2)(dy/dx) = y
(dx/dy) = (x + 2y2)/y
(dx/dy) – (x/y) = 2y ………..(i)
The given equation is a linear differential equation of the form
(dx/dy) + Px = Q
Where, P = 1/y, Q = 2y
So,
I.F = e∫Pdy
= e∫-dy/y
= e-log|y|
= 1/y
The solution of a differential equation is,
x(I.F) = ∫Q(I.F)dy + c
x(1/y) = ∫(1/y)(2y)dy + c
(x/y) = 2∫dy + c
(x/y) = 2y + c
x = 2y2 + cy
Given that when x = 2, y = 1
2 = 2 + c
c = 0
x = 2y2
This is the required solution.
Question 36(i). Find one-parameter families of solution curves of the following differential equation (dy/dx) + 3y = emx, m is a given real number
Solution:
We have,
(dy/dx) + 3y = emx ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = 3, Q = emx
So,
I.F = e∫Pdx
= e∫3dx
= e3x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(e3x) = ∫(e3x).(emx)dx + c
y(e3x) = ∫e(3+m)xdx + c
y(e3x) = e(m+3)x/(m + 3) + c
y = emx/(m + 3) + c
This is the required solution.
Question 36(ii). Find one-parameter families of solution curves of the following differential equation (dy/dx) – y = cos2x
Solution:
We have,
(dy/dx) – y = cos2x ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -1, Q = cos2x
So,
I.F = e∫Pdx
= e-∫dx
= e-x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(e-x) = ∫(e-x).(cos2x)dx + c
y(e-x) = ∫e-xcos2xdx + c
Let,
A = ∫e-xcos2xdx
= e-x∫cos2xdx – {(d/dx)e-x∫cos2xdx}dx
= (e-x/2)sin2x + ∫(e-x/2)sin2xdx
=![Rendered by QuickLaTeX.com e^{-x}sin2x+\frac{1}{2}e^{-x}∫sin2x-\frac{1}{2}∫[\frac{d}{dx}e^{-x}∫sin2xdx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7542c0c28176ea2945322dc469638396_l3.png)
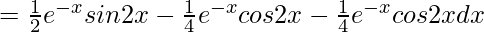
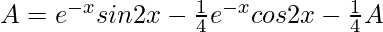
(5/4)A = (e-x/2)(2sin2x – cos2x)
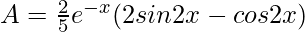
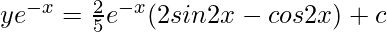
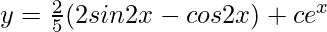
This is the required solution.
Question 36(iii). Find one-parameter families of solution curves of the following differential equation x(dy/dx) – y = (x + 1)e-x
Solution:
We have,
x(dy/dx) – y = (x + 1)e-x
(dy/dx) – y/x = [(x + 1)/x]e-x ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -1/x, Q = [(x + 1)/x]e-x
So,
I.F = e∫Pdx
= e-∫dx/x
= e-log|x|
= 1/x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(1/x) = ∫[(x+1)/x]e-x(1/x)dx + c
y/x = ∫[1/x+1/x2]e-xdx + c
Let, (1/x)e-x = z
On differentiating both sides we have
-[1/x + 1/x2]e-xdx = dz
y/x = -∫dz + c
y/x = -z + c
y/x = -(e-x/x) + c
y = -e-x + cx
This is the required solution.
Question 36(iv). Find one-parameter families of solution curves of the following differential equation x(dy/dx) + y = x4
Solution:
We have,
x(dy/dx) + y = x4
(dy/dx) + y/x = x3 ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = 1/x, Q = x3
So,
I.F = e∫Pdx
= e∫dx/x
= elog|x|
= x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(x) = ∫(x)(x3)dx + c
xy = ∫x4 + c
xy = (x5/5) + c
y = (x4/5) + c/x
This is the required solution.
Question 36(v). Find one-parameter families of solution curves of the following differential equation (xlogx)(dy/dx) + y = logx
Solution:
We have,
(xlogx)(dy/dx) + y = logx
(dy/dx) + y/xlogx = 1/x ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = 1/xlogx, Q = 1/x
So,
I.F = e∫Pdx
= e∫dx/xlogx
Let, logx = z
On differentiating both sides we have
dx/x = dz
= e∫dz/z
= elog|z|
= z
=l ogx
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(logx) = ∫(1/x)(logx)dx + c
y(logx) = ∫zdz + c (Let, logx=z and differentiating both sides)
y(logx) = (z2/2) + c
y(logx) = (logx)2/2 + c
y = logx/2 + c/logx
This is the required solution.
Question 36(vi). Find one-parameter families of solution curves of the following differential equation (dy/dx) – 2xy/(1 + x2) = x2 + 2
Solution:
We have,
(dy/dx) – 2xy/(1 + x2) = x2 + 2 ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -2x/(1 + x2), Q = x2 + 2
So,
I.F = e∫Pdx
= e-∫2xdx/(1+x2)
= e-log|1+x2|
= 1/(1+x2)
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y[1/(1 + x2)] = ∫[1/(1 + x2)](x2 + 2)dx + c
y/(1 + x2) = ∫[(x2 + 2)/(x2 + 1)]dx + c
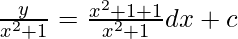
y/(1 + x2) = ∫dx + ∫dx/(x2 + 1) + c
y/(x2 + 1) = x + tan-1x + c
y = (x + tan-1x + c)(x2 + 1)
This is the required solution.
Question 36(vii). Find one-parameter families of solution curves of the following differential equation (dy/dx) + ycosx = esinxcosx
Solution:
We have,
(dy/dx) + ycosx = esinxcosx ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = cosx, Q = esinxcosx
So,
I.F = e∫Pdx
= e∫cosxdx
= esinx
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y[(esinx) = ∫(esinx)(esinxcosx)dx + c
Let, sinx = z
ON differentiating both sides we have,
cosxdx = dz
yez = ∫e2zdz + c
yez = (e2z/2) + c
y = ez/2 + ce – z
y = (esinx/2) + ce-sinx
This is the required solution.
Question 36(viii). Find one-parameter families of solution curves of the following differential equation (x + y)(dy/dx) = 1
Solution:
We have,
(x + y)(dy/dx) = 1
(dy/dx) = 1/(x + y)
(dx/dy) = (x + y)
(dx/dy) – x = y ………..(i)
The given equation is a linear differential equation of the form
(dx/dy) + Px = Q
Where, P = -1, Q = y
So,
I.F = e∫Pdy
= e-∫dy
= e-y
The solution of a differential equation is,
x(I.F) = ∫Q(I.F)dy + c
x(e-y) = ∫(e-y)(y)dy + c
xe-y = y∫e-ydy – ∫{(dy/dy)∫e-ydy}dy + c
xe-y = -ye-y + ∫e-y + c
xe-y = -ye-y – e-y + c
xe-y + ye-y + e-y = c
e-y(x + y + 1) = c
(x + y + 1) = cey
This is the required solution.
Question 36(ix). Find one-parameter families of solution curves of the following differential equation cos2x(dy/dx) = (tanx – y)
Solution:
We have,
cos2x(dy/dx) = (tanx – y)
(dy/dx) = (tanx – y)/cos2x
(dy/dx) = tanx.sec2x – ysec2x
(dy/dx) + ysec2x = tanx.sec2x ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = sec2x, Q = tanx.sec2x
So,
I.F = e∫Pdx
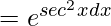
= etanx
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(etanx) = ∫(etanx)(tanx.sec2x)dx + c
Let, tanx = z
On differentiating both sides we have,
sec2xdx = dz
y(ez) = ∫zezdz + c
y(ez) = z∫ezdz – ∫{(dz/dz)∫ezdz}dz
y(ez) = zez – ∫ezdz + c
y(ez) = zez – ez + c
y = (z – 1) + c.e-z
y = (tanx – 1) + c.e-tanx
This is the required solution.
Question 36(x). Find one-parameter families of solution curves of the following differential equation e-ysec2ydy = dx + xdy
Solution:
We have,
dx + xdy = e-ysec2ydy
(x – e-ysec2y)dy = -dx
(dx/dy) = (e-ysec2y – x)
(dx/dy) + x = e-ysec2y ………..(i)
The given equation is a linear differential equation of the form
(dx/dy) + Px = Q
Where, P = 1, Q = e-ysec2y
So, I.F = e∫Pdy
= e∫dy
= ey
The solution of a differential equation is,
x(I.F) = ∫Q(I.F)dy + c
x(ey) = ∫e-ysce2yeydy + c
x(ey) = ∫sec2ydy + c
x(ey) =tany + c
x = (tan y + c)e-y
This is the required solution.
Question 36(xi). Find one-parameter families of solution curves of the following differential equation (xlogx)(dy/dx) + y = 2logx
Solution:
We have,
(xlogx)(dy/dx) + y = 2logx
(dy/dx) + y/xlogx = 2/x ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = 1/xlogx, Q = 2/x
So,
I.F = e∫Pdx
= e∫dx/xlogx
Let, logx = z
On differentiating both sides we have
dx/x = dz
= e∫dz/z
= elog|z|
= z
= logx
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(logx) = ∫(2/x)(logx)dx + c
y(logx) = 2∫zdz + c (Let, logx = z and differentiating both sides)
y(logx) = 2(z2/2) + c
y(logx) = (logx)2 + c
y = logx + c/logx
This is the required solution.
Question 36(xii). Find one-parameter families of solution curves of the following differential equation x(dy/dx) + 2y = x2logx
Solution:
We have,
x(dy/dx) + 2y = x2logx
(dy/dx) + 2y/x = xlogx ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = 2/x, Q = xlogx
So,
I.F = e∫Pdx
= e2∫dx/x
= e2logx
= x2
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(x2) = ∫(x2)(xlogx)dx + c
x2y = ∫x3logxdx + c
x2y = logx∫x3dx + ∫{(d/dx)logx∫x3dx}dx + c
x2y = (1/4)x4logx – (1/4)∫x3dx + c
x2y = (1/4)x4logx – (1/16)x4 + c
y = (x2 /16)(4logx – 1) + c/x2
This is the required solution.
Question 37. Solve the following using the initial value problem:-
(i). y’ + y = ex, y(0) = (1/2)
Solution:
We have,
y’ + y = ex
dy/dx + y = ex ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = 1, Q = ex
So, I.F = e∫Pdx
= e∫dx
= ex
The solution of differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(ex) = ∫ex.exdx + c
y(ex) = (1/2)e2x + c
At t = 0, y = (1/2)
(1/2)e0 = (1/2)e0 + c
c = 0
y(ex) = (1/2)e2x
y = (ex/2)
This is the required solution.
(ii). x(dy/dx) – y = logx, y(1) = 0
Solution:
We have,
x(dy/dx) – y = logx
(dy/dx) – y/x = logx/x ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -1/x, Q = logx/x
So,
I.F = e∫Pdx
= e-∫dx/x
= e-log|x|
= 1/x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(1/x) = ∫(1/x)(logx/x)dx + c
(y/x) = ∫(logx/x2)dx + c
(y/x) = logx∫(dx/x2) – ∫{(d/dx)logx∫(dx/x2)}dx + c
(y/x) = -(logx/x) + ∫(dx/x2) + c
(y/x) = -(logx/x) – (1/x) + c
At x = 1, y = 0
0 = -0 – 1 + c
c = 1
(y/x) = -(logx/x) – (1/x) + 1
y = x – 1 – logx
This is the required solution.
(iii). (dy/dx) + 2y = e-2xsinx, y(0) = 0
Solution:
We have,
(dy/dx) + 2y = e-2xsinx ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = 2, Q = e-2xsinx
So,
I.F = e∫Pdx
= e∫2dx
= e2x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(e2x) = ∫e-2xsinx.(e2x)dx + c
y(e2x) = ∫sinxdx + c
y(e2x) = -cosx + c
At x = 0, y = 0
0 = -1 + c
c = 1
y(e2x) = 1 – cosx
This is the required solution.
(iv). x(dy/dx) – y = (x + 1)e-x, y(1) = 0
Solution:
We have,
x(dy/dx) – y = (x + 1)e-x
(dy/dx) – (y/x) = [(x + 1)/x]e-x ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -(1/x), Q = [(x + 1)/x]e-x
So,
I.F = e∫Pdx
= e-∫(dx/x)
= e-log(x)
= elog(1/x)
= 1/x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
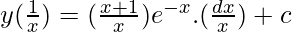
(y/x) = ∫[(1/x) + (1/x2)]e-x + c
Since, -∫[f(x) + f'(x)]e-xdx = f(x)e-x + c
(y/x) = -e-x/x + c
At x = 1, y = 0
0 = -e-1 + c
c = e-1
(y/x) = -e-x/x + e-1
y = xe-1 – e-x
This is the required solution.
(v). (1 + y2)dx + (x – 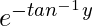 )dx = 0, y(0) = 0
)dx = 0, y(0) = 0
Solution:
We have,
(1 + y2)(dx/dy) + x = 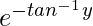
(dy/dx) + [1/(y2 + 1)]x = 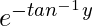 /(y2 + 1) ………..(i)
/(y2 + 1) ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Px = Q
Where, P = 1/(y2 + 1), Q = 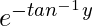 /(y2 + 1)
/(y2 + 1)
So,
I.F = e∫Pdy
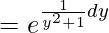
= etan-1y
The solution of a differential equation is,
x(I.F) = ∫Q(I.F)dy + c
x(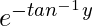 ) = ∫[
) = ∫[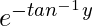 /(y2 + 1)]
/(y2 + 1)]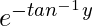 dx + c
dx + c
x(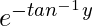 ) = ∫dy/(1 + y2) + c
) = ∫dy/(1 + y2) + c
x(etan-1y) = tan-1y + c
At x = 0, y = 0
0*e0 = 0 + c
c = 0
x(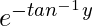 ) = tan-1y
) = tan-1y
This is the required solution.
(vi). (dy/dx) + ytanx = x2tanx + 2x, y(0) = 1
Solution:
We have,
(dy/dx) + ytanx = x2tanx + 2x ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = tanx, Q = x2tanx+2x
So,
I.F = e∫Pdx
= e∫tanxdx
= elog|secx|
= secx
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(secx) = ∫(x2tanx + 2x)secxdx + c
y(secx) = ∫(x2tanxsecx + 2xsecx)dx + c
y(secx) = ∫x2tanxsecxdx + 2∫xsecxdx + c
y(secx) = ∫x2tanxsecxdx + 2secx∫xdx – 2∫{(d/dx)secx∫xdx}dx + c
y(secx) = ∫x2tanxsecxdx + x2.secx – ∫x2tanxsecxdx + c
y(secx) = x2,(secx)+c
At, x = 0, y = 1
1 = 0 + c
c = 1
y = x2 + cosx
This is the required solution.
(vii). x(dy/dx) + y = xcosx + sinx, y(π/2) = 1
Solution:
We have,
x(dy/dx) + y = xcosx + sinx
(dy/dx) + (y/x) = cosx + sinx/x ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = 1/x, Q = cosx + sinx/x
So,
I.F = e∫Pdx
= e∫dx/x
= elog|x|
= x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(x) = ∫(cosx + sinx/x)(x)xdx + c
y(x) = ∫xcosxdx + ∫sinxdx + c
xy = x∫cosxdx – ∫{(dx/dx)∫cosxdx}dx – cosx + c
xy = xsinx – ∫sinxdx – cosx + c
xy = xsinx + cosx – cosx + c
xy = xsinx + c
At x = π/2, y = 1
π/2 = π/2sin(π/2) + c
c = 0
y = sinx
This is the required solution.
(viii). (dy/dx) + ycotx = 4xcosecx, y(π/2) = 0
Solution:
We have,
(dy/dx) + ycotx = 4xcosecx ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = cotx, Q = 4xcosecx
So,
I.F = e∫Pdx
= e∫cotx.dx
= elog|sinx|
= sinx
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(sinx) = 4∫(xcosecx)(sinx)xdx + c
y(sinx) = 4∫xdx + c
y(sinx) = 4(x2/2) + c
y(sinx) = 2x2 + c
At x = π/2, y = 0,
0 = 2(π/2)2 + c
c = -π2/2
y(sinx) = 2x2 – π2/2
This is the required solution.
(ix). (dy/dx) + 2ytanx = sinx, y = 0 when x = π/3
Solution:
We have,
(dy/dx) + 2ytanx = sinx ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = 2tanx, Q = sinx
So, I.F = e∫Pdx
= e∫2tanxdx
= e2log|secx|
= sec2x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y.sec2x = ∫sinx.sec2xdx + c
y.sec2x = ∫tanx.secxdx + c
y.sec2x = secx+c
At x = π/3, y = 0,
0 = sec2(π/3) + c
c = -2
y.sec2x = secx – 2
y = cosx – 2cos2x
This is the required solution.
(x). (dy/dx) – 3ycotx = sin2x, y = 2 when x = π/2
Solution:
We have,
(dy/dx) – 3ycotx = sin2x ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -3cotx, Q = sin2x
So, I.F = e∫Pdx
= e∫-3cotxdx
= e-3log|sinx|
= cosec3x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y.(cosec3x) = 2∫(cosec3x).(sin2x)dx + c
y.(cosec3x) = 2∫cotx.cosecxdx + c
y.(cosec3x) = -2cosesx +c
y = -2sin2x + c.sin3x
At x = π/2, y = 2.
2 = -2sin2(π/2) + c.sin3(π/2)
c = 4
y = c.sin3x – 2sin2x
This is the required solution.
(xi). (dy/dx) + ycotx = 2cosx, y(π/2) = 0
Solution:
We have,
(dy/dx) + ycotx = 2cosx ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = cotx, Q = 2cosx
So, I.F = e∫Pdx
= e∫cotxdx
= elog|sinx|
= sinx
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y.(sinx) = ∫(sinx).(2cosx)dx + c
y.(sinx) = 2∫sinx.cosxdx + c
y.(sinx) = ∫sin2xdx + c
y.(sinx) = -(cos2x/2) + c
At x = π/2, y = 0
0 = -cos(π)/2 + c
c = -(1/2)
y.(sinx) = -(cos2x/2) – (1/2)
2y(sinx) = -(1 + cos2x)
2y(sinx) = -2cos2x
y = -cotx.cosx
This is the required solution.
(xii). dy = cosx(2 – ycosecx)dx,
Solution:
We have,
dy = cosx(2 – ycosecx)dx
(dy/dx) = -ycotx + 2cosx
(dy/dx) + ycotx = 2cosx ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = cotx, Q = 2cosx
So,
I.F = e∫Pdx
= e∫cotxdx
= elog|sinx|
= sinx
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(sinx) = 2∫cosx.(sinx)dx + c
ysinx = ∫2cosx.sinxdx + c
ysinx = ∫sin2x + c
ysinx = -(cos2x/2) + c
This is the required solution.
Question 38. x(dy/dx) + 2y = x2
Solution:
We have,
x(dy/dx) + 2y = x2
(dy/dx) + 2y/x = x ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = 2/x, Q = x
So, I.F = e∫Pdx
= e2∫dx/x
= e2logx
= x2
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
yx2 = ∫x2.xdx + c
yx2 = ∫x3dx + c
x2y = (x4/4) + c
y = (x1/4) + c.x-2
This is the required solution.
Question 39. (dy/dx) – y = cosx
Solution:
We have,
(dy/dx) – y = cosx ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -1, Q = cosx
So, I.F = e∫Pdx
= e-∫dx
= e-x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(e-x) = ∫cosx.e-xdx + c
Let, I = ∫cosx.e-xdx
I = e-x∫cosxdx – ∫{(d/dx)e-x∫cosxdx}dx
I = e-xsinx + ∫e-xsinxdx
I = e-xsinx + e-x∫sinxdx-∫{(d/dx)e-x∫sinxdx}dx
I = e-xsinx – e-xcosx-∫e-xcosxdx
2I = e-x(sinx – cosx)
I = (e-x/2)(sinx – cosx)
y(e-x) = (e-x/2)(sinx – cosx) + c
y = (1/2)(sinx-cosx) + cex
This is the required solution.
Question 40. (y + 3x2)(dx/dy) = x
Solution:
We have,
(y + 3x2)(dx/dy) = x
(dy/dx) = (y + 3x2)/x
(dy/dx) – y/x = 3x ………..(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -1/x, Q = 3x
So, I.F = e∫Pdx
= e-∫dx/x
= e-logx
= 1/x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(1/x) = 3∫x.(1/x)dx + c
y(1/x) = 3∫dx + c
y/x = 3x + c
This is the required solution.
Question 41. Find a particular solution of the differential equation (dx/dy) + xcoty = y2coty + 2y, given that x = 0, when y = π/2
Solution:
We have,
(dx/dy) + xcoty = y2coty + 2y ………..(i)
The given equation is a linear differential equation of the form
(dx/dy) + Px = Q
Where, P = coty, Q = y2coty + 2y
So,
I.F = e∫Pdy
= e∫cotydy
= elog|siny|
= siny
The solution of a differential equation is,
x(I.F) = ∫Q(I.F)dy + c
x(siny) = ∫(y2coty + 2y)sinydy + c
x(siny) = ∫(y2cosy + 2xsiny)dy + c
x(siny) = y2∫cosydx – {(d/dy)y2∫cosydy}dy + ∫2ysinydy + c
x(siny) = y2siny – ∫2ysinydy + ∫2ysinydy + c
x(siny) = y2siny + c
At x = 0, y = π/2
0 = (π/2)2sin(π/2) + c
c = -π2/4
x(siny) = y2siny – π2/4
This is the required solution.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...