Class 12 RD Sharma Solutions – Chapter 19 Indefinite Integrals – Exercise 19.5
Last Updated :
07 Apr, 2021
Question 1. 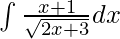
Solution:
Given integral, 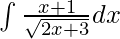
On Multiplying and dividing with 2, we get
⇒ 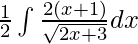
⇒ 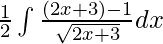
⇒ 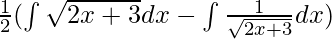
⇒ 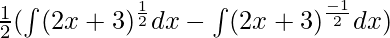
By using the formula,
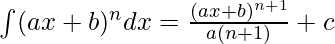 [where c is any arbitrary constant]
[where c is any arbitrary constant]
We get
⇒ ![Rendered by QuickLaTeX.com \frac{1}{2}[\frac{(2x+3)^{\frac{1}{2}+1}}{2(1/2 +1)}-\frac{(2x+3)^{\frac{-1}{2}+1}}{2(-1/2 +1)}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85862f0f019257a7a24b8a078c27edf9_l3.png)
⇒ ![Rendered by QuickLaTeX.com \frac{1}{2}[\frac{(2x+3)^{\frac{3}{2}}}{3}-\frac{(2x+3)^{\frac{1}{2}}}{1}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c4036b29b1ee76a901f2b78060af3f50_l3.png)
⇒ 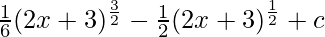
⇒ ![Rendered by QuickLaTeX.com \frac{1}{2}(2x+3)^\frac{1}{2}[\frac{2x+3}{3}-1]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-980acb97105ac29fe988b66115df4b74_l3.png)
Question 2. 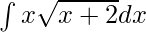
Solution:
Given integral, 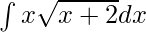
Let x + 2 =t ⇒ x = t – 2
On differentiating on both sides,
dx = dt
On substituting it in given integral, we get
⇒ 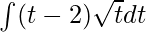
⇒ 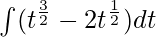
We know that, 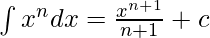 [where c is any arbitrary constant]
[where c is any arbitrary constant]
⇒ 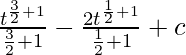
⇒ 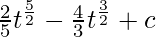
Replacing x in terms of t
⇒ 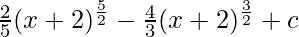
⇒ ![Rendered by QuickLaTeX.com (x+2)^\frac{3}{2}[{\frac{2(x+2)}{5}}-\frac{4}{3}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0cfe9cd2c6c4ed1177bfe89868ecb138_l3.png)
Question 3. 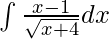
Solution:
Given integral, 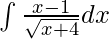
⇒ 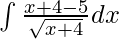
⇒ 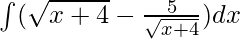
⇒ 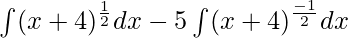
By using the formula,
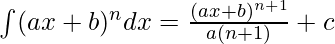 [where c is any arbitrary constant]
[where c is any arbitrary constant]
We get
⇒ 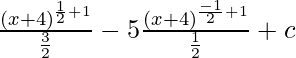
⇒ 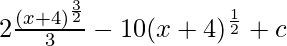
⇒ 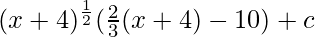
Question 4. 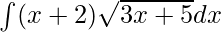
Solution:
Given integral, 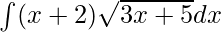
Let 3x + 5 = t
⇒ x = (t – 5)/3
On differentiating both sides,
dx = dt/3
On replacing the x terms with t,
⇒ 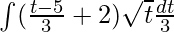
⇒ 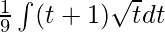
⇒ 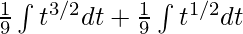
By using the formula,
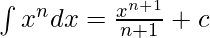 [where c is any arbitrary constant]
[where c is any arbitrary constant]
We get
⇒ 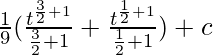
⇒ 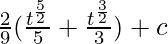
On replacing t with x terms
⇒ 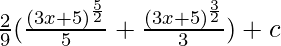
⇒ 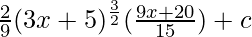
⇒ 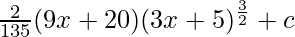
Question 5. 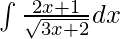
Solution:
Given integral, 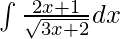
On multiplying and dividing it with 3
⇒ 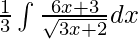
⇒ 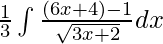
⇒ 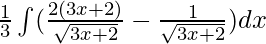
⇒ 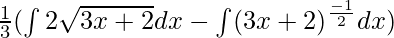
By using the formula,
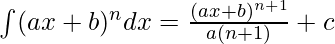 [where c is any arbitrary constant]
[where c is any arbitrary constant]
We get
⇒ ![Rendered by QuickLaTeX.com \frac{1}{3}[\frac{2(3x+2)^{\frac{3}{2}}}{\frac{9}{2}}-\frac{(3x+2)^{\frac{1}{2}}}{\frac{3}{2}}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-986596361f71e0e461f8cf97508efad1_l3.png)
⇒ ![Rendered by QuickLaTeX.com \frac{1}{3}[\frac{4}{9}{(3x+2)^\frac{3}{2}}-\frac{2}{3}(3x+2)^\frac{1}{2}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a5abac992f2642bda5d74ffff9eeffe6_l3.png)
⇒ 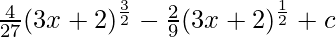
⇒ ![Rendered by QuickLaTeX.com \sqrt{3x+2}[\frac{4}{27}(3x+2)-\frac{2}{9}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ecca3c9bf6f455f66faa8881eec9db98_l3.png)
⇒ 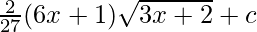
Question 6. 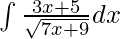
Solution:
Given integral, 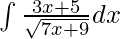
Let 7x + 9 = t
⇒ x = (t – 9)/7
On differentiating both sides,
dx = dt/7
On replacing x terms with t
⇒ 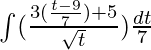
⇒ 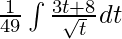
⇒ 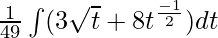
By using the formula,
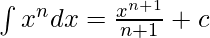 [where c is any arbitrary constant]
[where c is any arbitrary constant]
⇒ 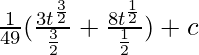
⇒ 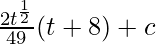
On replacing t with x terms
⇒ 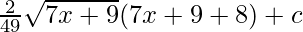
⇒ 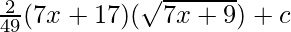
Question 7. 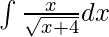
Solution:
Given integral, 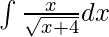
⇒ 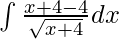
⇒ 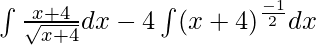
By using the formula,
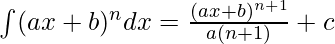 [where c is any arbitrary constant]
[where c is any arbitrary constant]
⇒ 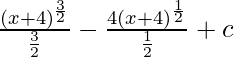
⇒ 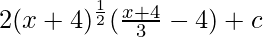
⇒ 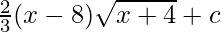
Question 8. 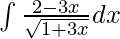
Solution:
Given integral, 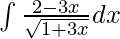
Let 1 + 3x = t
⇒ x = (t – 1)/3
On differentiating both sides, we get
dx = dt/3
On replacing x with t
⇒ 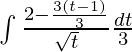
⇒ 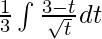
⇒ 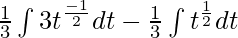
By using the formula,
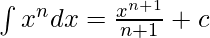 [where c is any arbitrary constant]
[where c is any arbitrary constant]
⇒ ![Rendered by QuickLaTeX.com \frac{1}{3}[\frac{3t^\frac{1}{2}}{\frac{1}{2}}]-\frac{1}{3}[\frac{t^\frac{3}{2}}{\frac{3}{2}}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4b4e3dfcdd30b7aa9137810470c85f90_l3.png)
Now on replacing t in terms of x
⇒ 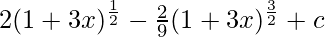
⇒ ![Rendered by QuickLaTeX.com 2(1+3x)^{\frac{1}{2}}[1-\frac{1+3x}{9}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3ec470a47f0eeba58c496f10b0f9a4dd_l3.png)
⇒ 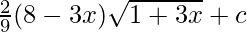
Question 9. 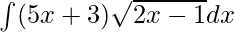
Solution:
Given integral, 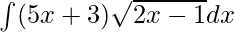
Let 2x – 1 = t2
⇒ x = (t2 + 1)/2
On differentiating on both sides,
dx = tdt
⇒ 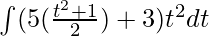
⇒ 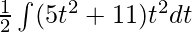
⇒ 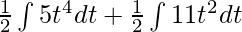
By using the formula,
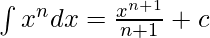 [where c is any arbitrary constant]
[where c is any arbitrary constant]
⇒ ![Rendered by QuickLaTeX.com \frac{1}{2}{[\frac{5t^5}{5}]}+\frac{1}{2}{[\frac{11t^3}{3}]}+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-549b1aacbf45087bf45f6caf4302a43b_l3.png)
On replacing t with x terms
⇒ ![Rendered by QuickLaTeX.com \frac{1}{2}[(2x-1)^{\frac{5}{2}}+\frac{11}{3}(2x-1)^{\frac{3}{2}}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9db8609f4eb2e18e19cc61e6d1a0f846_l3.png)
⇒ ![Rendered by QuickLaTeX.com \frac{(2x-1)^{\frac{3}{2}}}{2}[2x-1+{\frac{11}{3}}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-87b7fd315797b5b5b514d59a6fb7ad36_l3.png)
⇒ 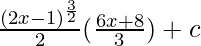
⇒ 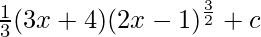
Question 10. 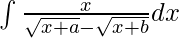
Solution:
Given integral, 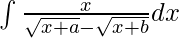
On multiplying and dividing the given integral with 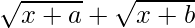
We know that (a + b)(a – b) = a2 – b2
⇒ 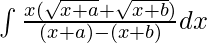
⇒ 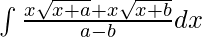
⇒ ![Rendered by QuickLaTeX.com \frac{1}{a-b}[\int x\sqrt{x+a} dx+\int x\sqrt{x+b}dx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1919af7829b6eaf68a2592336bb6ccbc_l3.png)
⇒ 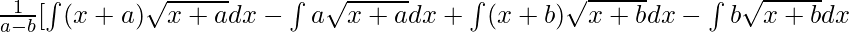
By using the formula,
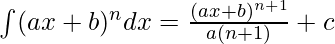 [where c is any arbitrary constant]
[where c is any arbitrary constant]
⇒ ![Rendered by QuickLaTeX.com \frac{1}{a-b}[\frac{(x+a)^\frac{5}{2}}{\frac{5}{2}}-{\frac{a(x+a)^{\frac{3}{2}}}{\frac{3}{2}}}+\frac{(x+b)^\frac{5}{2}}{\frac{5}{2}}-{\frac{b(x+b)^{\frac{3}{2}}}{\frac{3}{2}}}]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9eecb61d1d46eea2fb8e3e6c4477408e_l3.png)
⇒ ![Rendered by QuickLaTeX.com \frac{2}{a-b}[\frac{(x+a)^\frac{5}{2}+(x+b)^\frac{5}{2}}{5}-(\frac{a(x+a)^\frac{3}{2}+b(x+b)^\frac{3}{2}}{3})]+c](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8e5c69d58d278c1af81116f6df38ec79_l3.png)
Share your thoughts in the comments
Please Login to comment...