Evaluate the following integrals:
Question 1. ∫x cosxdx
Solution:
Given that, I = ∫x cosxdx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = x∫cosxdx – ∫(1 × ∫cosxdx)dx + c
= xsinx – ∫sinxdx + c
Hence, I = x sinx + cosx + c
Question 2. ∫log(x + 1)dx
Solution:
Given that, I = ∫log(x + 1)dx
= ∫1 × log(x + 1)dx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = log(x + 1)∫1dx – ∫(1/(x + 1) × ∫ 1dx)dx + c
= xlog(x + 1) – ∫(x/(x + 1))dx + c
= x log(x + 1) – ∫(1 – 1/(x + 1))dx + c
Hence, I = x log(x + 1) – x + log(x + 1) + c
Question 3. ∫x3 logxdx
Solution:
Given that, I = ∫ x3 logxdx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = logx ∫x3 dx – ∫(1/x × ∫x3 dx)dx + c
= x4/4 logx – ∫x4/4x dx+c
= x4/4 logx – 1/4∫x3 dx + c
= x4/4 logx – 1/4 ∫x4/4 dx + c
I = x4/4 logx – 1/16 x4 + c
Question 4. ∫xex dx
Solution:
Given that I = ∫xex dx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = xex – ∫1.ex dx
= xex – ex + c
Hence, I = = xex – ex + c
Question 5. ∫xe2x dx
Solution:
Given that, I = ∫xe2x dx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = x∫e2x dx – ∫(1 × ∫ e2x dx) dx + c
= x∫e2x dx – ∫(1 × ∫e2x dx)dx + c
= (xe2x)/2 – ∫(e2x/2)dx + c
= (xe2x)/2 – e2x/4 + c
Hence, I = (x/2 – 1/4) e2x + c
Question 6. ∫x2 e-x dx
Solution:
Given that I = ∫x2 e-x dx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = x2 ∫e-x dx – ∫(2x∫e-x dx)dx
= -x2 e-x – ∫(2x)(-e-x)dx
= -x2 e-x + 2∫xe-x dx
= -x2 e-x + 2[x∫e-x dx – ∫(1 × ∫ e-x dx) dx]
= -x2 e-x + 2[x(-e-x) – ∫(-e-x)dx]
= -x2 e-x – 2xe-x + 2∫e-x dx
Hence, I = -x2 e-x – 2xe-x – 2e-x + c
Question 7. ∫ x2cosxdx
Solution:
Given that, I = ∫ x2cosxdx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = x2 ∫ cosxdx – ∫(2x)cosxdx)dx
= x2 sinx – 2∫(x)(sinx)dx
= x2 sinx – 2[x∫sinxdx – ∫(1 × ∫sinxdx)dx]
= x2 sinx – 2[x(-cosx) – ∫(-cosx)dx]
= x2 sinx + 2xcosx – 2∫(cosx)dx
Hence, I = x2sinx + 2xcosx – 2sinx + c
Question 8. ∫x2cos2xdx
Solution:
Given that, I = ∫x2cos2xdx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = x2 ∫cos2xdx – ∫(2x∫ cos2xdx)dx
= x2 (sin2x)/2 – 2∫x((sin2x)/2)dx
= 1/2 x2 sin2x – ∫xsin2xdx
= 1/2 x2 sin2x – [x∫sin2xdx – ∫ (1∫ sin2xdx)dx]
= 1/2 x2 sin2x – [x((-cos2x)/2) – ∫(-(cos2x)/2)dx]
= 1/2 x2sin2x + x/2 cos2x – 1/2 ∫(cos2x)dx
Hence, I = 1/2 x2 sin2x + x/2 cos2x – 1/4 sin2x + c
Question 9. ∫xsin2xdx
Solution:
Given that, I =∫xsin2xdx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = x∫sin2xdx – ∫(1)sin2xdx)dx
= x(-(cos2x)/2) – ∫(-(cos2x)/2)dx
= -x/2 cos2x + 1/2 ∫cos2xdx
= -x/2 cos2x + 1/2(sin2x)/2 + c
Hence, I = -x/2 cos2x + 1/4 sin2x + c
Question 10. ∫(log(logx))/x dx
Solution:
Given that, I = ∫(log(logx))/x dx
= ∫(1/x)(log(logx))dx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = loglogx]1/x dx – ∫(1/(xlogx)∫1/x dx)dx
= logx × log(logx) – ∫(1/(xlogx) logx)dx
= logx × log(logx) – ∫1/x dx
= logx × log(logx) – logx + c
Hence, I = logx(loglogx – 1) + c
Question 11. ∫x2 cosxdx
Solution:
Given that I = ∫x2 cosxdx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = x2∫ cosxdx – ∫(2x]cosxdx)dx
= x2sinx – 2∫xsinxdx
= x2 sinx – 2[x∫sinxdx – ∫(1]sinxdx)dx]
= x2 sinx – 2[x(-cosx) – ∫(-cosx)dx]
= x2 sinx + 2xcosx – 2∫(cosx)dx
Hence, I = x2 sinx + 2xcosx – 2sinx + c
Question 12. ∫xcosec2xdx
Solution :
Given that, I = ∫xcosec2xdx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = x∫cosec2xdx – ∫(∫ cosec2xdx)dx
= -xcotx + ∫cotxdx
= -x cotx + log |sinx| + c
Hence, I = -x cotx + log |sinx| + c
Question 13. ∫xcos2xdx
Solution:
Given that, I = ∫xcos2xdx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = x∫cos2xdx – ∫(1∫ cos2xdx)dx
= x∫((cos2x + 1)/2)dx – ∫(∫((1 + cos2x)/2)dx)dx
= x/2 [(sin2x)/2 + x] – 1/2∫(x + (sin2x)/2)dx
= x/4 sin2x + x2/2 – 1/2 × x2/2 – 1/4 (-(cos2x)/2) + c
Hence, I = x/4 sin2x + x2/4 + 1/8 cos2x + c
Question 14. ∫xn logx dx
Solution:
Given that, I = ∫xn logxdx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = logx∫xn dx – ∫(1/x ∫xndx)dx
= xn+1/(n + 1) logx – ∫(1/x × xn+1/(n + 1))dx
= xn+1/(n + 1) logx – ∫(xn/(n + 1))dx
Hence, I = xn+1/(n + 1) logx – 1/(n + 1)2 × (xn+1) + c
Question 15. ∫(logx)/xn dx
Solution:
Given that, I = ∫(logx)/xn dx = ∫(logx)(1/xn)dx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
I = logx∫(1/xn)dx – ∫((d(logx))/dx)(∫(1/xn)dx)dx
= logx(x1-n/(1 – n)) – ∫1/x (x1-n/(1 – n))dx
= logx(x1-n/(1 – n)) – ∫(xn/(1 – n))dx
= logx(x1-n/(1 – n)) – (1/(1 – n))(x1-n/(1 – n))
Hence, I = logx(x1-n/(1 – n)) – (x1-n/([1 – n]2)) + c
Question 16. ∫x2 sin2xdx
Solution:
Given that, I = ∫x2 sin2xdx
= ∫x2 ((1 – cos2x)/2)dx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
= ∫x2/2 dx – ∫((x2 cos2x)/2)dx
= x3/6 – 1/2 [∫x2 cos2xdx]
= x3/6 – 1/2 [x2 ∫cos2xdx – ∫ (2x∫cos2xdx)dx]
= x3/6 – 1/2 (x2(sin2x)/2) + 1/2 × 2∫(x (sin2x)/2)dx
= x3/6 – 1/4 x2sin2x + 1/2 [x ∫sin2xdx – ∫(1∫sin2xdx)dx]
= x3/6 – 1/4 x2 sin2x + 1/2 [x(-(cos2x)/2) – ∫(-(cos2x)/2)dx]
= x3/6 – 1/4 x2 sin2x + 1/2 x(-(cos2x)/2) + 1/4 × (sin2x/2) + c
= x3/6 – 1/4 x2 sin2x – 1/4 x(cos2x) + 1/8 × (sin2x) + c
Hence, I = x3/6 – 1/4 x2 sin2x – 1/4 x(cos2x) + 1/8 × (sin2x) + c
Question 17. 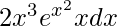
Solution:
Given that, l = 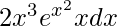
Let us assume, x2 = t
2xdx = dt
I = ∫t × et dt
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
= t∫et dt – ∫(1 × ∫etdt)dt
= tet – ∫et dt
= tet – et + c
= et-1 + c
Hence, I = 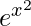 (x2 – 1) + c
(x2 – 1) + c
Question 18. ∫x3 cosx2 dx
Solution:
Given that, I = ∫x3 cosx2 dx
Let us assume x2 = t
2xdx = dt
I = 1/2 ∫tcostdt
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
= 1/2[t∫costdt – ∫(1 × ∫costdt)dt]
= 1/2 [t × sint – ∫sintdt]
= 1/2[tsint + cost] + c
Hence, I = 1/2 [x² sinx2 + cosx2] + c
Question 19. ∫xsinxcosxdx
Solution:
Given that, I = ∫xsinxcosxdx
= ∫x/2(2sinxcosx)dx
= 1/2 ∫xsin2xdx
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
= 1/2 [x∫sin2xdx – ∫(1 × ∫sin2xdx)dx]
= 1/2 [x((-cos2x)/2) – ∫((-cos2x)/2)dx]
= -1/4 xcos2x + 1/4 ∫cos2xdx
Hence, I = -1/4 xcos2x + 1/8 sin2x + c
Question 20. ∫sinx(logcosx)dx
Solution:
Given that, I = ∫sinx(logcosx)dx
Let us considered, cosx = t
-sinxdx = dt
I = -∫ logtdt
= -∫1 × logtdt
Using integration by parts,
∫u v dx = v∫ u dx – ∫{d/dx(v) × ∫u dx}dx + c
We get
= -[logt∫dt – ∫(1/t × ∫dt)dt]
= -[tlogt – ∫1/t × tdt]
= -[tlogt-∫ dt]
= -[tlogt – t + c1 ]
= t(1 – logt) + c
Hence, I = cosx(1 – logcosx) + c
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...