Class 12 RD Sharma Solutions – Chapter 11 Differentiation – Exercise 11.2 | Set 2
Last Updated :
14 Jul, 2021
Question 25. Differentiate y = 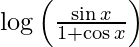 with respect to x.
with respect to x.
Solution:
We have,
y = 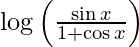
On differentiating y with respect to x we get,

On using chain rule, we have
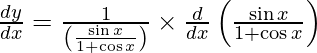
On using quotient rule, we have
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left( \frac{1 + \cos x}{\sin x} \right)\left[ \frac{\left( 1 + \cos x \right)\frac{d}{dx}\left( \sin x \right) - \sin x\frac{d}{dx}\left( 1 + \cos x \right)}{\left( 1 + \cos x \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ec6979088679ed736deaa02e85295ce4_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left( \frac{1 + \cos x}{\sin x} \right)\left[ \frac{\left( 1 + \cos x \right)\left( \cos x \right) - \sin x\left( - \sin x \right)}{\left( 1 + \cos x \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2e9acff8b47c9ce393ca3c5b76e28bf3_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left( \frac{1 + \cos x}{\sin x} \right)\left[ \frac{\cos x + \cos^2 x + \sin^2 x}{\left( 1 + \cos x \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-06b610623c0b48085967bf61c4756572_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left( \frac{1 + \cos x}{\sin x} \right)\left[ \frac{\left( 1 + \cos x \right)}{\left( 1 + \cos x \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dd9878a915a7a31343fbaaa35a5d61f1_l3.png)
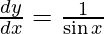
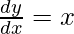
Question 26. Differentiate y = 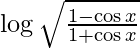 with respect to x.
with respect to x.
Solution:
We have,
y = 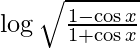
y = 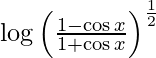
As 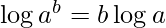 , we get
, we get
y = 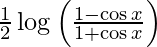
On differentiating y with respect to x we get,

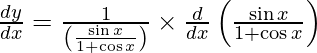
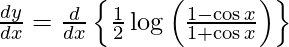
On using chain rule, we have

On using quotient rule, we have
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{2}\left( \frac{1 + \cos x}{1 - \cos x} \right)\left[ \frac{\left( 1 + \cos x \right)\frac{d}{dx}\left( 1 - \cos x \right) - \left( 1 - \cos x \right)\frac{d}{dx}\left( 1 + \cos x \right)}{\left( 1 + cos x \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc367ae7b9c5b5979e5c3d24c9d9b57b_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{2}\left( \frac{1 + \cos x}{1 - \cos x} \right)\left[ \frac{\left( 1 + \cos x \right)\left( \sin x \right) - \left( 1 - \cos x \right)\left( - \sin x \right)}{\left( 1 + \cos x \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-978a2d66aa4e0e1413219f73d0cae814_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{2}\left( \frac{1 + \cos x}{1 - \cos x} \right)\left[ \frac{\sin x + \sin x \cos x + \sin x - \sin x \cos x}{\left( 1 + \cos x \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d7db66c9fa7428f3d971f6a90db3874_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{2}\left( \frac{1 + \cos x}{1 - \cos x} \right)\left[ \frac{2\sin x}{\left( 1 + \cos x \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-34f0f81bbd70416bf39d0360a5f636b3_l3.png)
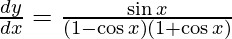
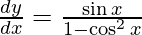
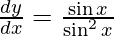
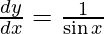
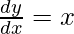
Question 27. Differentiate y =  with respect to x.
with respect to x.
Solution:
We have,
y = 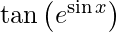
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left[ \tan\left( e^{\sin x} \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d41c9a3a3ea32f68d09ba870544d51f_l3.png)
On using chain rule, we have
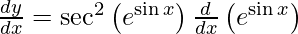
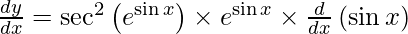
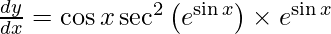
Question 28. Differentiate y = 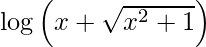 with respect to x.
with respect to x.
Solution:
We have,
I = 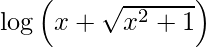
On differentiating y with respect to x we get,
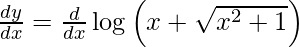
On using chain rule, we have
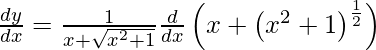
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{x + \sqrt{x^2 + 1}}\left[ 1 + \frac{1}{2} \left( x^2 + 1 \right)^{\frac{1}{2} - 1} \frac{d}{dx}\left( x^2 + 1 \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8d3f1bd3cbeff36ce0faa924086d3c85_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{x + \sqrt{x^2 + 1}}\left[ 1 + \frac{1}{2\sqrt{x^2 + 1}} \times 2x \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-91e9b620630cb0ac5f745bb12bd25301_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{x + \sqrt{x^2 + 1}}\left[ \frac{\sqrt{x^2 + 1} + x}{\sqrt{x^2 + 1}} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-36d1c2775201fe2fdf668ae57255b90d_l3.png)
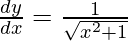
Question 29. Differentiate y = 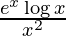 with respect to x.
with respect to x.
Solution:
We have,
y = 
On differentiating y with respect to x we get,
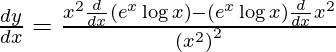
On using quotient rule, we have
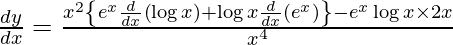
On using product rule, we have
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{x^2 \left[ \frac{e^x}{x} + e^x \log x \right] - 2x e^x \log x}{x^4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-04a3dba17ee4d0d6cf0616f692ee9264_l3.png)
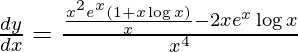
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{x e^x \left[ 1 + x\log x - 2\log x \right]}{x^4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a057db7949dda10e7418b83a0d8fc258_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{x e^x}{x^3}\left[ \frac{1}{x} + \frac{x \log x}{x} - \frac{2\log x}{x} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54a8265feaec216345bf7e2692f02f48_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = e^x x^{- 2} \left[ \frac{1}{x} + \log x - \frac{2}{x}\log x \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-842208928049a31a69fdf4edd679ce74_l3.png)
Question 30. Differentiate y = 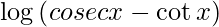 with respect to x.
with respect to x.
Solution:
We have,
y = 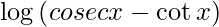
On differentiating y with respect to x we get,
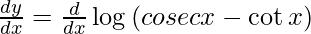
On using chain rule, we have
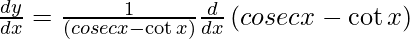
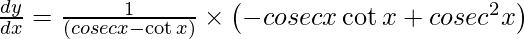
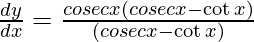
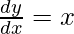
Question 31. Differentiate y = 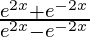 with respect to x.
with respect to x.
Solution:
We have,
y = 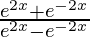
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left[ \frac{e^{2x} + e^{- 2x}}{e^{2x} - e^{- 2x}} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ef6d40cf846b20f5e69c4cc92a17b4cf_l3.png)
On using quotient rule and chain rule, we get
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{\left( e^{2x} - e^{- 2x} \right)\frac{d}{dx}\left( e^{2x} + e^{- 2x} \right) - \left( e^{2x} + e^{- 2x} \right)\frac{d}{dx}\left( e^{2x} - e^{- 2x} \right)}{\left( e^{2x} - e^{- 2x} \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b788ef6dc074b6509577e40b6933695f_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{\left( e^{2x} - e^{- 2x} \right)\left[ e^{2x} \frac{d}{dx}\left( 2x \right) + e^{- 2x} \frac{d}{dx}\left( - 2x \right) \right] - \left( e^{2x} + e^{- 2x} \right)\left[ e^{2x} \frac{d}{dx}\left( 2x \right) - e^{- 2x} \frac{d}{dx}\left( - 2x \right) \right]}{\left( e^{2x} - e^{- 2x} \right)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-75544dfd4f8b3bb0365caf1ce750f557_l3.png)
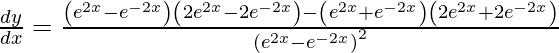
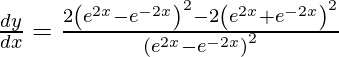
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{2\left[ e^{4x} + e^{- 4x} - 2 e^{2x} e^{- 2x} - e^{4x} - e^{- 4x} - 2 e^{2x} e^{- 2x} \right]}{\left( e^{2x} - e^{- 2x} \right)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b9cbb62c5b9fd65e187a87f4b0da86bb_l3.png)
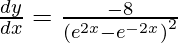
Question 32. Differentiate y =  with respect to x.
with respect to x.
Solution:
We have,
y = 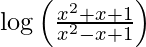
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left[ \log\left( \frac{x^2 + x + 1}{x^2 - x + 1} \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-91c9075bd6044d9f632240e17fc8047f_l3.png)
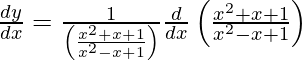
On using quotient rule and chain rule, we get
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left( \frac{x^2 - x + 1}{x^2 + x + 1} \right)\left[ \frac{\left( x^2 - x + 1 \right)\frac{d}{dx}\left( x^2 + x + 1 \right) - \left( x^2 + x + 1 \right)\frac{d}{dx}\left( x^2 - x + 1 \right)}{\left( x^2 - x + 1 \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-42201630d1af800959e723487f28d48a_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left( \frac{x^2 - x + 1}{x^2 + x + 1} \right)\left[ \frac{\left( x^2 - x + 1 \right)\left( 2x + 1 \right) - \left( x^2 + x + 1 \right)\left( 2x - 1 \right)}{\left( x^2 - x + 1 \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9e4aaf30a10892a588c231dea2b77c5c_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left( \frac{x^2 - x + 1}{x^2 + x + 1} \right)\left[ \frac{2 x^3 - 2 x^2 + 2x + x^2 - x + 1 - 2 x^3 - 2 x^2 - 2x + x^2 + x + 1}{\left( x^2 - x + 1 \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3d4f150e0f2ddb40f0fa24f6f7ad2d73_l3.png)

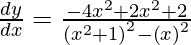
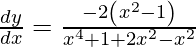
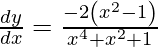
Question 33. Differentiate y =  with respect to x.
with respect to x.
Solution:
We have,
y = 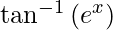
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left[ \tan^{- 1} \left( e^x \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b8713bc70408b57ec7f4638f869753e5_l3.png)
On using chain rule, we have
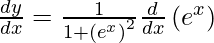
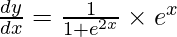
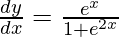
Question 34. Differentiate y = 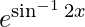 with respect to x.
with respect to x.
Solution:
We have,
y = 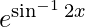
On differentiating y with respect to x we get,

On using chain rule, we have
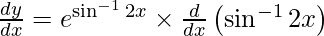
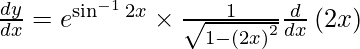
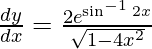
Question 35. Differentiate y = 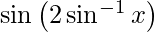 with respect to x.
with respect to x.
Solution:
We have,
y = 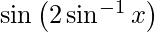
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left[ \sin\left( 2 \sin^{- 1} x \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1b399f949d044364a6f73e65e92fdbde_l3.png)
On using chain rule, we have

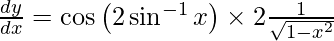
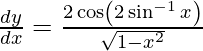
Question 36. Differentiate y = 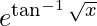 with respect to x.
with respect to x.
Solution:
We have,
y = 
On differentiating y with respect to x we get,
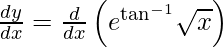
On using chain rule, we have
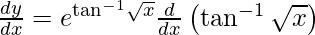
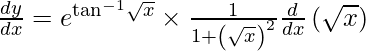
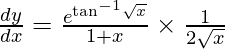
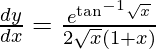
Question 37. Differentiate y = 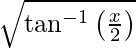 with respect to x.
with respect to x.
Solution:
We have,
y = 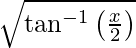
y = 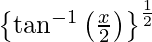
On differentiating y with respect to x we get,
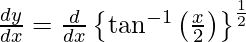
On using chain rule, we have
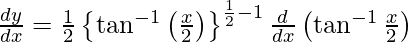
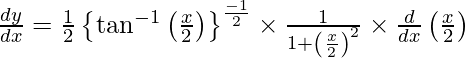
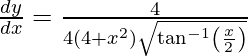

Question 38. Differentiate y = 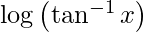 with respect to x.
with respect to x.
Solution:
We have,
y = 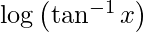
On differentiating y with respect to x we get,
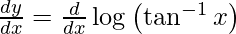
On using chain rule, we have
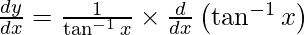
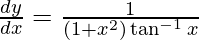
Question 39. Differentiate y = 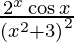 with respect to x.
with respect to x.
Solution:
We have,
y = 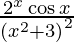
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left[ \frac{2^x \cos x}{\left( x^2 + 3 \right)^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8e00d262b696184b4fce1caa677014be_l3.png)
On using quotient rule, we have
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{\left( x^2 + 3 \right)^2 \frac{d}{dx}\left( 2^x \cos x \right) - \left( 2^x \cos x \right)\frac{d}{dx} \left( x^2 + 3 \right)^2}{\left[ \left( x^2 + 3 \right)^2 \right]^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b3fb9d4bdc5515923eabd3c26da5d7c6_l3.png)
On using product rule and chain rule, we have
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{\left( x^2 + 3 \right)^2 \left\{ 2^x \frac{d}{dx}\cos x + \cos x\frac{d}{dx} 2^x \right\} - \left( 2^x \cos x \right)2\left( x^2 + 3 \right)\frac{d}{dx}\left( x^2 + 3 \right)}{\left( x^2 + 3 \right)^4} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-20883b71fc836a88f58b055ec377d5da_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{\left( x^2 + 3 \right)^2 \left\{ - 2^x \sin x + \cos x 2^x \log_e 2 \right\} - 2\left( 2^x \cos x \right)\left( x^2 + 3 \right)\left( 2x \right)}{\left( x^2 + 3 \right)^4} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1b5f61c2605365325dbbd1e01e7b4419_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{2^x \left( x^2 + 3 \right)\left\{ \left( x^2 + 3 \right)\left( \cos x \log_e 2 - \sin x \right) - 4x \cos x \right\}}{\left( x^2 + 3 \right)^4} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-417bcbce7f35a677a4ac87f96c4a3b1a_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{2^x}{\left( x^2 + 3 \right)^2}\left[ \cos x \log_e 2 - \sin x - \frac{4x \cos x}{\left( x^2 + 3 \right)} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-74b9de041bce9ef6150ee20569fbc0f9_l3.png)
Question 40. Differentiate y = 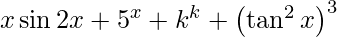 with respect to x.
with respect to x.
Solution:
We have,
y = 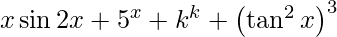
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left[ x \sin2x + 5^x + k^k + \left( \tan^6 x \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c33a9e15be459e1cd2902d71f2c44cce_l3.png)
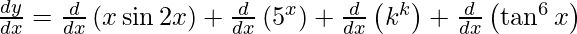
On using product rule and chain rule, we have
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ x\frac{d}{dx}\left( \sin2x \right) + \sin2x\frac{d}{dx}\left( x \right) \right] + 5^x \log_e 5 + 0 + 6 \tan^5 x \times \frac{d}{dx}\left( \tan x \right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e7b376f6807023e898bd117b8f49d792_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ x \cos2x\frac{d}{dx}\left( 2x \right) + \sin2x \right] + 5^x \log_e 5 + 6 \tan^5 x \sec^2 x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f75a13ab76ccb9a6e9fd19a17e0a3e9d_l3.png)
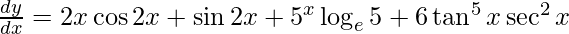
Question 41. Differentiate y = 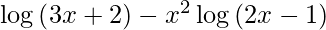 with respect to x.
with respect to x.
Solution:
We have,
y = 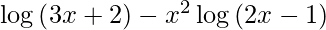
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left[ \log\left( 3x + 2 \right) - x^2 \log\left( 2x - 1 \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8a053098d385cb26530e5a4f60ad88e8_l3.png)
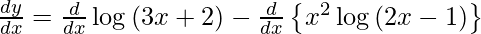
On using product rule and chain rule, we have
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{\left( 3x + 2 \right)}\frac{d}{dx}\left( 3x + 2 \right) - \left[ x^2 \frac{d}{dx}\log\left( 2x - 1 \right) + \log\left( 2x - 1 \right)\frac{d}{dx}\left( x^2 \right) \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5f90d46bd21e4f23ba348a4b8220a3ae_l3.png)
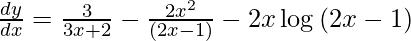
Question 42. Differentiate y = 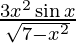 with respect to x.
with respect to x.
Solution:
We have,
y = 
On differentiating y with respect to x we get,
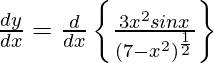
On using quotient rule, chain rule and product rule we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{\left( 7 - x^2 \right)^\frac{1}{2} \times \frac{d}{dx}\left( 3 x^2 \sin x \right) - \left( 3 x^2 \sin x \right)\frac{d}{dx} \left( 7 - x^2 \right)^\frac{1}{2}}{\left[ \left( 7 - x^2 \right)^\frac{1}{2} \right]^2} \left[ \text{} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e9acd57eb124c8006c5a6ce9fd11dfde_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{\left( 7 - x^2 \right)^\frac{1}{2} \times 3\left[ x^2 \frac{d}{dx}\left( \sin x \right) + \sin x\frac{d}{dx}\left( x^2 \right) \right] - 3 x^2 \sin x \times \frac{1}{2}\left( 7 - x^2 \right) \times \frac{d}{dx}\left( 7 - x^2 \right)}{\left( 7 - x^2 \right)} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-860d89eed6fb0b7169a89f3045baefae_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{\left( 7 - x^2 \right)^\frac{1}{2} 3\left( x^2 \cos x + 2x \sin x \right) - 3 x^2 \sin x \times \frac{1}{2} \left( 7 - x^2 \right)^\frac{- 1}{2} \left( - 2x \right)}{\left( 7 - x^2 \right)} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bbb92e4d0850ca9e82839b29926a1c58_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{\left( 7 - x^2 \right)^\frac{1}{2} \times 3\left( x^2 \cos x + 2x \sin x \right)}{\left( 7 - x^2 \right)} + \frac{3 x^3 \sin x \left( 7 - x^2 \right)^\frac{- 1}{2}}{\left( 7 - x^2 \right)} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f03028fe93c929affdf3f8c409250f9d_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \left[ \frac{6x \sin x + 3 x^2 \cos x}{\sqrt{\left( 7 - x^2 \right)}} + \frac{3 x^3 \sin x}{\left( 7 - x^2 \right)^\frac{3}{2}} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2dc93dbba944dedbb730be72400bcc46_l3.png)
Question 43. Differentiate y = 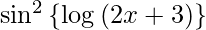 with respect to x.
with respect to x.
Solution:
We have,
y = 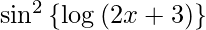
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left[ \sin^2 \left\{ \log\left( 2x + 3 \right) \right\} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4b6599ec06fb15cffa932c07cc880fcb_l3.png)
On using chain rule, we get

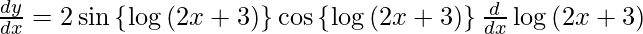
As 2 sin A cos A = sin 2A, we get
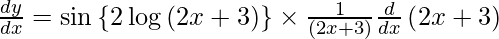
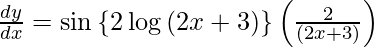
Question 44. Differentiate y = 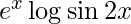 with respect to x.
with respect to x.
Solution:
We have,
y = 
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{d}{dx}\left[ e^x \log \sin2x \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c303443d5efaf4c4dfe0df2b45718caf_l3.png)
On using product rule and chain rule, we have
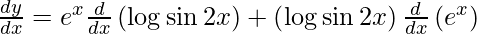
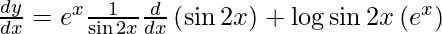
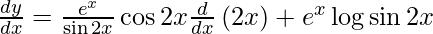

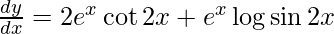
Question 45. Differentiate y = 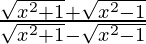 with respect to x.
with respect to x.
Solution:
We have,
y = 
On rationalizing we get,
y = 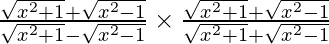
y = 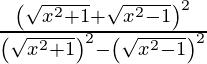
y = 
y = 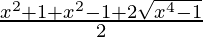
y = 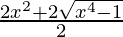
y = 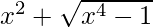
On differentiating y with respect to x we get,

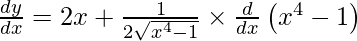
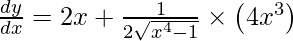

Question 46. Differentiate y = ![Rendered by QuickLaTeX.com \log [x+2+\sqrt{x^2+4x+1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2ddaff463fadd6a2cf46ec6f54f00673_l3.png) with respect to x.
with respect to x.
Solution:
We have,
y = ![Rendered by QuickLaTeX.com \log [x+2+\sqrt{x^2+4x+1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8bb98c82f918343793220dc2f96f9e90_l3.png)
On differentiating y with respect to x we get,
![Rendered by QuickLaTeX.com \frac{d y}{d x}=\frac{d}{dx}\log[x+2+\sqrt{x^2+4x+1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-52f41014d889765d4e2d85e69cbaaf0a_l3.png)
On using chain rule, we have
![Rendered by QuickLaTeX.com \frac{d y}{d x}=\frac{1}{([x+2+sqrt(x^4+4x+1)])}\frac{d}{dx}[x+2+(x^2+4x+1)^{\frac{1}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-132ff2412d4c2897e3f203839de8a579_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x}=\frac{1}{x+2+sqrt(x^4+4x+1)}[1+0+\frac{1}{2}(x^2+4x+1)^{-1/2}\frac{d}{dx}(x^2+4x+1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-abadf279d21f9719b54e9ea381d5f0b2_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x}=\frac{1+\frac{2x+4}{2\sqrt{x^2+4x+1}}}{[x+2+\sqrt{x^4+4x+1}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e742a65559aed941e1550eaca219408a_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x}=\frac{\sqrt{x^4+4x+1}+x+2}{[x+2+\sqrt{x^4+4x+1}]\sqrt{x^4+4x+1}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-857b153916fc66d5fee2fc8abb5dcdd7_l3.png)
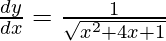
Question 47. Differentiate y = 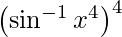 with respect to x.
with respect to x.
Solution:
We have,
y = 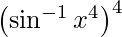
On differentiating y with respect to x we get,
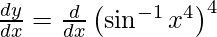
On using chain rule, we have
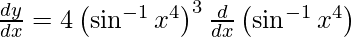
On using chain rule again, we have
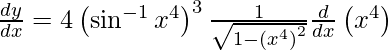
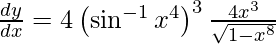
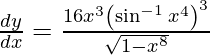
Question 48. Differentiate y =  with respect to x.
with respect to x.
Solution:
We have,
y = 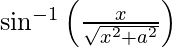
On differentiating y with respect to x we get,
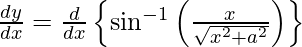
On using chain rule and quotient rule, we get
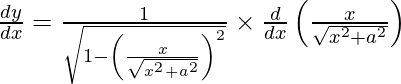
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{1}{\sqrt{1 - \left( \frac{x}{\sqrt{x^2 + a^2}} \right)^2}} \times \left[ \frac{\left( x^2 + a^2 \right)^\frac{1}{2} \frac{d}{dx}\left( x \right) - x\frac{d}{dx} \left( x^2 + a^2 \right)^\frac{1}{2}}{\left[ \left( x^2 + a^2 \right)^\frac{1}{2} \right]^2} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fd243ac729476138b0a02a7cebdefb0d_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{\sqrt{x^2 + a^2}}{\sqrt{x^2 + a^2 - x^2}}\left[ \frac{\sqrt{x^2 + a^2} - \frac{x}{2\sqrt{x^2 + a^2}}\frac{d}{dx}\left( x^2 + a^2 \right)}{\left( x^2 + a^2 \right)} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b48b6614279e317f0e3502fd9dda063b_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{\sqrt{x^2 + a^2}}{a\left( x^2 + a^2 \right)}\left[ \sqrt{x^2 + a^2} - \frac{x}{2\sqrt{x^2 + a^2}} \times 2x \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8e60620ef317c49c6feaa067e9ffc8bc_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{\sqrt{x^2 + a^2}}{a\left( x^2 + a^2 \right)}\left[ \frac{x^2 + a^2 - x^2}{\sqrt{x^2 + a^2}} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-266a6f53176b8d7cf72d694baefb3ea8_l3.png)

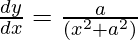
Question 49. Differentiate y = 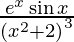 with respect to x.
with respect to x.
Solution:
We have,
y = 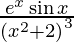
On differentiating y with respect to x we get,
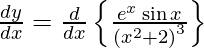
On using quotient rule, we get
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{\left( x^2 + 2 \right)^3 \frac{d}{dx}\left( e^x \sin x \right) - e^x \sin x\frac{d}{dx} \left( x^2 + 2 \right)^3}{\left[ \left( x^2 + 2 \right)^3 \right]^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3bf1e0229559953897218acad82bddd5_l3.png)
On using product rule, we get
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{\left( x^2 + 2 \right)^3 \left[ e^x \cos x + \sin x e^x \right] - e^x \sin x 3 \left( x^2 + 2 \right)^2 \left( 2x \right)}{\left( x^2 + 2 \right)^6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-480f8d344e5bfa98ab036d7f7f206d02_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{\left( x^2 + 2 \right)^3 \left[ e^x \cos x + e^x \sin x \right] - 6x e^x \sin x \left( x^2 + 2 \right)^2}{\left( x^2 + 2 \right)^6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-88174cbe5596a154778923b284f2bbed_l3.png)
![Rendered by QuickLaTeX.com \frac{d y}{d x} = \frac{\left( x^2 + 2 \right)^2 \left[ \left( x^2 + 2 \right)\left( e^x \cos x + e^x \sin x \right) - 6x e^x \sin x \right]}{\left( x^2 + 2 \right)^6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-342daa507ca80d9e0bfe256b270cf530_l3.png)
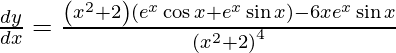

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...