Class 12 RD Sharma Solutions – Chapter 19 Indefinite Integrals – Exercise 19.24
Last Updated :
29 Apr, 2022
Question 1. ∫dx/(1-cotx)
Solution:
We have,
Let I=∫dx/(1-cotx)
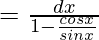
=∫sinx.dx/(sinx-cosx)
=(1/2)∫2sinx.dx/(sinx-cosx)
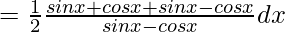
=(1/2)∫[(sinx+cosx)dx/(sinx-cosx)]+(1/2)∫dx
Let, sinx-cosx=z
Differentiating both sides we have
(cosx+sinx)dx=dz
=(1/2)Log|sinx-cosx|+(x/2)+C (Here C is integration constant)
Question 2. ∫dx/(1-tanx)
Solution:
We have,
Let I=∫dx/(1-tanx)
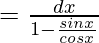
=∫cosx.dx/(cosx-sinx)
=(1/2)∫2cosx.dx/(cosx-sinx)
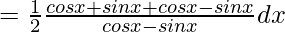
=(1/2)∫[(cosx+sinx)dx/(cosx-sinx)]+(1/2)∫dx
Let, cosx-sinx=z
Differentiating both sides we have
-(sinx+cosx)dx=dz
(sinx+cosx)dx=-dz
=(x/2)-(1/2)Log|cosx-sinx|+C (Here C is integration constant)
Question 3. ∫[(3+2cosx+4sinx)/(2sinx+cosx+3)]dx
Solution:
We have,
Let I=∫[(3+2cosx+4sinx)/(2sinx+cosx+3)]dx
Now substituting numerator
3+2cosx+4sinx=A(d/dx)(2sinx+cosx+3)+B(2sinx+cosx+3)+C
3+2cosx+4sinx=A(2cosx-sinx)+B(2sinx+cosx+3)+C
3+2cosx+4sinx=2Acosx-Asinx+2Bsinx+Bcosx+3B+C
3+2cosx+4sinx=(3B+C)+(2A+B)cosx+(2B-A)sinx
(3B+C)=3 (i)
(2A+B)=2 (ii)
(2B-A)=4 (iii)
On solving above equations,
A=0 ,B=2 ,C=-3

=2∫dx-∫3/(2sinx+cosx+3)
=I1-I2
I1=2∫dx
=2x
I2=∫3/(2sinx+cosx+3)
Substituting 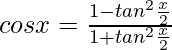 and
and 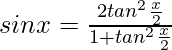
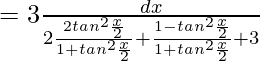
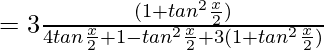
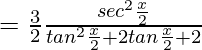
Let, tan(x/2)=z
Differentiating both sides,
(1/2)sec2(x/2)dx=dz
=3∫dz/(z2+2z+2)
=3∫dz/(z2+2z+1+1)
=3∫dz/{(z+1)2+12}
=3tan-1(z+1)
Putting the value of z
=3tan-1(tanx/2+1)
I2=3tan-1(tanx/2+1)
I=I1-I2
=2x-3tan-1(tanx/2+1)+C (Here C is integration constant)
Question 4. ∫dx/(p+qtanx)
Solution:
We have,
Let I=∫dx/(p+qtanx)
=∫[cosx/(pcosx+qsinx)]dx
Now substituting numerator
cosx=A(d/dx)(pcosx+qsinx)+B(pcosx+qsinx)+C
cosx=A(-psinx+qcosx)+B(pcosx+qsinx)+C
cosx=sinx(Bq-Ap)+cosx(Bp+Aq)+C
On comparing both sides,
C=0,
Bp+Aq=1,
Bq-Ap=0,
Solving above equation,
A=q/(p2+q2) and B=p/(p2+q2)
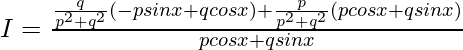 [Tex]I=∫\frac{\frac{q}{p^2+q^2}(-psinx+qcosx)+\frac{p}{p^2+q^2}(pcosx+qsinx)}{pcosx+qsinx}dx[/Tex]
[Tex]I=∫\frac{\frac{q}{p^2+q^2}(-psinx+qcosx)+\frac{p}{p^2+q^2}(pcosx+qsinx)}{pcosx+qsinx}dx[/Tex]
I=I1+I2
I1=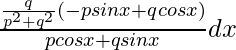
=q/(p2+q2)log|pcosx+qsinx|
I2=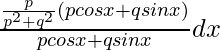
=px/(p2+q2)
I=q/(p2+q2)log|pcosx+qsinx|+px/(p2+q2)+C (Here C is integration constant)
Question 5. ∫[(5cosx+6)/(2cosx+sinx+3)]dx
Solution:
We have,
Let I=∫[(5cosx+6)/(2cosx+sinx+3)]dx
Now substituting numerator
5cosx+6=A(d/dx)(2cosx+sinx+3)+B(2cosx+sinx+3)+C
5cosx+6=A(-2sinx+cosx)+B(2cosx+sinx+3)+C
5cosx+6=sinx(B-2A)+cosx(2B+A)+3B+C
On comparing both sides,
3B+C=6,
2B+A=5,
B-2A=0,
Solving above equation,
A=1, B=2 and c=0
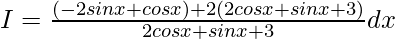
I=I1+I2
I1=∫[(-2sinx+cosx)/(2cosx+sinx+3)]dx
I1=log|2cosx+sinx+3|
I2=2∫dx
I2=2x
I=log|2cosx+sinx+3|+2x+C (Here C is integration constant)
Question 6. ∫[(2sinx+3cosx)/(3sinx+4cosx)]dx
Solution:
We have,
Let I=∫[(2sinx+3cosx)/(3sinx+4cosx)]dx
Now substituting numerator
2sinx+3cosx=A(d/dx)(3sinx+4cosx)+B(3sinx+4cosx)+C
2sinx+3cosx=A(3cosx-4sinx)+B(3sinx+4cosx)+C
2sinx+3cosx=sinx(3B-4A)+cosx(4B+3A)+3B+C
On comparing both sides,
3B-4A=2,
4B+3A=3,
Solving above equation,
A=1/25, B=18/25 and C=0
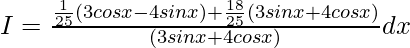
I=I1+I2
I1=(1/25)∫[(3cosx-4sinx)/(3sinx+4cosx)]dx
I1=(1/25)log|3sinx+4cosx|
I2=(18/25)∫dx
I2=(18x/25)
I=(1/25)log|3sinx+4cosx|+(18x/25)+C (Here C is integration constant)
Question 7. ∫dx/(3+4cotx)
Solution:
We have,
Let I=∫dx/(3+4cotx)
=∫[(sinx)/(3sinx+4cosx)]dx
Now substituting numerator
sinx=A(d/dx)(3sinx+4cosx)+B(3sinx+4cosx)+C
sinx=A(3cosx-4sinx)+B(3sinx+4cosx)+C
sinx=sinx(3B-4A)+cosx(4B+3A)+3B+C
On comparing both sides,
3B-4A=1,
4B+3A=0,
Solving above equation,
A=-4/25, B=3/25 and C=0
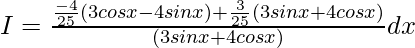
I=I1+I2
I1=(-4/25)∫[(3cosx-4sinx)/(3sinx+4cosx)]dx
I1=(-4/25)log|3sinx+4cosx|
I2=(3/25)∫dx
I2=(3x/25)
I=(3x/25)-(4/25)log|3sinx+4cosx|+(18x/25)+C (Here C is integration constant)
Question 8. ∫[(2tanx+3)/(3tanx+4)]dx
Solution:
We have,
Let I=∫[(2tanx+3)/(3tanx+4)]dx
=∫[(2sinx+3cosx)/(3sinx+4cosx)]dx
Now substituting numerator
2sinx+3cosx=A(d/dx)(3sinx+4cosx)+B(3sinx+4cosx)+C
2sinx+3cosx=A(3cosx-4sinx)+B(3sinx+4cosx)+C
2sinx+3cosx=sinx(3B-4A)+cosx(4B+3A)+C
On comparing both sides,
3B-4A=2,
4B+3A=3,
Solving above equation,
A=1/25, B=18/25 and C=0
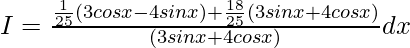
I=I1+I2
I1=(1/25)∫[(3cosx-4sinx)/(3sinx+4cosx)]dx
I1=(1/25)log|3sinx+4cosx|
I2=(18/25)∫dx
I2=(18x/25)
I=(1/25)log|3sinx+4cosx|+(18x/25)+C (Here C is integration constant)
Question 9. ∫dx/(4+3tanx)
Solution:
We have,
Let I=∫dx/(4+3tanx)
=∫[(cosx)/(4cosx+3sinx)]dx
Now substituting numerator
cosx=A(d/dx)(3sinx+4cosx)+B(3sinx+4cosx)+C
cosx=A(3cosx-4sinx)+B(3sinx+4cosx)+C
cosx=sinx(3B-4A)+cosx(4B+3A)+C
On comparing both sides,
3B-4A=0,
4B+3A=3,
Solving above equation,
A=3/25, B=4/25 and C=0
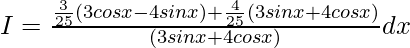
I=I1+I2
I1=(3/25)∫[(3cosx-4sinx)/(3sinx+4cosx)]dx
I1=(3/25)log|3sinx+4cosx|
I2=(4/25)∫dx
I2=(4x/25)
I=(3/25)log|3sinx+4cosx|+(4x/25)+C (Here C is integration constant)
Question 10. ∫[(8cotx+1)/(3cotx+2)]dx
Solution:
We have,
Let I=∫[(8cotx+1)/(3cotx+2)]dx
=∫[(8cosx+sinx)/(3cosx+2sinx)]dx
Now substituting numerator
8cosx+sinx=A(d/dx)(3cosx+2sinx)+B(3cosx+2sinx)+C
8cosx+sinx=A(-3sinx+2cosx)+B(3cosx+2sinx)+C
8cosx+sinx=sinx(2B-3A)+cosx(3B+2A)+C
On comparing both sides,
2B-3A=1,
3B+2A=3,
Solving the above equation,
A=1, B=2 and C=0
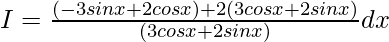
I=I1+I2
I1=∫[(-3sinx+2cosx)/(3cosx+2sinx)]dx
I1=log|3cosx+2sinx|
I2=2∫dx
I2=2x
I=log|3cosx+2sinx|+2x+C (Here C is integration constant)
Question 11. ∫[(4sinx+5cosx)/(5sinx+4cosx)]dx
Solution:
We have,
Let I=∫[(4sinx+5cosx)/(5sinx+4cosx)]dx
Now substituting numerator
4sinx+5cosx=A(d/dx)(5sinx+4cosx)+B(5sinx+4cosx)+C
4sinx+5cosx=A(5cosx-4sinx)+B(5sinx+4cosx)+C
4sinx+5cosx=sinx(5B-4A)+cosx(4B+5A)+C
On comparing both sides,
5B-4A=4,
4B+5A=5,
Solving the above equation,
A=9/41, B=40/41 and C=0
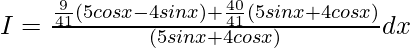
I=I1+I2
I1=(9/41)∫[(5cosx-4sinx)/(5sinx+4cosx)]dx
I1=(9/41)log|5sinx+4cosx|
I2=(40/41)∫dx
I2=(40x/41)
I=(9/41)log|5sinx+4cosx|+(40x/41)+C (Here C is integration constant)
Share your thoughts in the comments
Please Login to comment...