Class 12 RD Sharma Solutions- Chapter 19 Indefinite Integrals – Exercise 19.7
Last Updated :
13 Jan, 2021
Integrate the following integrals:
Question 1. ∫sin4x cos7x dx
Solution:
Let I= 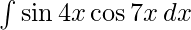
We know,
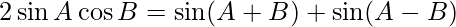
Applying this formula to the given question we get
I=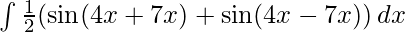
= 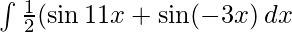
=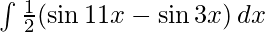
![Rendered by QuickLaTeX.com [\because \sin(-\theta)=-\sin\theta]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-48ab2bc69689063785cbf5218f846fa1_l3.png)
=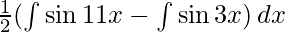
We know,
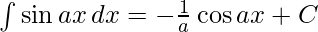
Applying this formula to the given question we get
I= 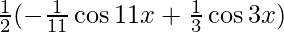
 I=
I= 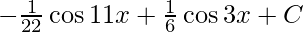
Question 2. ∫ cos3x cos4x dx
Solution:
Let I= 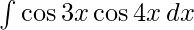
Multiplying and dividing the equation by 2,we get
I=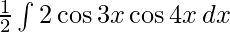
We know,
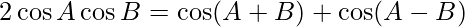
Applying this formula to the given question we get
I=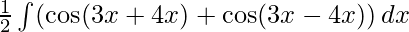
=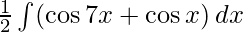
![Rendered by QuickLaTeX.com [\because \cos(-\theta)=\cos\theta]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c4acf5af31127cb5073e131eb6c4023f_l3.png)
We know,
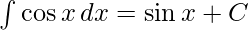 and
and 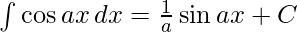
Applying these formulas to the given question we get
I=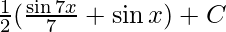
 I=
I=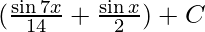
Question 3. ∫ cosmx cosnx dx, m≠n
Solution:
Let I= 
Multiplying and dividing the equation by 2,we get
I=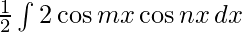
We know,
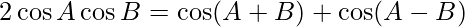
Applying this formula to the given question we get
I=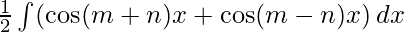
We know,
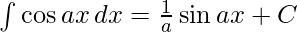
Applying these formulas to the given question we get
 I=
I=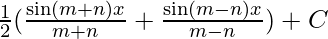
Question 4. ∫ sinmx cosnx dx, m≠n
Solution:
Let I=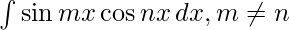
Multiplying and dividing the equation by 2,we get
I=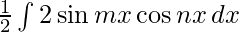
We know,
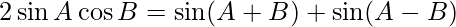
Applying this formula to the given question we get
I=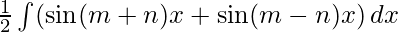
We know,
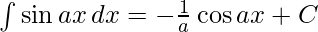
Applying these formulas to the given question we get
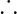 I=
I= 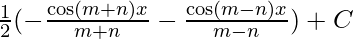
Share your thoughts in the comments
Please Login to comment...