Class 12 RD Sharma Solutions – Chapter 19 Indefinite Integrals – Exercise 19.1
Last Updated :
02 Feb, 2021
Question 1. Integrate the following integrals with respect to x:
(i) ∫ x4 dx
Solution:
∫ x4 dx = x4+1/(4+1) + Constant
= x5/5 + C
(ii) ∫ x5/4 dx
Solution:
∫ x5/4 dx = x5/4 + 1/(5/4 +1) + Constant
= 4/9 x9/4 + C
(iii) ∫ 1/x5 dx
Solution:
∫ 1/x5 dx = ∫ x-5 dx
= x-5+1/(-5+1) + Constant
= x-4/(-4)+ C
= -1/(4x4) + C
(iv) ∫ 1/x3/2 dx
Solution:
∫ x-3/2 dx = x-3/2 + 1/(-3/2 +1) + Constant
= x-1/2/(-1/2) + C
= -2/(√x)+ C
(v) ∫ 3x dx
Solution:
∫ 3x dx = 3x/log3 + Constant
(vi) ∫ 1/x2/3 dx
Solution:
∫ 1/x2/3 dx = ∫ x-2/3 dx
= x-2/3 + 1/(-2/3+1) + Constant
= x1/3/(1/3) + C
= 3x1/3 + C
(vii) ∫ 32log3 x dx
Solution:
∫ 32log3 x dx = 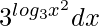
= ∫ x2 dx
= x2+1/(2+1) + Constant
= x3/3 + C
Question 2. Evaluate
(i) 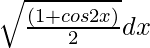
Solution:
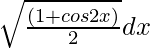
= 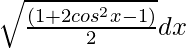
We know, cos 2x = 2cos2 x – 1
=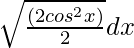
= ∫cos x dx
= sin x + Constant
(ii)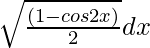
Solution:
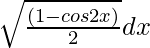
= 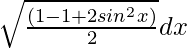
We know, cos 2x = 1 – 2sin2 x
= 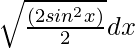
= ∫ sin x dx
= -cos x + Constant
Question 3. Evaluate 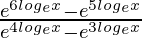
Solution:
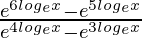 dx
dx
= 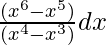
We know, e loge x = x
= 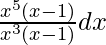
= ∫ x2 dx
= x2+1/2+1 + Constant
= x3/3 + C
Question 4. Evaluate: 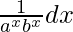
Solution:
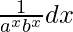 = ∫ a-x b-x dx
= ∫ a-x b-x dx
= ∫ (ab)-x dx
= (ab)-x/loge (ab)-1 + Constant
= -a-x b-x/loge (ab) + C
or
= -a-x b-x/ ln(ab) + C
Question 5. Evaluate
(i) 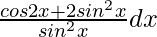
Solution:
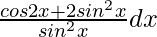
= 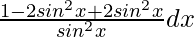
We know, cos 2x = 1 – 2sin2 x
= ∫ 1/sin2x dx = ∫ cosec2x dx
= -cot x + Constant
(ii) 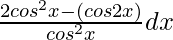
Solution:
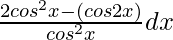
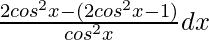
We know, cos 2x = 2cos2 x – 1
= ∫ 1/cos2 x dx = ∫ sec2 x dx
= tan x + Constant
Question 6. Evaluate: ∫ elog√x /x dx
Solution:
∫ eloge √x /x dx = ∫√x/x dx
= ∫ x-1/2 dx = x-1/2 + 1/(-1/2 + 1) + Constant
= x1/2 /(1/2) + C
= 2√x + C
Share your thoughts in the comments
Please Login to comment...