Class 12 RD Sharma Solutions – Chapter 11 Differentiation – Exercise 11.7 | Set 1
Last Updated :
20 May, 2021
Question 1. Find  , when: x = at2 and y = 2at
, when: x = at2 and y = 2at
Solution:
Given that x = at2, y = 2at
So,
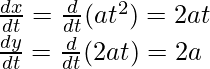
Therefore,
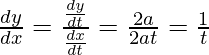
Question 2. Find  , when: x = a(θ + sinθ) and y = a(1 – cosθ)
, when: x = a(θ + sinθ) and y = a(1 – cosθ)
Solution:
Here,
x = a(θ + sinθ)
Differentiating it with respect to θ,
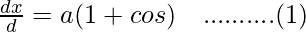
and,
y = a(1 – cosθ)
Differentiate it with respect to θ,

Using equation (1) and (2),
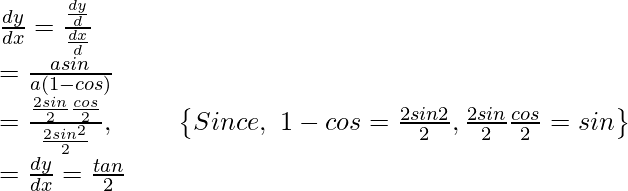
Question 3. Find  , when: x = acosθ and y = bsinθ
, when: x = acosθ and y = bsinθ
Solution:
Then x = acosθ and y = bsinθ
Then,
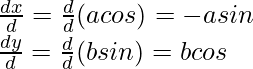
Therefore,
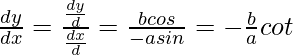
Question 4. Find  , when: x = aeΘ (sinθ -cosθ), y = aeΘ (sinθ +cosθ)
, when: x = aeΘ (sinθ -cosθ), y = aeΘ (sinθ +cosθ)
Solution:
Here,
x = aeΘ (sinθ – cosθ)
Differentiating it with respect to θ,
![Rendered by QuickLaTeX.com \frac{dx}{dθ}=a[e^θ\frac{d}{dθ}(sinθ-cosθ)+(sinθ-cosθ)\frac{d}{dθ}(e^θ)]\\ =a[e^θ(cosθ+sinθ)+(sinθ-cosθ)e^θ]\\ \frac{dx}{dθ}=a[2e^θsinθ]\ \ \ \ \ \ .......(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2ae44003272bf3428cebf6561cbb74c4_l3.png)
And,
y = aeΘ(sinθ+cosθ)
Differentiating it with respect to θ
![Rendered by QuickLaTeX.com \frac{dy}{dθ}=a[e^θ\frac{d}{dθ}(sinθ+cosθ)+(sinθ+cosθ)\frac{d}{dθ}(e^θ)]\\ =a[e^θ(cosθ-sinθ)+(sinθ+cosθ)e^θ]\\ \frac{dx}{dθ}=a[2e^θcosθ]\ \ \ \ \ \ .......(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-322bbedc6e2f747634da1bbf9987f88e_l3.png)
Dividing equation (2) by equation (1)
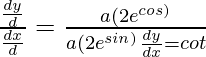
Question 5. Find  , when: x = bsin2θ and y = acos2θ
, when: x = bsin2θ and y = acos2θ
Solution:
Here,
x = bsin2θ and y = acos2θ
Then,
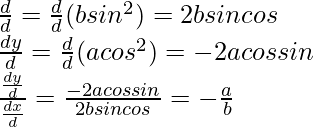
Question 6. Find  , when: x = a(1 – cosθ) and y = a(θ +sinθ) at θ =
, when: x = a(1 – cosθ) and y = a(θ +sinθ) at θ =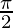
Solution:
Here,
x = a(1 – cosθ) and y = a(θ + sinθ)
Then,
![Rendered by QuickLaTeX.com \frac{dx}{dθ}=\frac{d}{dθ}[a(1-cosθ)]=asinθ\\ \frac{dy}{dθ}=\frac{d}{dθ}[a(θ +sinθ)]=a(1+cosθ)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7a39d173d5f8bc38c6edaad0629b8e58_l3.png)
Therefore,
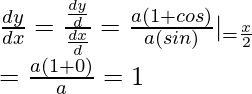
Question 7. Find  , when:
, when: 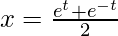 and
and
Solution:
Here,
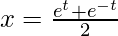
Differentiate it with respect to t,
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\frac{1}{2}\left[\frac{d}{dt}(e^t)+\frac{d}{dt}(e^{-t})\right]\\ =\frac{1}{2}\left[e^t+e^{-t}\frac{d}{dt}(e^{-t})\right]\\ \frac{dx}{dt}=\frac{1}{2}(e^t-e^{-t})=y\ \ \ ......(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f82afd089cd07a5a4bb21127dd523341_l3.png)
and,

Differentiating it with respect to t,
![Rendered by QuickLaTeX.com \frac{dy}{dt}=\frac{1}{2}\left[\frac{d}{dt}(e^t)-\frac{d}{dt}(e^{-t})\right]\\ =\frac{1}{2}\left[e^t-e^{-t}\frac{d}{dt}(e^{-t})\right]\\ \frac{dx}{dt}=\frac{1}{2}(e^t+e^{-t})=x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0374781882627f150ffd3dce4d85518_l3.png)
![Rendered by QuickLaTeX.com \frac{dy}{dt}=\frac{1}{2}\left[\frac{d}{dt}(e^t)-\frac{d}{dt}(e^{-t})\right]\\ =\frac{1}{2}\left[e^t-e^{-t}\frac{d}{dt}(e^{-t})\right]\\ \frac{dx}{dt}=\frac{1}{2}(e^t+e^{-t})=x\ \ \ \ .....(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aaef7944d5445fbd5afcc836606061d5_l3.png)
Dividing equation (2) and (1)
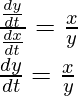
Question 8. Find  , when:
, when: 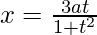 and
and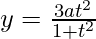
Solution:
Here,
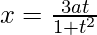
Differentiating it with respect to t using quotient rule,
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\left[\frac{(1+t^2)\frac{d}{dt}(3at)-3at\frac{d}{dt}(1+t^2)}{(1+t^2)^2}\right]\\ =\left[\frac{(1+t^2)(3a)-3at(2t)}{(1+t^2)^2}\right]\\ =\left[\frac{3a+3at^2-6at^2}{(1+t^2)^2}\right]\\ =\left[\frac{3a-3at^2}{(1-t^2)^2}\right]\\ \frac{dx}{dt}=\frac{3a(1-t^2)}{(1+t^2)^2}\ \ \ \ ....(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-66b0fcdb192f11a038cebecc2448593d_l3.png)
and,
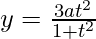
Differentiating it with respect to t using quotient rule,
![Rendered by QuickLaTeX.com \frac{dy}{dt}=\left[\frac{(1+t^2)\frac{d}{dt}(3at^2)-3at^2\frac{d}{dt}(1+t^2)}{(1+t^2)^2}\right]\\ =\left[\frac{(1+t^2)(6at)-(3at^2)(2t)}{(1+t^2)^2}\right]\\ =\left[\frac{6at+6at^3-6at^3}{(1+t^2)^2}\right]\\ \frac{dy}{dt}=\frac{6at}{(1+t^2)^2}\ \ \ \ ....(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-193c0a0b50b7cc8a3f19caffc740c1f9_l3.png)
Dividing equation (2) by (1)
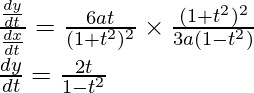
Question 9. If x and y are connected parametrically by the equation, without eliminating the parameter, find when: x = a(cosθ +θsinθ), y = a(sinθ -θcosθ)
when: x = a(cosθ +θsinθ), y = a(sinθ -θcosθ)
Solution:
The given equations are
x = a(cosθ +θ sinθ) and y = a(sinθ -θcosθ)
Then,
![Rendered by QuickLaTeX.com \frac{dx}{dθ}=a\left[\frac{d}{dθ}cosθ +\frac{d}{dθ}(θ sinθ)\right]\\ =a\left[-sinθ +θ \frac{d}{dθ}(sinθ)+sinθ \frac{d}{dθ}(θ)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ba02a50e8787421b2adfe6e2b974fb2_l3.png)
= a[-sinθ + θcosθ + sinθ] = aθcosθ
![Rendered by QuickLaTeX.com \frac{dy}{dθ}=a\left[\frac{d}{dθ}sinθ +\frac{d}{dθ}(θ cosθ)\right]\\ =a\left[cosθ -\{θ \frac{d}{dθ}(cosθ)+cosθ \frac{d}{dθ}(θ)\}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bae259f6ef8efa5e670376cde4041048_l3.png)
= a[cosθ +θsinθ -cosθ]
= aθsinθ
Therefore,
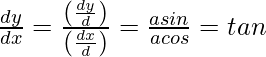
Question 10. Find  , when:
, when: 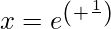 and
and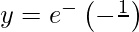
Solution:
Here,

Differentiating it with respect to θ using product rule,
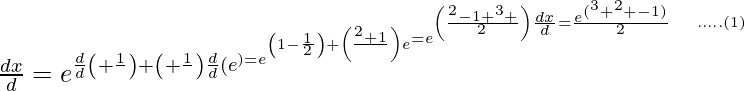
and,
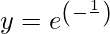
Differentiating it with respect to θ using product rule and chain rule
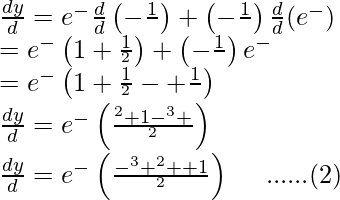
Share your thoughts in the comments
Please Login to comment...