Class 12 RD Sharma Solutions – Chapter 11 Differentiation – Exercise 11.3 | Set 3
Last Updated :
08 May, 2021
Question 33. Differentiate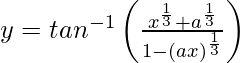 with respect to x.
with respect to x.
Solution:
We have,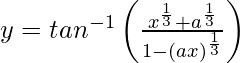
=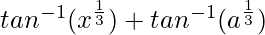
Differentiating with respect to x, we get,
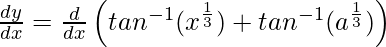
=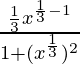
=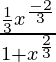
=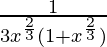
Question 34. Differentiate with respect to x.
with respect to x.
Solution:
We have,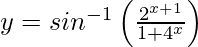
On putting 2x = tan θ, we get,
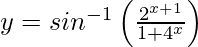
=
=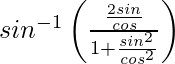
=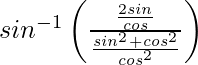
=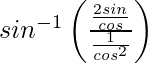
=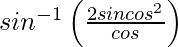
=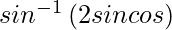
=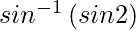
= 2θ
= 2 tan−1 (2x)
Differentiating with respect to x, we get,
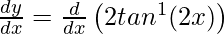
=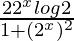
=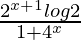
Question 35. If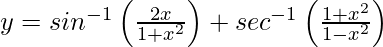 , 0 < x < 1, prove that
, 0 < x < 1, prove that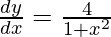 .
.
Solution:
We have,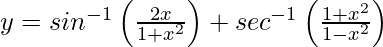
=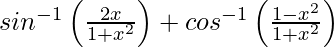
On putting x = tan θ, we get,
y =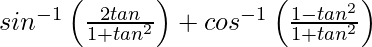
=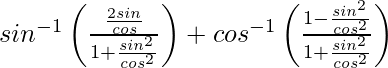
=
=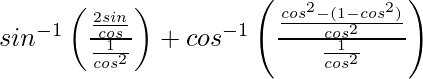
=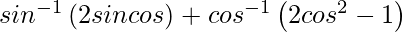
=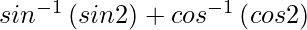
Now, 0 < x < 1
=> 0 < tan θ < 1
=> 0 < θ < π/4
=> 0 < 2θ < π/2
So, y = 2θ + 2θ
= 4θ
= 4 tan−1 x
Now, L.H.S. =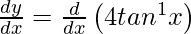
=
= R.H.S.
Hence proved.
Question 36. If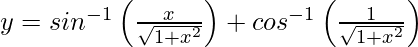 , 0 < x < ∞, prove that
, 0 < x < ∞, prove that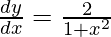 .
.
Solution:
We have,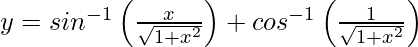
On putting x = tan θ, we get,
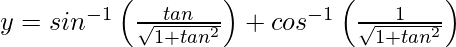
=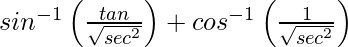
=
=
=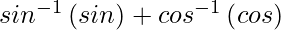
Now, 0 < x < ∞
=> 0 < tan θ < ∞
=> 0 < θ < π/2
So, y = θ + θ
= 2θ
= 2 tan−1 x
Now, L.H.S. =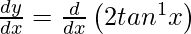
=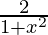
= R.H.S.
Hence proved.
Question 37 Differentiate the following with respect to x :
(i) cos−1 (sin x)
Solution:
We have, y = cos−1 (sin x)
=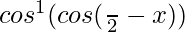
=
Differentiating with respect to x, we get,

= 0 − 1
= −1
(ii) 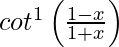
Solution:
We have, y =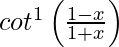
On putting x = tan θ, we get,
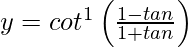
=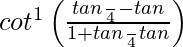
=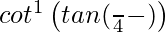
=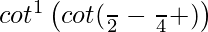
=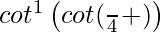
=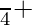
=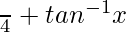
Differentiating with respect to x, we get,

= 0 +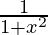
=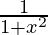
Question 38. Differentiate![Rendered by QuickLaTeX.com y=cot^{-1}\left[\frac{\sqrt{1+sinx}+\sqrt{1-sinx}}{\sqrt{1+sinx}-\sqrt{1-sinx}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9015b75f6699eacdbfd989ff26cc9c13_l3.png) , 0 < x < π/2 with respect to x.
, 0 < x < π/2 with respect to x.
Solution:
We have,![Rendered by QuickLaTeX.com y=cot^{-1}\left[\frac{\sqrt{1+sinx}+\sqrt{1-sinx}}{\sqrt{1+sinx}-\sqrt{1-sinx}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b7d294d11dd6b91899328823f590ff4b_l3.png)
=![Rendered by QuickLaTeX.com cot^{-1}\left[\frac{(\sqrt{1+sinx}+\sqrt{1-sinx})^2}{(\sqrt{1+sinx}-\sqrt{1-sinx})(\sqrt{1+sinx}+\sqrt{1-sinx})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e323173fef854d3403ed7f0ab2551b6c_l3.png)
=![Rendered by QuickLaTeX.com cot^{-1}\left[\frac{1+sinx+1-sinx+2(\sqrt{1+sinx})(\sqrt{1-sinx})}{1+sinx-1+sinx}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4568aa3e831767a3be539485a4303b84_l3.png)
=![Rendered by QuickLaTeX.com cot^{-1}\left[\frac{2+2(\sqrt{1-sin^2x})}{2sinx}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-05fbdc35228fb3e5feb427b480860719_l3.png)
=![Rendered by QuickLaTeX.com cot^{-1}\left[\frac{2+2cosx}{2sinx}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-295dbde2608a3ed9b9a32607b1ce481e_l3.png)
=![Rendered by QuickLaTeX.com cot^{-1}\left[\frac{1+cosx}{sinx}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e376fb2baf3b4dcf8b132bdd89eaee7e_l3.png)
=![Rendered by QuickLaTeX.com cot^{-1}\left[\frac{2cos^2\frac{x}{2}}{2sin\frac{x}{2}cos\frac{x}{2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-af4eec886c5c4caaae06798e0e77ad4c_l3.png)
=![Rendered by QuickLaTeX.com cot^{-1}\left[cot\frac{x}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0d5f8e701ae0be88f9208f92ada56649_l3.png)
=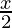
Differentiating with respect to x, we get,
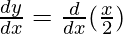
=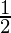
Question 39. If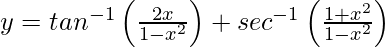 , x > 0, prove that
, x > 0, prove that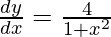 .
.
Solution:
We have,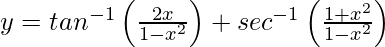
=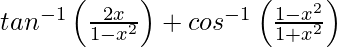
On putting x = tan θ, we get,
y =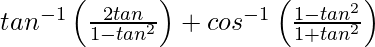
=
=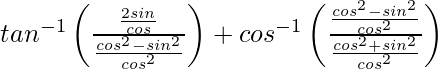
=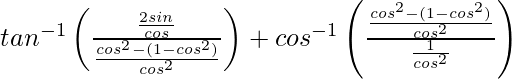
=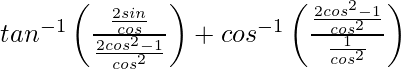
=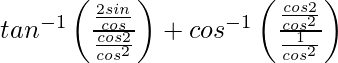
=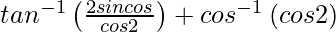
=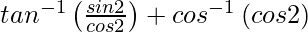
=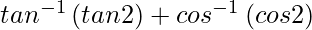
Here, 0 < x < ∞
=> 0 < tan θ < ∞
=> 0 < θ < π/2
=> 0 < 2θ < π
So, y = 2θ + 2θ
= 4θ
= 4 tan−1 x
Now, L.H.S. =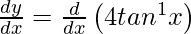
=
= R.H.S.
Hence proved.
Question 40. If , x > 0, find
, x > 0, find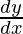 .
.
Solution:
We have,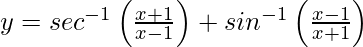
=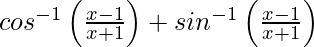
=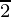
Differentiating with respect to x, we get,
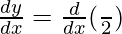
= 0
Question 41. If![Rendered by QuickLaTeX.com y=sin\left[2tan^{-1}\sqrt{(\frac{1-x}{1+x})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bb6ed5ceb9104cb290498f06714f900a_l3.png) , find
, find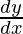 .
.
Solution:
We have,![Rendered by QuickLaTeX.com y=sin\left[2tan^{-1}\sqrt{(\frac{1-x}{1+x})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-00b58407d2b8fa8b4a29a0d56f828d49_l3.png)
On putting x = cos 2θ, we get,
![Rendered by QuickLaTeX.com y=sin\left[2tan^{-1}\sqrt{(\frac{1-cos2θ}{1+cos2θ})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-56991ceab024f6cb2b50e16041ad45a3_l3.png)
=![Rendered by QuickLaTeX.com sin\left[2tan^{-1}\sqrt{(\frac{2sin^2θ}{2cos^2θ})}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-386f3373d40772239850276da57be226_l3.png)
=![Rendered by QuickLaTeX.com sin\left[2tan^{-1}(\sqrt{tan^2θ})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-30f14e1849bb606bb97b1bc872da96bf_l3.png)
=![Rendered by QuickLaTeX.com sin\left[2tan^{-1}(tanθ)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-db42c36685ea00a7d254b162e2008e62_l3.png)
=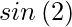
=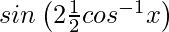
=
=
=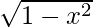
Differentiating with respect to x, we get,

=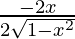
=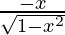
Question 42. If 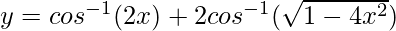 , 0 < x < 1/2, find
, 0 < x < 1/2, find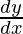 .
.
Solution:
We have,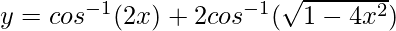
On putting 2x = cos θ, we get,
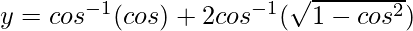
=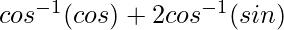
=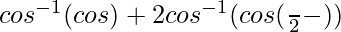
Now, 0 < x < 1/2
=> 0 < 2x < 1
=> 0 < cos θ < 1
=> 0 < θ < π/2
and 0 > −θ > −π/2
=> π/2 > (π/2 −θ) > 0
So, y =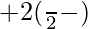
= π − θ
= π − cos−1 (2x)
Differentiating with respect to x, we get,
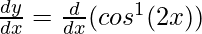
=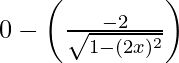
=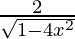
Question 43. If the derivative of tan−1 (a + bx) takes the value of 1 at x = 0, prove that 1 + a2 = b.
Solution:
We have, y = tan−1 (a + bx)
Differentiating with respect to x, we get,
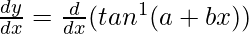
=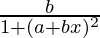
At x = 0, we have,
=> = 1
= 1
=>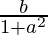 = 1
= 1
=> 1 + a2 = b
Hence proved.
Question 44. If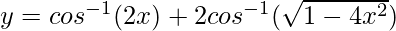 , −1/2 < x < 0, find
, −1/2 < x < 0, find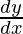 .
.
Solution:
We have,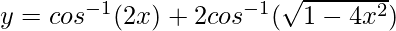
On putting 2x = cos θ, we get,
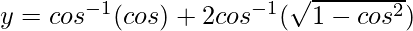
=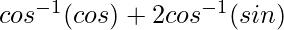
=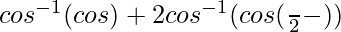
Now, −1/2 < x < 0
=> −1 < 2x < 0
=> −1 < cos θ < 0
=> π/2 < θ < π
and −π/2 > −θ > −π
=> 0 > (π/2 −θ) > −π/2
So, y =
= −π + 3θ
= −π + 3 cos−1 (2x)
Differentiating with respect to x, we get,

= 0 +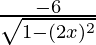
=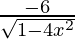
Question 45. If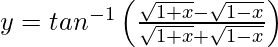 , find
, find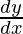 .
.
Solution:
We have,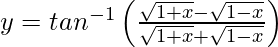
On putting x = cos 2θ, we get,
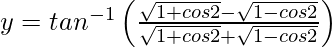
=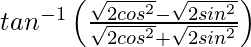
=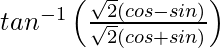
=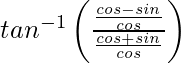
=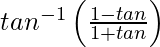
=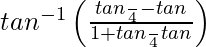
=
=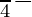
=
Differentiating with respect to x, we get,
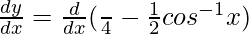
= 0 −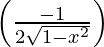
=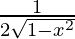
Question 46. If 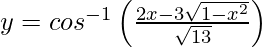 , find
, find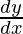 .
.
Solution:
We have,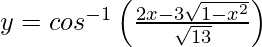
On putting x = cos θ, we get,
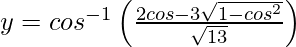
=
=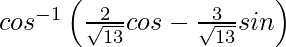
Let
=> sin Ø =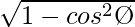
=> sin Ø =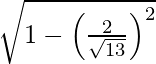
=> sin Ø =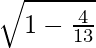
=> sin Ø =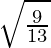
=> sin Ø =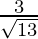
So, y =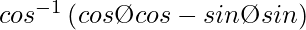
=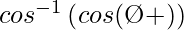
= Ø + θ
=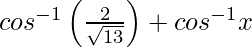
Differentiating with respect to x, we get,
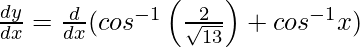
= 0 +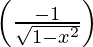
=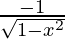
Question 47. Differentiate![Rendered by QuickLaTeX.com y=sin^{-1}\left[\frac{2^{x+1}×3^x}{1+(36)^x}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b8746d78a8494be45d3ac06c2f1e906a_l3.png) with respect to x.
with respect to x.
Solution:
We have,![Rendered by QuickLaTeX.com y=sin^{-1}\left[\frac{2^{x+1}×3^x}{1+(36)^x}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-533aaee9226d238c221cb8b05818a5b2_l3.png)
=![Rendered by QuickLaTeX.com sin^{-1}\left[\frac{2×2^x×3^x}{1+(36)^x}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5536f3412abdbe74534b319e8ea9975d_l3.png)
=![Rendered by QuickLaTeX.com sin^{-1}\left[\frac{2×6^x}{1+(6)^{2x}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f0ea6e243aa09eeebd514057cb08ec85_l3.png)
On putting 6x = tan θ, we get,
=![Rendered by QuickLaTeX.com sin^{-1}\left[\frac{2tanθ}{1+tan^2θ}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-86b7ede90aa834def69dfe5241996d43_l3.png)
=![Rendered by QuickLaTeX.com sin^{-1}\left[\frac{\frac{2sinθ}{cosθ}}{1+\frac{sin^2θ}{cos^2θ}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d24c4bb96cc1748918916bfac394f18_l3.png)
=![Rendered by QuickLaTeX.com sin^{-1}\left[\frac{\frac{2sinθ}{cosθ}}{\frac{cos^2θ+sin^2θ}{cos^2θ}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-18742e0c0322a1587ac817cd437ed921_l3.png)
=![Rendered by QuickLaTeX.com sin^{-1}\left[\frac{\frac{2sinθ}{cosθ}}{\frac{1}{cos^2θ}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a47897252e094680ce2b8a1701a32302_l3.png)
=![Rendered by QuickLaTeX.com sin^{-1}\left[{\frac{2sinθcos^2θ}{cosθ}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c69ca7c8ddce0a1b29b1b62fed3984b0_l3.png)
=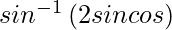
=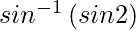
= 2θ
= 2 tan−1 (6x)
Differentiating with respect to x, we get,
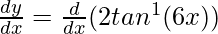
=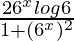
=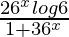
Share your thoughts in the comments
Please Login to comment...